对于几种基本凸起情形,下面通过示例进行载荷性分析。
情形1:自由平放的矩形盘,所有面承受同样的压力,即κ=1。
对应于此种情形的方程式(19.13)为
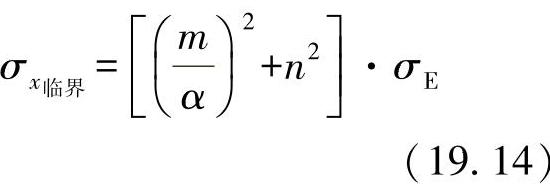
当m=n=1时,可引入凸起应力的最小值。由此可以得出:

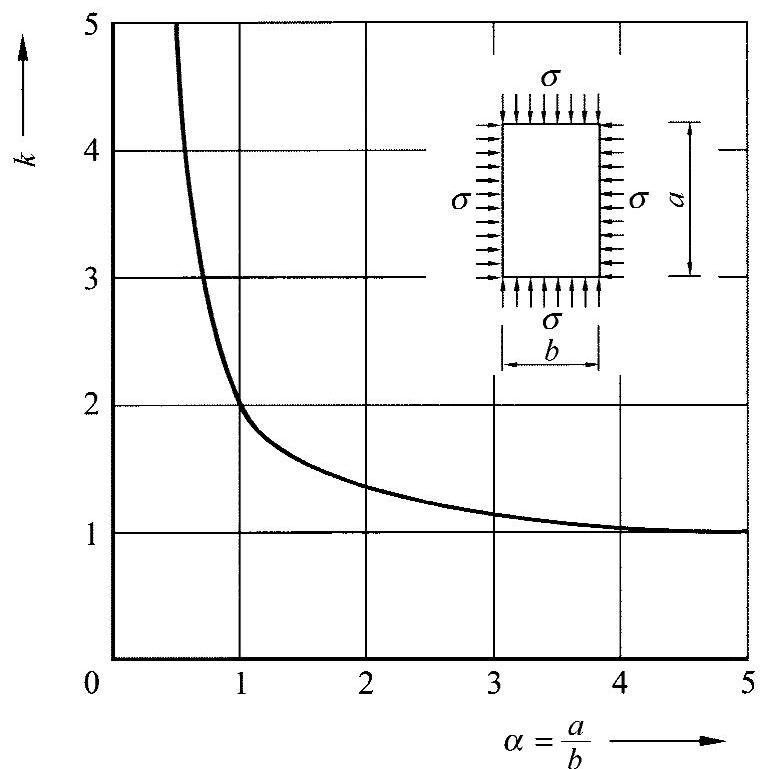
图19-3 矩形盘的凸起值[KOL 58]
也就是说,凸起值为:

图19-3所示为与盘的长宽比相关的凸起值的变化过程。
对于一个α=1的正方形盘,有k=2,即与平板条相比,该盘可承受两倍的欧拉应力。
情形2:自由平放的矩形盘,一端不受力,一端承受压力。
对应于前面的定义有κ=0,则凸起应力为
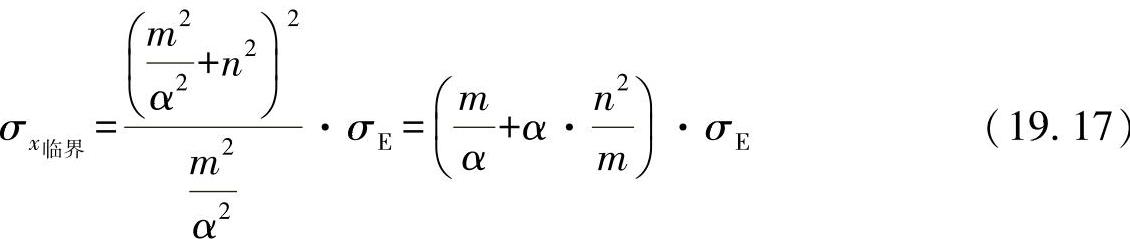
据此,可确定凸起值为

对凸起值还要做进一步的研究:凸起发生在最小凸起值时以及全序列m、n值情况下。对于一个任意的α,必须要找到kmin。这肯定是在n=1(即在横向只有一个预期的半波)的时候,由此可得出其他的半波:
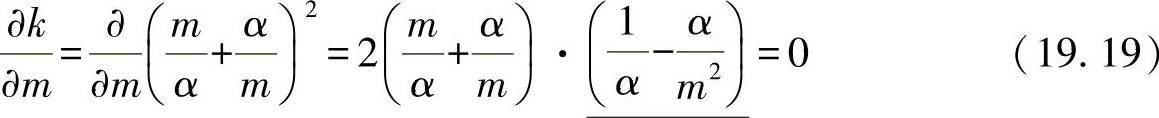
当第二个括号内的项消失时,该表达式可以为零,即:
m=α
由方程式(19.18)可得出:
kmin=4
与
σx临界=4·σE
因为根据前提条件,m与n应为全序列,则最小凸起值也只在全序列比例关系α下出现。即在相应的受载盘上,a侧是b侧的全序列倍数。凸起数字可表示b向的一个半波(n=1)和a向的m个半波,数字越多,α越大。
对于与此不同的比例α<1或者m<α<(m+1),则凸起值恒定大于k=4。特别是对于α<1,凸起值急剧增加。
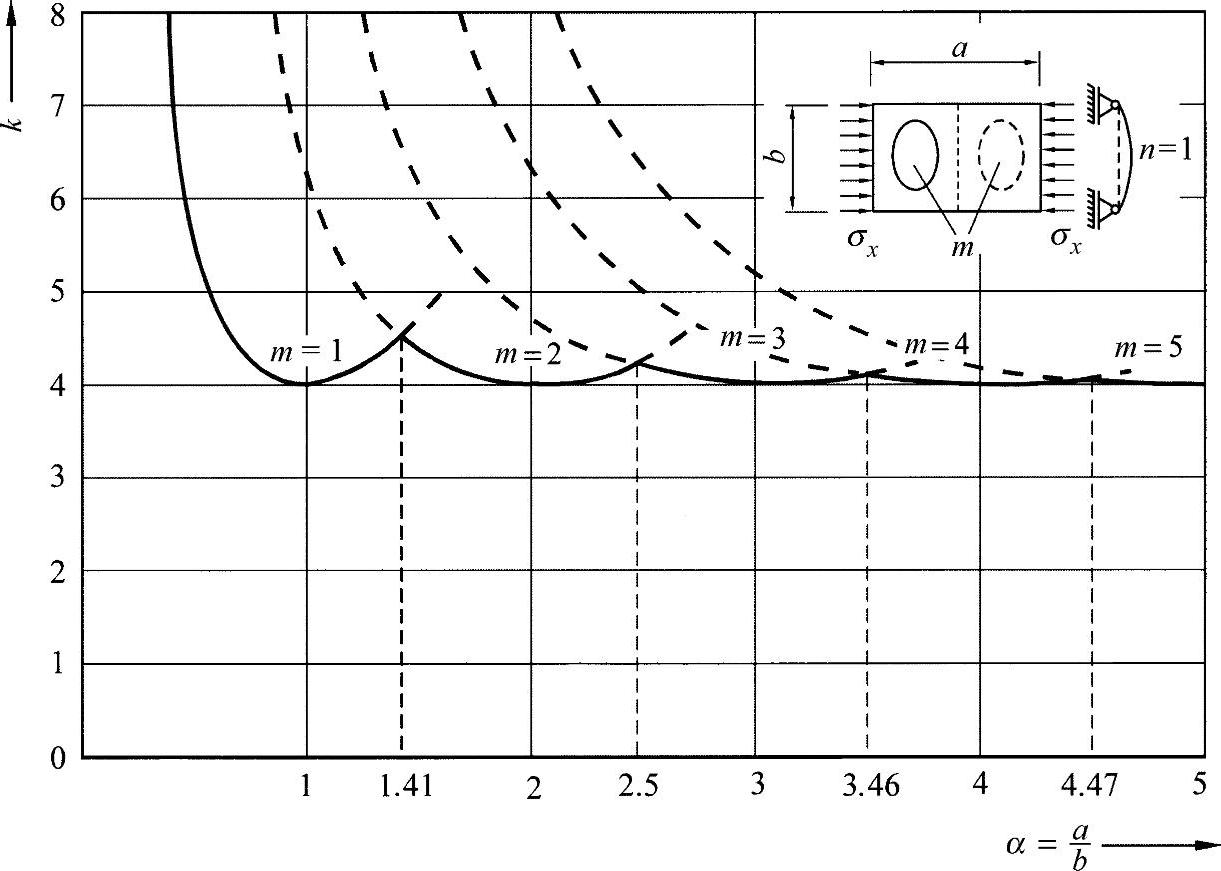
对于固定的n=1,根据方程式(19.18)求解凸起值,则可得出如图19-4所示的典型的吊挂曲线。第一个临界情形为正方形盘m=n=1,由此得出凸起应力:
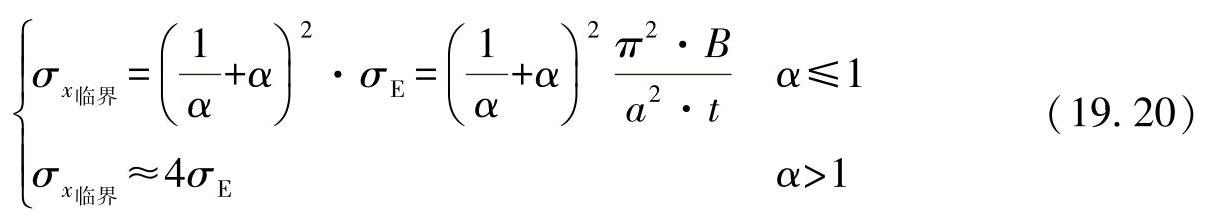
 (https://www.xing528.com)
(https://www.xing528.com)
图19-4 在单侧压力下矩形板的凸起值[KOL 58],铰接支座,下限为k=4
情形3:自由平放的矩形盘,a侧受拉,b侧受压。在这种情形中,特别突出的是一个小拉应力载荷的加固效果。
根据应力载荷作用有σy=-κ·σx,并由此有:
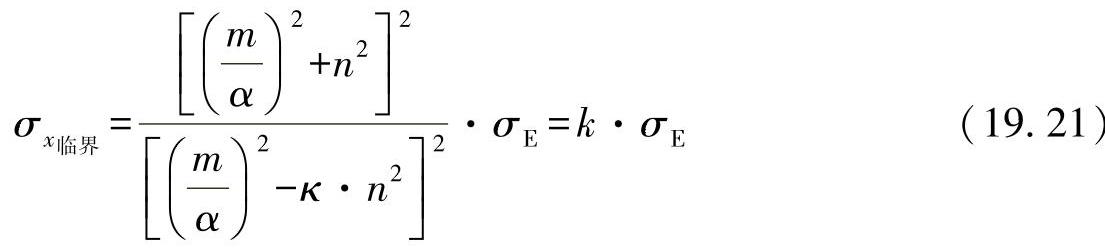
因为在上述的情形下,m与n事先无法确定,可由如下条件得出最小凸起值:
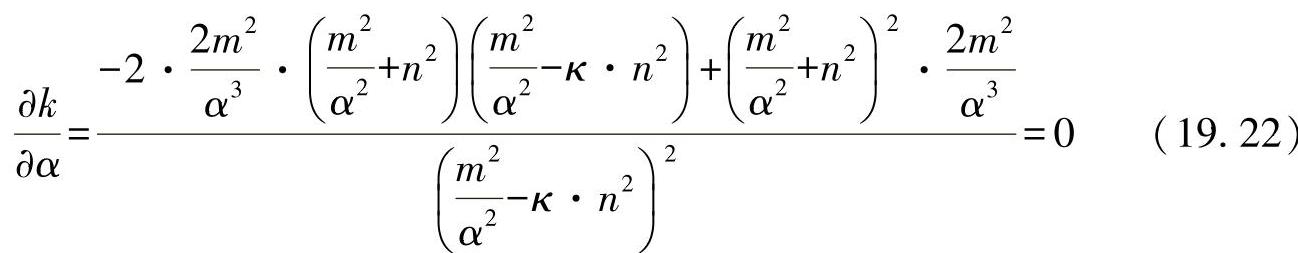
不过,该表达式只对于消失的数字可为零。通过转换可得出新的条件:
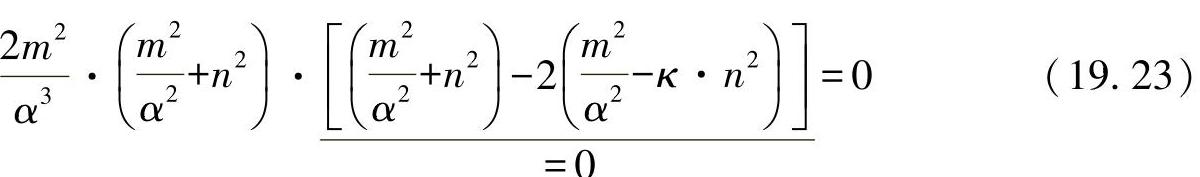
或者进一步得出减少后的条件:
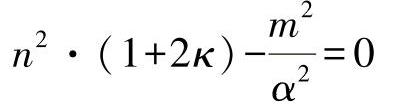
与 (19.24)
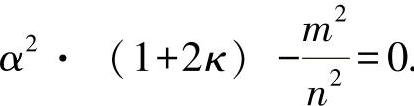
其解为

现在再将α值代入凸起值定义中,可有:
kmin=4n2(1+κ) (19.26)
就是说,现在最小凸起值不取决于半波数m,并且对n=1最小,即:
kmin/min=4(1+κ)
这里有:

由于在方程式(19.27)中,根值恒定大于1,对于m=1,须有α<1。由此可得,在x方向上,半波长度小于b的边长。随着应力比例κ的增加,半波长总是变小,而凸起值变大。只有当更长的侧面满足下述条件时,才有最小凸起值:
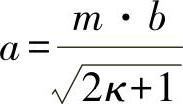
它大于所有其他边长a,特别是对于比例:
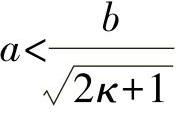
凸起值急剧上升。对于有更大边长的相反关系,则最小凸起值的偏差更小。对凸起值与边长比例的变化进行展开,则又可得到典型的吊挂曲线。图19-5所示的变化过程特别对应于应力比例κ=4的情形。
从图中可以看出,最小凸起值为kmin=20,出现在α=m/3时。对于一个α=1的正方形盘,在x向上的位置为m=3,即产生三个半波。
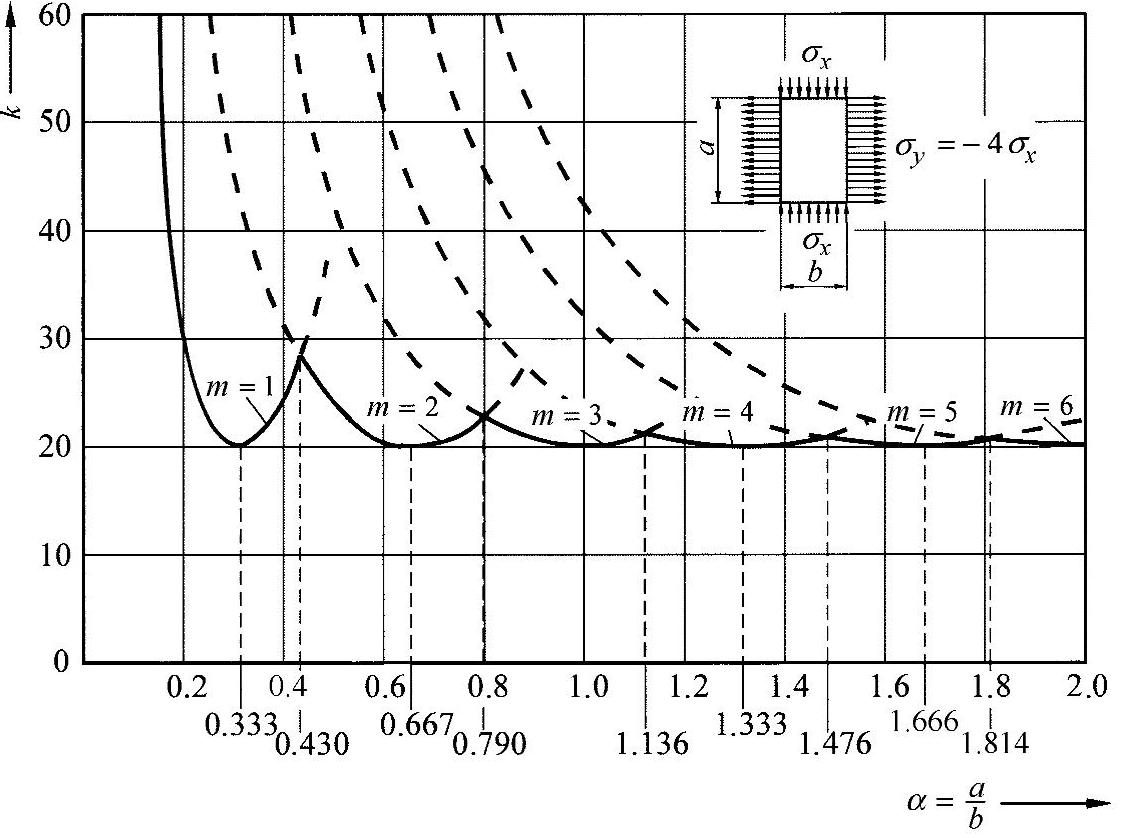
图19-5 在压与拉下对于比例κ=4的矩形板凸起值[KOL 58]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




