【摘要】：对于简单的凸起情形，上述微分方程可通过直接积分求解。下面利用一个所有面都承压的自由平放的矩形盘来说明这一方法。对上述表达式进行求导[2]：可求出微分方程的解为整理后为通过如下转换：可求出在边界上的应力载荷与凸起形状之间的关系。如果定义长宽比为α=a/b，则可以将式修改为其中，k为欧拉应力的倍数。σx的最小值为所求的临界凸起应力，对于一定的半波数，由该值可导出凸起值的最小值。凸起值通常采用列表的方式给出。
对于简单的凸起情形，上述微分方程可通过直接积分求解。下面利用一个所有面都承压的自由平放的矩形盘（图19-2）来说明这一方法。根据约定，在所有情形下，坐标系x、y方向应确定为：恒定有nx>ny。
根据计算的外载荷即可得出τxy=0，由此可计算出凸起方程为
图19-2 所有侧面都受压的矩形盘
为了简化起见，可进一步利用应力比例σy=κ·σx，则上述方程可改写为
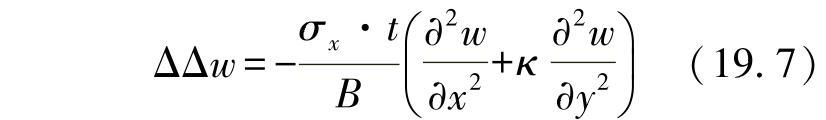
在无力矩作用的支座情形下，对这一微分方程类型直接积分，可得到如下的求解方程式：
该表达式基于如下假设，即边界按正弦半波翘曲。代入的序数m、n可为全序列：
m=1，2，3，… 与 n=1，2，3，…
因为它们规定了在盘侧面a与b上的半波数目。对上述表达式进行求导[2]：
(www.xing528.com)
可求出微分方程的解为
整理后为
通过如下转换：
可求出在边界上的应力载荷与凸起形状之间的关系。为了进一步得出压弯的类比结果，可将一个平板条的欧拉抗弯应力代入下面的方程：
该平板条两端为铰接支座，长度为b，宽度a=1。如果定义长宽比为α=a/b，则可以将式（19.11）修改为
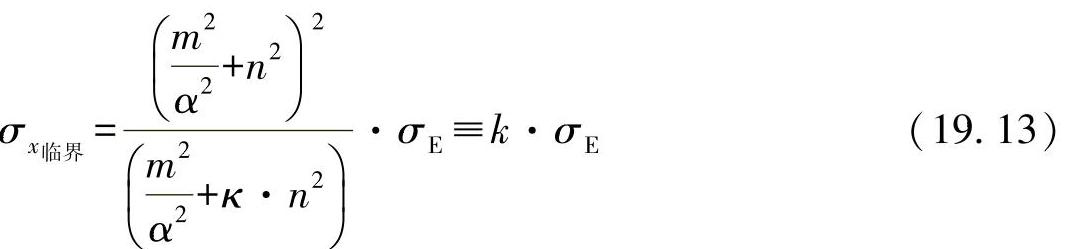
其中，k为欧拉应力的倍数。σx的最小值为所求的临界凸起应力，对于一定的半波数，由该值可导出凸起值的最小值。凸起值通常采用列表的方式给出。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
