轻量化设计：受弯梁倾斜计算与结构描述

前面已经说过，倾斜发生在高的细长受弯梁上，与弯曲扭转压弯有关。下面将研究在双对称型材上的倾斜。如图18-10中所示的示例，为一个单一载荷作用下的受弯梁。在小的力F作用下，只出现下弯。随着力的增加，受弯梁从临界力处开始发生偏移，弯曲线发生空中弯曲。由此会出现一个附加的侧面位移v，并与另一个横截面旋转ϕ相关。

首先，型材受分力F_y作用产生侧面偏移。为此有如下关系：

M_y·sinϕ≈M_y·ϕ=-E·J_z·v″ （18.41）

在分力F_z的作用下，型材发生扭转产生力矩M_t。为此有关系：

M_t=F_z·e=F_z（v-x·v′）=E·C_w·ϕ‴-G·J_t·ϕ′ （18.42）

由方程右侧可见，在型材变形中，主要是扭转阻力与拱形阻力[见方程式（10.39）与方程式（18.40）]在起作用。现在对方程式（18.42）再一次进行差分，则可得出：

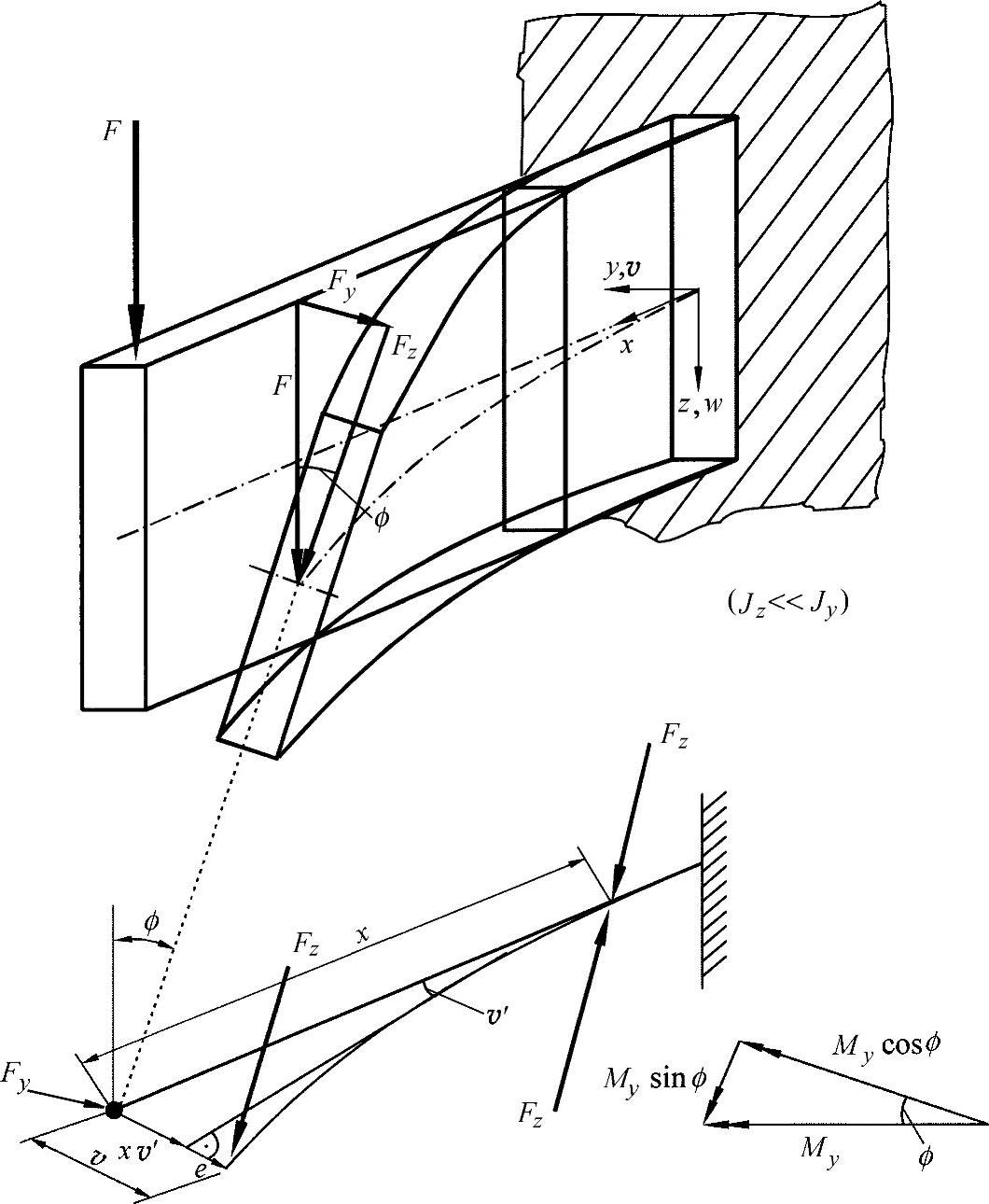
图18-10 单一载荷作用下受弯梁的倾斜（J_z<<J_y）

F_z·v′-F_z·x·v″=E·C_w·ϕ″″-G·J_t·ϕ″ （18.43）

在小变形条件下，第一项通常可以忽略不计，则有方程：

M_y·v″+E·C_w·ϕ″″-G·J_t·ϕ″=0 （18.44）

采用上式与方程式（18.41）一起可以明确地描述倾斜。

如果忽略拱形问题（这对于大多数的细长的型材是可行的），则研究可加以简化。由方程式（18.44）有：(www.xing528.com)

如果将方程式（18.45）代入方程式（18.41），则最后可得出：

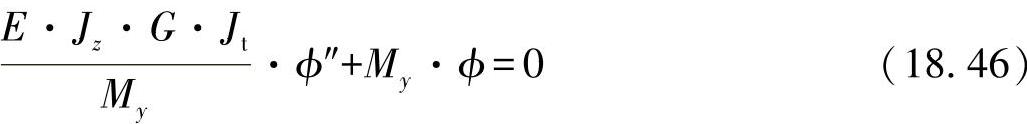
或者

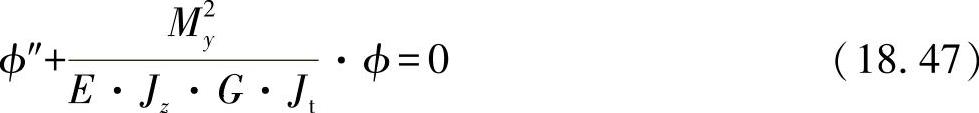
采用该方程来评估各种载荷与支座，则可得出表18-3中所示的带有针对实际情况计算公式^[4]的表格。

表18-3 无阻碍横截面扭曲下带有任意横截面桁梁的临界倾斜载荷[CZE 69]

[1]DIN 18800—1，钢构造，测量与设计；DIN 18800—2，钢构造-稳定性情形，杆与杆结构的压弯。

[2]对于圆形横截面C_W=0；对于矩形管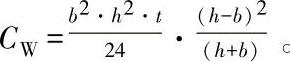

[3]a·x²+b·x+c=0，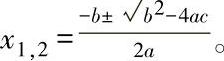

[4]在该表中，将结构作为梁加以考虑，采用的是板状结构处理，因此通过采用E/（1-v²）来代替E加以修正。