纯弯曲压弯只在理想情况下出现,即杆是准确平直的、横截面封闭以及力正好作用在中性轴上。在小变形前提条件下,这样一根杆的比例关系如图18-3所示。

图18-3 不变形杆与变形杆上力的比例关系(px=自重)
假设外力方向不变,则可将力分解为
N=F·cosϕ (18.1)
Q=-F·sinϕ (18.2)
其中,负号来自于示意图中坐标系的定向。
由于进一步的小变形与小角度变化相关,则近似有:
N≈F (18.3)
Q=-F·sinϕ≈-F·ϕ (18.4)
另外,围绕标记出的旋转中心的弯曲力矩为
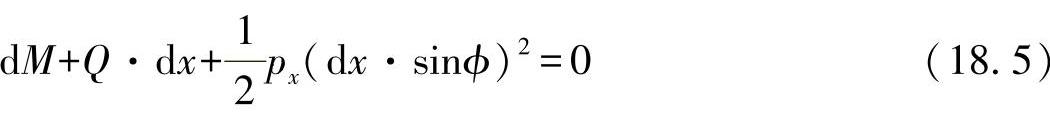
其中,px的第二项的第二阶很小,因此可以忽略不计,所以有:
M′=-Q=F·ϕ=F·w′=0 (18.6)
进一步微分有:
M″=F·w″≡-E·J·w″″=0 (18.7)
转换后可求得弯曲压弯的微分方程:

对于此微分方程采用以下方程:
w(x)=C1+C2·x+C3·cosμ·x+C4·sinμ·x (18.9)
与

可得出一个求解方程式。对方程式(18.8)两次求积分同样可求弯曲压弯,即有:
w″+μ2·w=C5+C6·x (18.11)
这里新出现的常数C5、C6通常消失在特殊的边界条件下,所以也可由欧拉方程得出:
w″+μ2·w=0 (18.12)(https://www.xing528.com)
与此匹配的求解方程式为
w(x)=C1·cosμ·x+C2·sinμ·x (18.13)
对于每种压弯情形,都有在考虑到特殊的边界条件下求解产生的方程组。
图18-4所示为典型的压弯情形,即在轴向载荷作用下的一个杆,一个支座为铰节,一个支座为导向。这里用这个例子来讨论出现的特征值问题及其评估。
由现有的方程式(18.13)出发,有:
w(x)=C1·cosμ·x+C2·sinμ·x
边界条件为
w(0)=0与w(L)=0 (18.14)
由边界条件w(0)=0,即可得出C1=0,而由边界条件w(L)=0,可得出方程式:
C2·sinμ·L=0 (18.15)
很明显,须有常数C2≠0,否则,就得出普通的解w(x)=0。这样还须考虑特征值问题:
sinμ·L=0 (18.16)
显然以上方程只能通过下式得到满足:
μn·L=n·π,有全序列n=1、2、3、… (18.17)
由此有解:
w(x)=C2·sinμn·x (18.18)
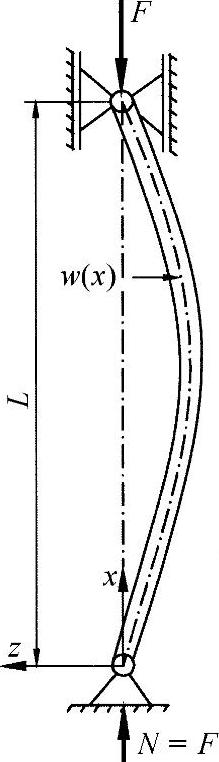
图18-4 带有确定边界条件的欧拉压弯情形(弯曲长度LK=L)
这可作为特征值问题的表征,只有这样,才可以将不确定的残余振幅确定下来。代入n=1、2、…,则实际出现的特征值(弯曲形状)可如下计算:

或者,广义计算为

对于n=1的欧拉压弯情形的全面评估如表18-1所示。这里最小值F临界总是在最小面积惯性矩Jy或Jz下得到的。
表18-1 各种边界条件下闭口横截面杆的弯曲压弯临界载荷[HOL 71]

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




