对于蜂窝形芯,可以假设,由于存在关系tW<<hK,壁的抗弯刚度与剪切刚度相比,可以忽略不计。在计算剪切变形时,从总位移中只能得出与载荷方向平行的分量。由蜂窝的构造可知,由于存在正交各向异性,据此可确定在两个方向上的剪切刚度。
情形1:轴向上蜂窝条的剪切刚度SWx(图17-8)
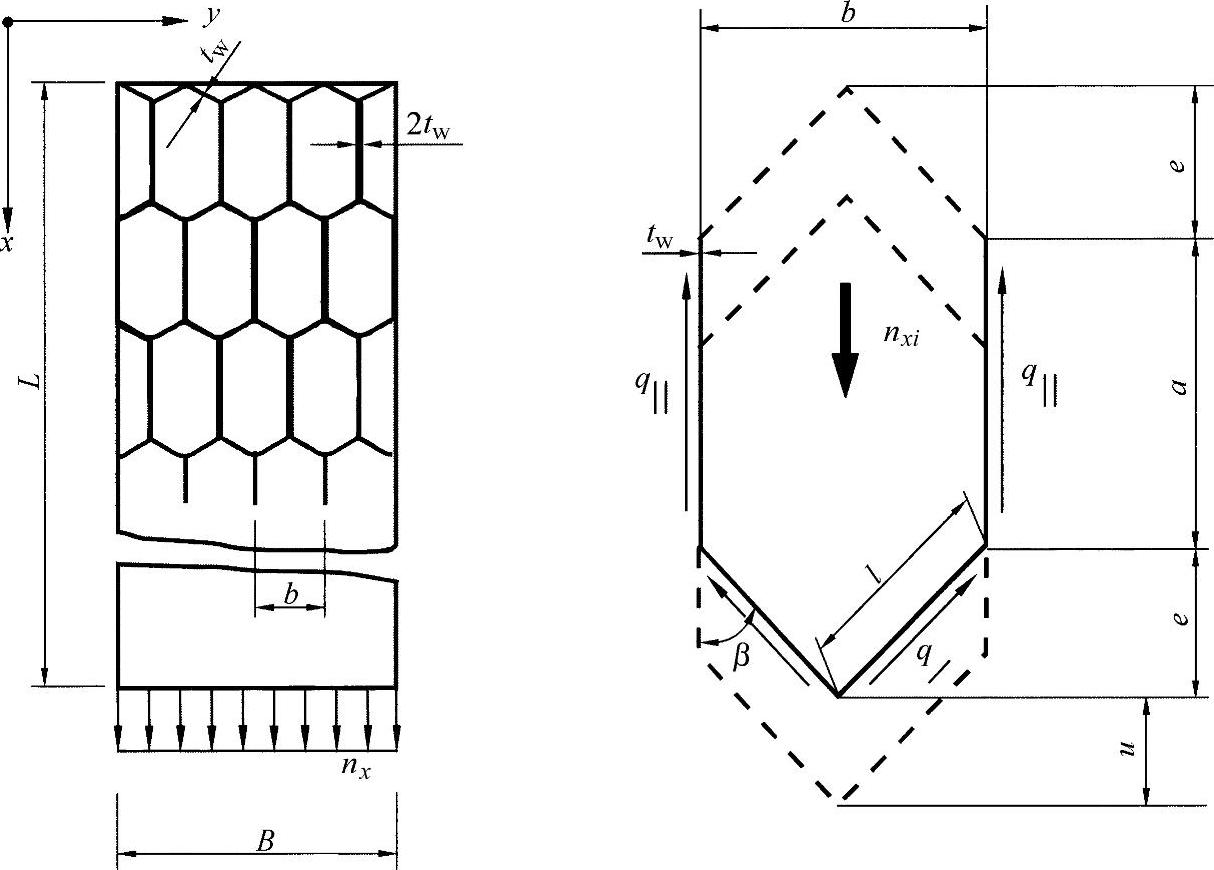
图17-8 蜂窝基本单元的轴向剪切变形
根据蜂窝形芯的构造原理,可研究一个重复的基本单元,假设其承受的作用力为nx=σx·t与nxi=nx·b。
轴向上剪切变形u的结果可计算如下:
●在平行的蜂窝壁上的切应力为
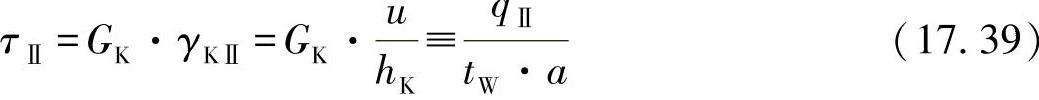
●在倾斜的蜂窝壁上的切应力为
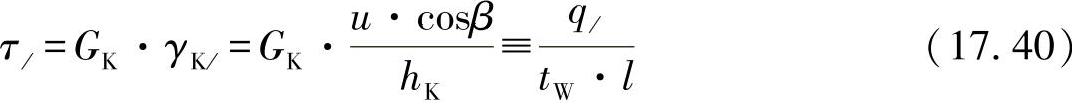
全承载的支持形芯(4个蜂窝壁)对应于外力作用的剪切力为
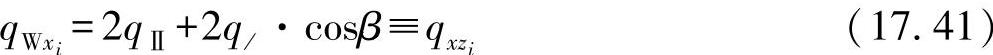
这里,由平衡条件必然得出 。
。
将方程式(17.39)与方程式(17.40)代入可得:
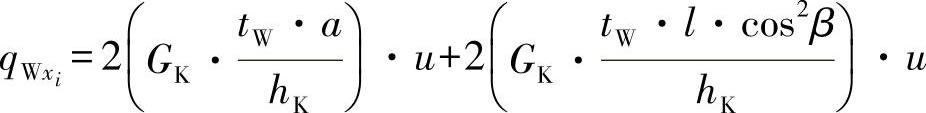
亦即引入cosβ=e/l,则可有:
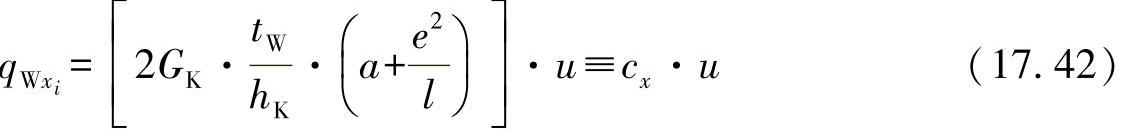
前面,在方程式(17.14)中,已经得出了轴向弹簧常数和剪切刚度之间的关系。对于蜂窝,相应地有:
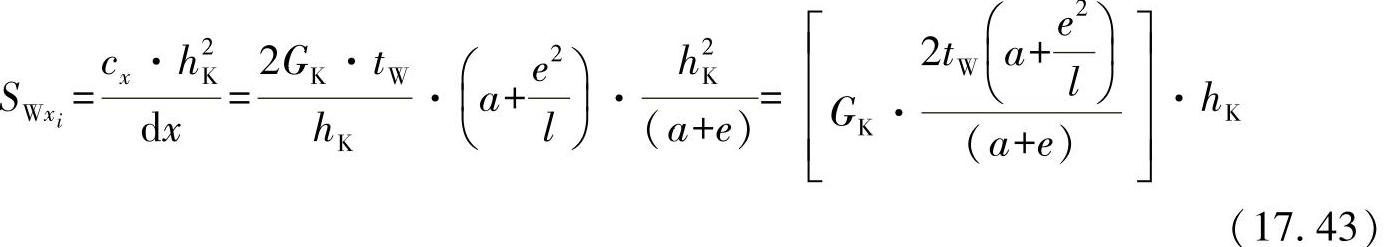
其中,蜂窝的基本长度可用dx=a+e计算。进一步地,在宽度为B的条上有i=B/b个蜂窝,所以,可得出总刚度为
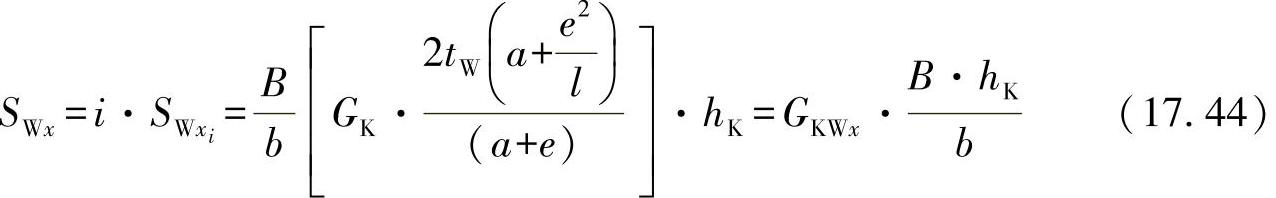
根据该方程,可用GKWx确定一个蜂窝的几何滑移模数。这样就可以定义一个基数,例如为了具有一个蜂窝形芯同样的剪切刚度,须有均质形芯。如果再有边界过渡β=0、l=e、2tW=b,则GKWx可转化为均质形芯的滑移模数GK。
现在,基于方程式(17.11),可由方程式(17.39)、式(17.40)导出蜂窝壁上产生的切应力:
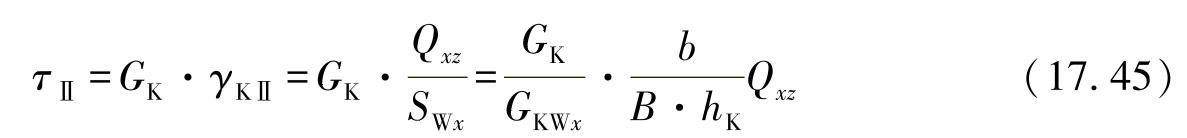
与
τ/=τⅡ·cosβ
其中,用Qxz引入在板条上产生的剪切力——内力变量。(https://www.xing528.com)
情形2:横向上蜂窝条的剪切刚度SWy(图17-9)
根据蜂窝横向的剪切变形行为,可假设:
●轴向壁对刚度几乎没有影响,因此,有τ⊥=0与γK⊥=0。
●横向壁承担所有的阻力。
对横向壁中的应力有:
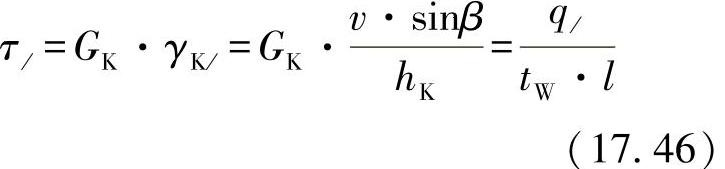
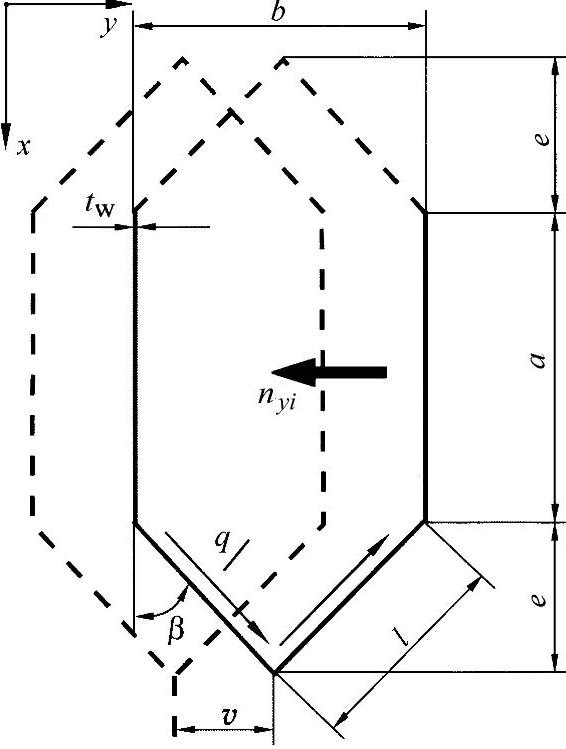
图17-9 蜂窝基本单元的横向剪切变形
传递的剪力为
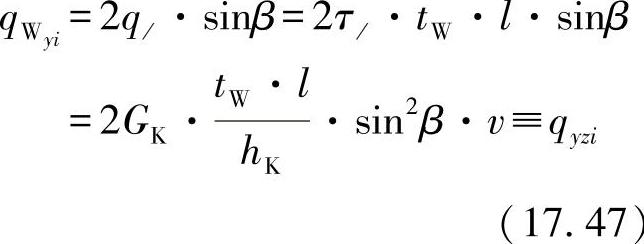
再次代入sinβ=b/2l,可得出:
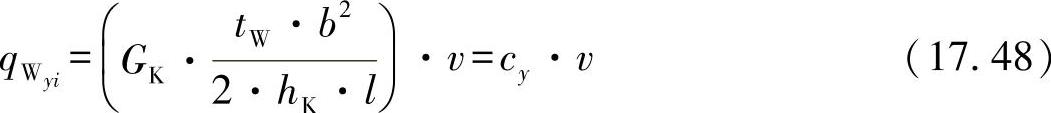
又可得剪切刚度为
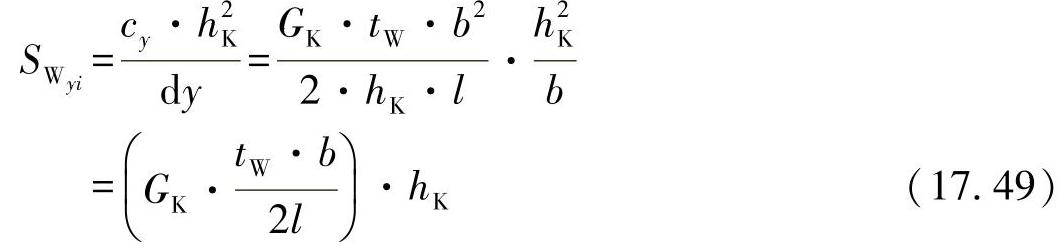
其中,dy=b。
研究一个有j=L/(a+e)个支承形芯的条,可确定出相应的总剪切刚度为
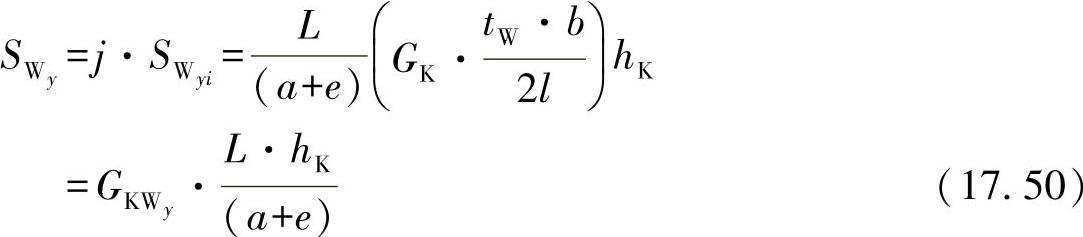
这样就可以定义一个蜂窝GKWy的几何刚度。
同样的,由边界过渡β=90°、a=0、2l=b与e=tW又可以得出GKWy=GK。由方程式(17.46)类推,则可得出蜂窝壁中的切应力为
τⅡ=0
与 (17.51)
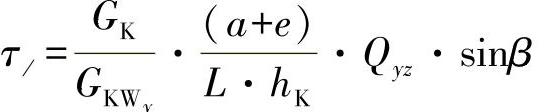
与均质形芯一样,蜂窝形芯也必须考虑到粘接缝应力问题。利用前面的关系,可计算出蜂窝边缘上的切应力为
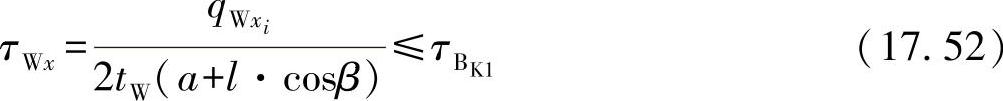
与
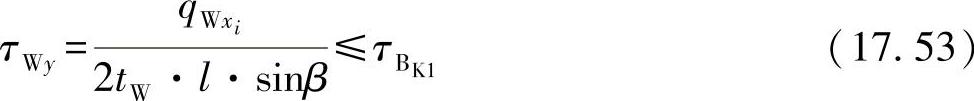
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




