轻量化设计：基本载荷情况

三明治单元最简单的构造是采用均质化形芯。对于这类单元的行为来说，需要具备以下前提条件[REI 62]：

●表层性能为线弹性的。

●表层应为水平的、平行的且薄的，以确保自身的抗弯刚度很小。

●由于弹性模量很小，形芯层不可再压缩，这样可主要承受剪切力。

从力吸收角度考虑，可将抗剪壁桁梁模型（类似于I形横截面）移植到三明治单元上来。为了更好地了解这类构件的力学性能，可以先研究在一个窄板条上的基本载荷情况。

●拉/压应力载荷：图17-3所示的三明治单元承受载荷n_x的纯拉伸力，载荷n_x大小与宽度有关。总的来说，尽管在飞机制造中也有采用压应力载荷支承或者在壳体制造中有采用平板的情形，但是在实际中很少出现图17-5所示的载荷情形。由于弹性模量不同（E_K<<E_H），构件形成了图中所示的应力应变分布。

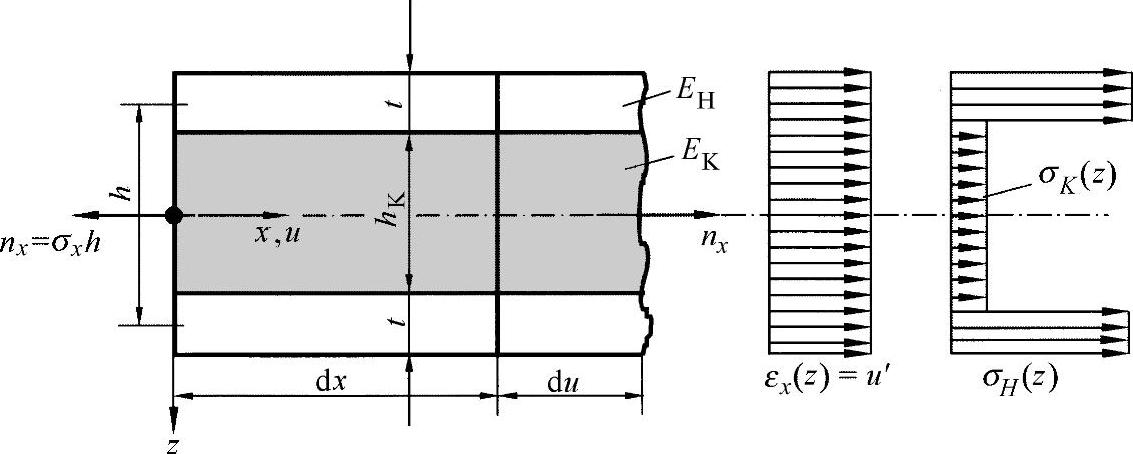
图17-3 基准宽度b=1的承受轴向应力的三明治单元

应力可如下计算：

表层的应力：σ_H=E_H·ε_x

形芯的应力：σ_K=E_K·ε_x（17.1）

其中，在可逆的应力载荷作用下，应变ε_x=常数，并且应有ε_x≤ε_B。

在x方向上，由平衡条件，可进一步有：

n_x=σ_K·h=2σ_H·t+σ_K·h_K≡D·ε_x （17.2）

这里，用D引入一个标识单元行为的塑刚度，可将其定义为

D=2E_H·t+E_K·h_K≈2E_H·t （17.3）

由于形芯的弹性模量很小，形芯的作用可以整体近似地忽略不计。

●弯曲应力载荷：图17-4所示为承受纯弯曲的三明治单元及其应力应变分布。一般来说，弯曲表明了主要的载荷情况。以宽度为标准的作用弯曲力矩计算如下：

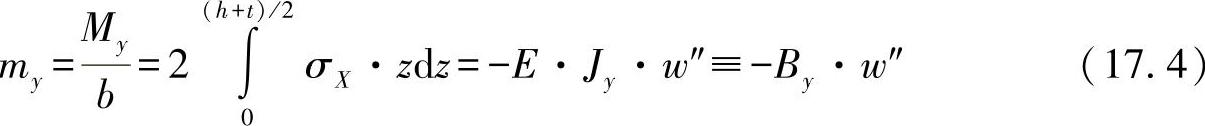
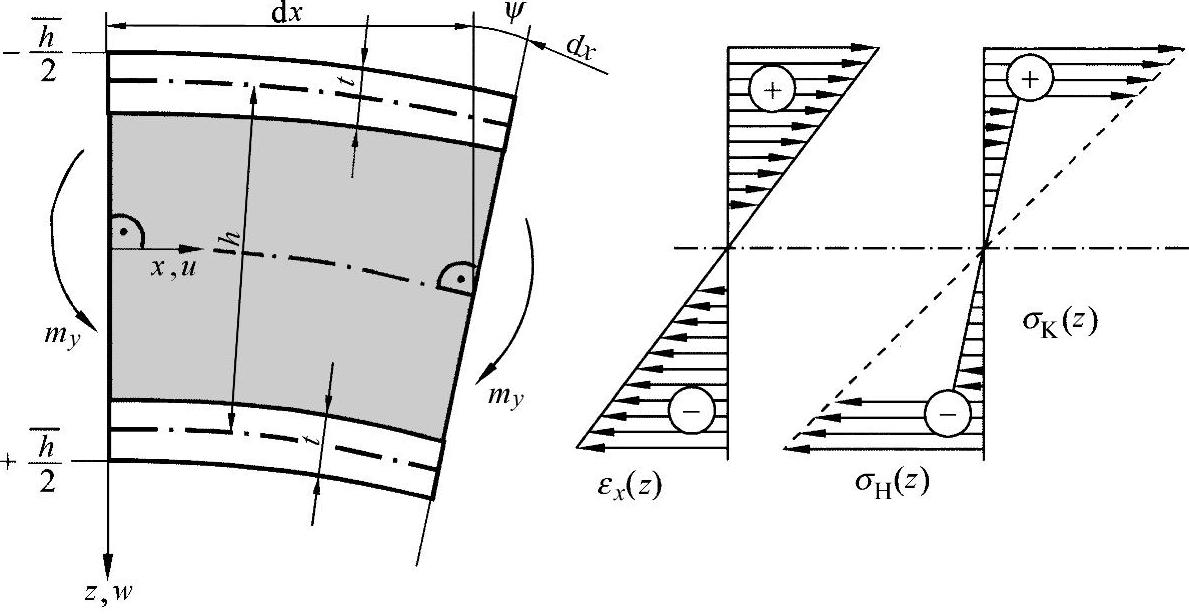
图17-4 受弯曲应力的三明治单元，基准宽度b=1

在该表达式中，也必须考虑不同的局部应力分布，即：

σ_H（z）=E_H·z·w″与σ_K（z）=E_K·z·w″ （17.5）

可得出抗弯强度为

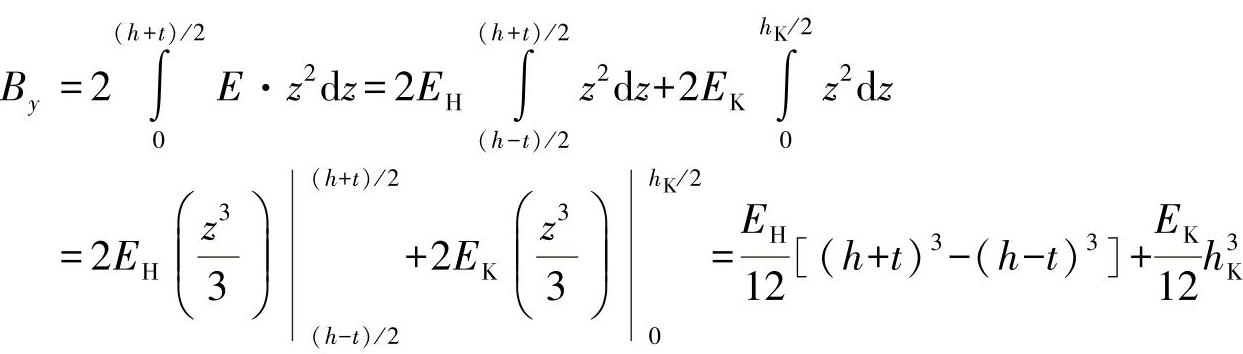
整理集合后可得出：

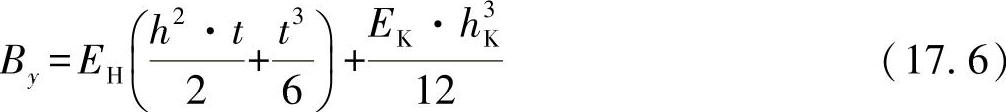
假设h≈h_K，E_K<<E_H，并忽略表层的自身抗弯刚度，则抗弯刚度可计算为

对于比例t/h<1/4，该表达式已经达到了非常好的近似结果。

●切应力载荷：作为前面情形的补充，如下面所示的剪切力弯曲下的三明治单元。考虑到单元性能，这里表层相反力偶的作用非常关键，这些力偶造成了图17-5所示的不连续的切应力载荷变化。

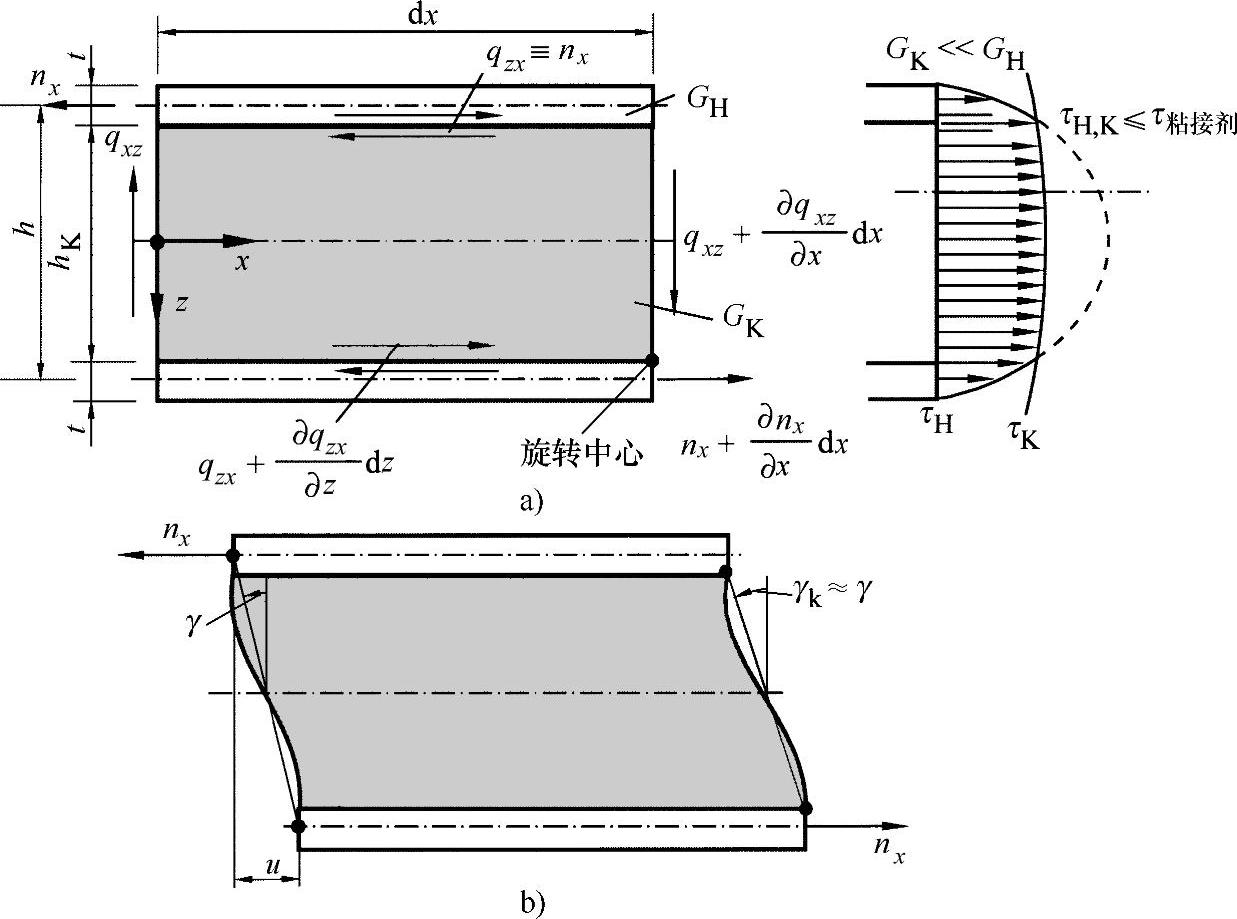
图17-5 临界剪切下的三明治单元基准宽度b=1

a）载荷与应力载荷状况 b）扭曲状况(www.xing528.com)

在产生的位移u与作用在表层的力偶n_x之间应当存在如下的比例关系（弹簧定律）：

n_x=c·u （17.8）

其中，由几何形状变形可得出：

u=h_K·γ_K （17.9）

根据在无变形的形芯单元（自由开口剪切单元）上的力矩平衡条件，可进一步得出力的内在关系为

q_zx·h_K=q_zx·dx （17.10）

其中q_zx≡n_x，则对剪切力组件可有：

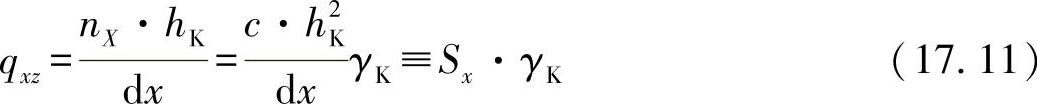
上式中，用S_x引入剪切刚度。为了进一步确定剪切刚度，须利用切应力表达式：

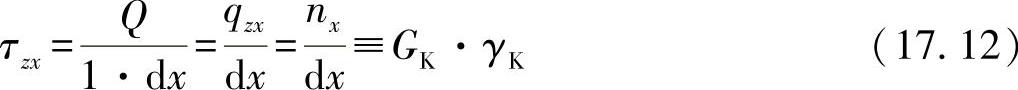
这里，再考虑方程式（17.9）并按照n_x求解，可得出：

或者对于弹簧刚度有：

将这些比例常数代入方程式（17.11），可得出：

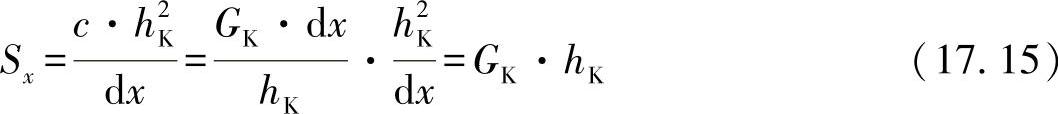
另外，还要考虑到切应力的分布。在这里，初始关系为在内部的片状形芯层的平衡条件（见8.3.3小节）：

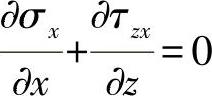
经过积分有：

其中，∂σ_x/∂x产生了一个法向应力梯度。不过，法向应力梯度以这种形式出现并不恰当。对于线弹性材料行为，由于作用的力矩与产生的应力之间的比例关系，该应力梯度可如下替代为

就是说，应力对于力矩的最终微分系数比例相同。由此亦有：

另外，还应当考虑到，力矩的导数始终等于剪切力，即：

对于方程式（17.18），最后可得出：

采用方程式（17.4）与方程式（17.5），可计算应力变化为

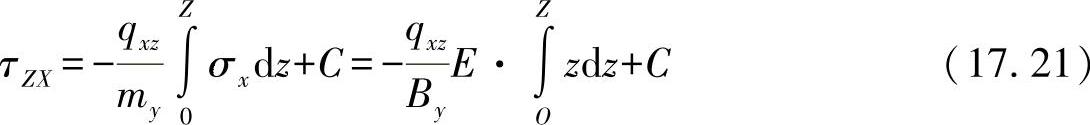
其中，外部作用的力等于内部产生的力，即q_xz≡n_x。

以上说明了带有均质形芯三明治单元的三种基本应力载荷情形。这里应当清楚的是，刚度才是最重要的特征值。