闭口框架的内力变量研究及计算方法

实际中经常碰到的一个问题是研究闭口框架的内力变量。图16-6所示的水平框架为一种可能的结构形式。

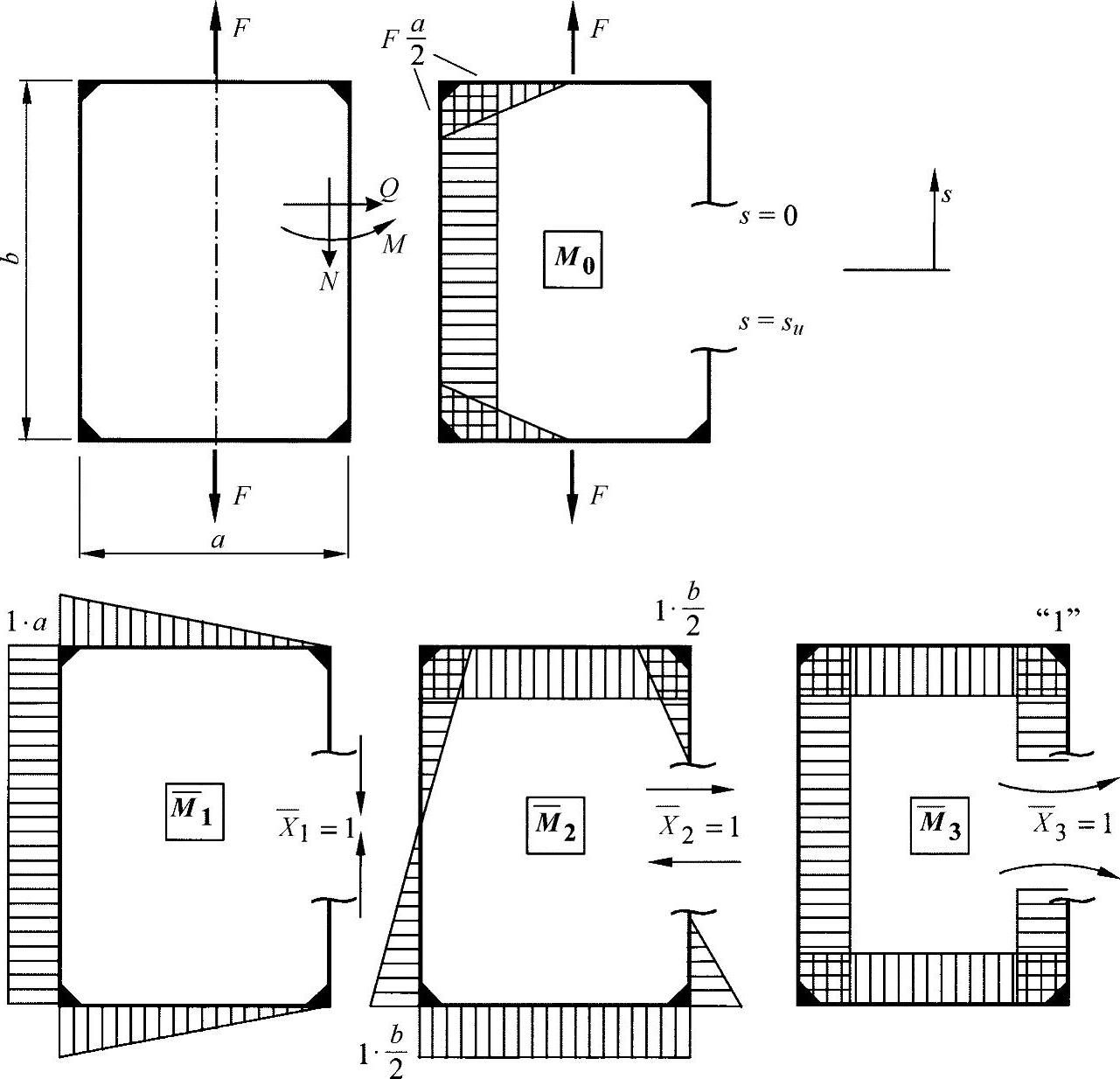
图16-6 在单一力矩应力载荷作用下空间内的内力变量变化

在框架的每个臂上，都作用有三个内力变量N、Q与M，因此框架的内部是三重不确定的。将一个纵向臂切开（这里以最适当的方式切开），则可生成一个静态确定基本系。由于在这个位置的初始结构上不能发生位移，因此可通过代入相互作用的力X_k进行回算。在忽略法向力和切向力的情况下，可用其计算弯曲力矩M的值。

通过切开一个臂，可首先生成一个基本系，并研究其中的力矩变化M_o。在这个截面位置上可能产生的变形可通过三个多余的“一”力回算：

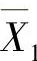=1（作为内法向力）

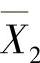=1（作为内切向力）

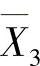=1（作为内力矩）

在实际高度中要求的静态多余的力X_k可通过方程式（16.8）的位移条件公式得出，即有：

载荷情形1：δ₁₁·X₁+δ₁₂·X₂+δ₁₃·X₃=-δ₁₀

载荷情形2：δ₂₁·X₁+δ₂₂·X₂+δ₂₃·X₃=-δ₂₀ （16.10）

载荷情形3：δ₃₁·X₁+δ₃₂·X₂+δ₃₃·X₃=-δ₃₀

这里，位移影响指数依然是未知的，现在可如下确定（参见图15-13）：

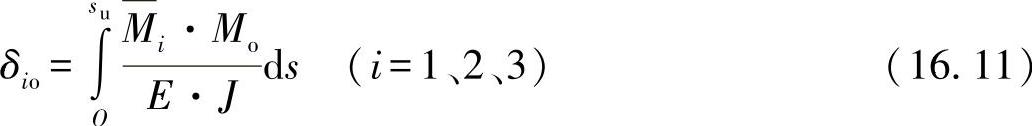
与(www.xing528.com)

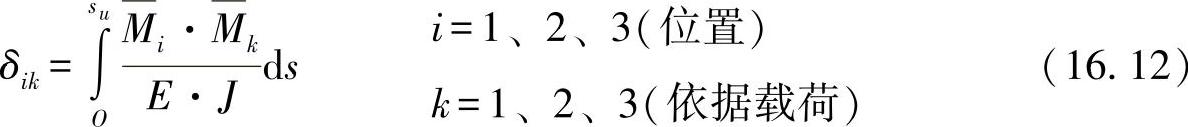
为求解方程式（16.10），可适当地利用所谓的Cramer规则^[1]。

多余的力可如下计算：

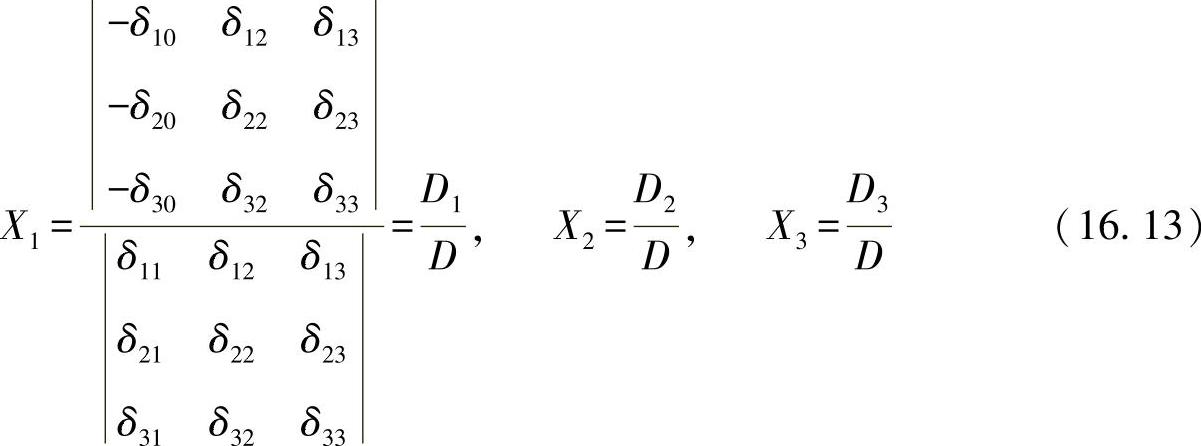
其中，D_i为计数行列式；D为恒定的分母行列式。

对于给出的框架，可以计算出在任意位置上的内应力值“弯曲力矩”为

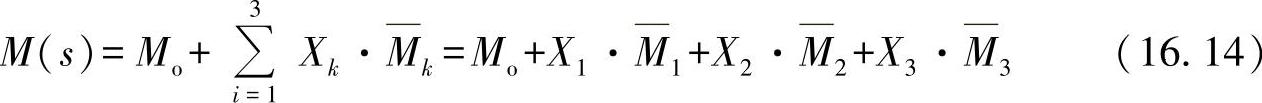
书后练习19所举的例子有助于进一步理解上面介绍的方法。

对于分析来说，法向力和切向力也很重要，因此，可以对上述表达式加以展开。在广义的情形下，可计算出位移影响指数为

与

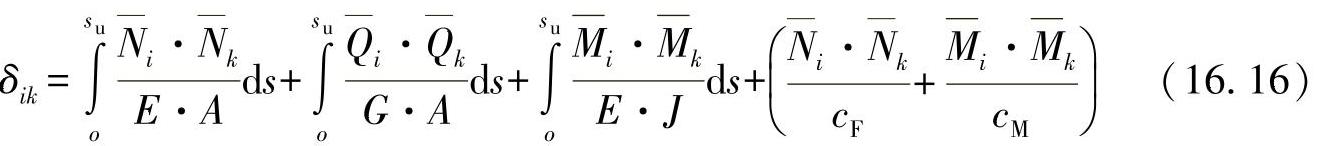
除了法向力和切向力的影响外，还可以求解出回弹的分量（C_F、C_M）。

[1]Cramer规则中，在D_i中属于未知x_i的系数δ_ji可用右边的δ_io来代替。