静态不确定结构的弹性方程在轻量化设计中的应用

对于静态不确定桁架结构或者梁结构的应力分析基于如下的基本考虑，即通过求解外在联系（略去支座自由度）或者内在联系（引入铰节，切开杆）可以生成一个静态的与运动学可确定的基本体系。这样做首先会破坏一个结构的几何尺寸。在这样一个静态确定基本体系中，所有内力变量可以被作为零力N_o、Q_o与零力矩M_o，由平衡条件加以研究。

特别重要的是位置（i）处的位移与角变化，结构在这些位置上被切开。在这里，这些特征值作用于配合间隙。因为它们是由计算的零载荷引起的，可用δ_io标识。但是，真实的结构必须是在位置（i）处连续变化的，即位移在所有的支架上消失。因此，须对间隙δ_io进行回算，在截面位置的间隙上产生了力值X_k（静态多余力）。应力载荷的变化又可以由平衡条件加以确定了，由此，也可由力X_k计算出位移δ_ik。随后可用此位移消除零系中的间隙，则又重新生成了几何一致性。

实际中，先将静态多余力作为单位载荷进行计算，然后力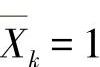作用于相应的在位置（i）处的位移为δ_ik的内力变量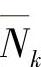、、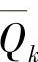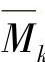。实际的位移则为X_k·δ_ik。

根据以上分析，数值n的静态多余力在位置（i）处产生的实际总位移：

如果假设在这个位置上不允许发生位移，则须有相容性条件：(www.xing528.com)

上式描述了对于静态多余力X_k的一个带有n个方程的方程组，如下例所示，对该方程组可以加以清晰地计算。

实际的内力变量：

可用由静态多余力得出的内力变量，由作用的零力叠加得出。