【摘要】:如果由R封闭的框架存在一个框架桁梁结构,则按照[SZA 84],内在不确定性度为Ua=3R 图16-3中补充显示了一个带有铰节的框架结构。不过,这里存在特殊情形,就是不需要考虑铰节,因为如前所述,该结构中没有柔性分系相连接。从这个意义上来说,只有框架通过杆与刚性角连接在一起的时候,才必须要考虑到铰节。
在一个外在静态确定的支座框架的内部,力的变化只有在如下条件下可由平衡条件加以确定,即框架不是单次封闭或者多次封闭的。因此,按照图16-2所示即可给出支座力。如果将框架在任意一个位置上切开,则三个相互不依赖的内力(No、Qo、Mo)就自由了。
由于带有支座反作用的外力已经处于平衡状态中了,因此再没有可用于研究内力变量的静态条件了。图中所示的框架内部是三重静态不确定的。
如果由R封闭的框架存在一个框架桁梁结构,则按照[SZA 84],内在不确定性度为
Ua=3R (16.3)
图16-3中补充显示了一个带有铰节的框架结构。不过,这里存在特殊情形,就是不需要考虑铰节,因为如前所述,该结构中没有柔性分系相连接。从这个意义上来说,只有框架通过杆与刚性角连接在一起的时候,才必须要考虑到铰节。尽管有9个不能马上确定的反作用力,依然可以确定,框架支承结构是外在静态确定的。
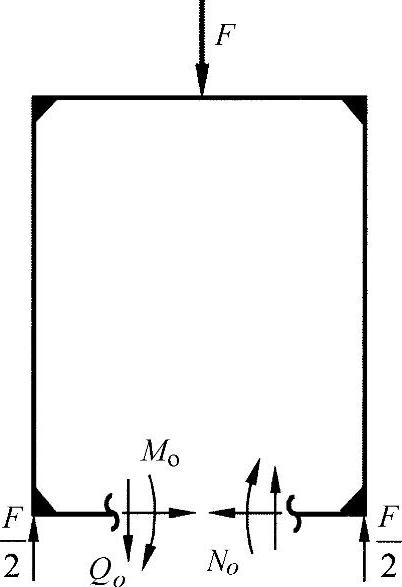
图16-2 具有刚性角的框架内的未知量(https://www.xing528.com)
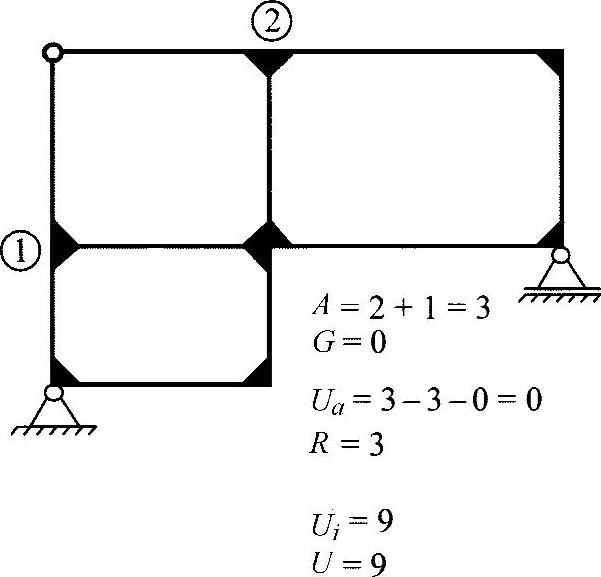
图16-3 带有铰节的框架结构的计算条件
至此,可确定一个组合式框架桁梁结构(图16-3)的总的静态不确定性度为
U=Ua+Ui=A-3-G+3R (16.4)
这里,度U与一个结构的所有未知量的数量是一致的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




