做功原理与轻量化设计

通过能量公式只能得出在力作用位置上沿着作用力方向上的位移。能量表达式更重要的意义在于[CZE 67]，通过概括可以在任意位置上确定位移。下面通过在两个支座上的横梁为例（图15-2）来进一步说明做功原理。

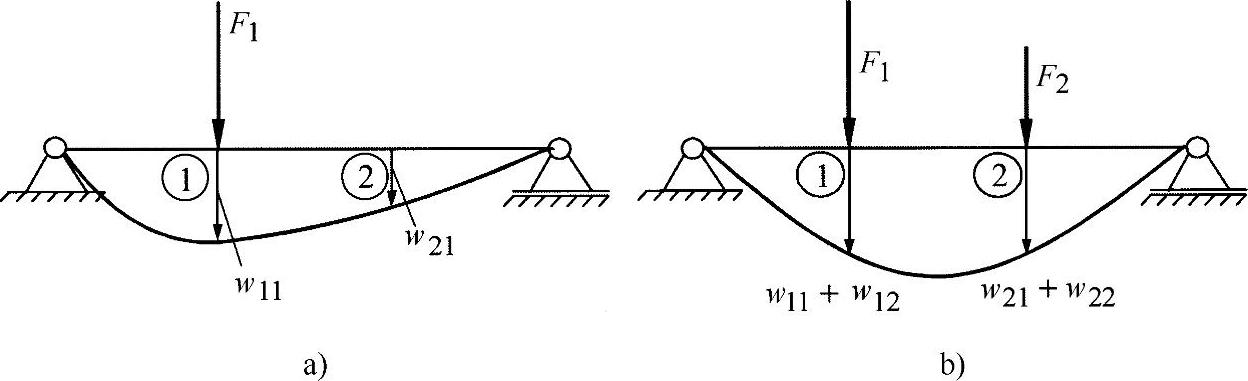
图15-2 梁的挠曲

a）单一力F₁作用 b）载荷F₁与F₂作用

首先，横梁只受力F₁载荷。在力作用点①发生了位移w₁₁。在任意位置②可确定位移w₂₁。如果假定在力与位移之间存在一个线性关系，则有：

w₁₁=F₁·δ₁₁

与 （15.6）

w₂₁=F₁·δ21

这里用δ_ik（i=位置，k=成因）引入位移值或者挠性值。

由力与位移可得出按比例分配的功：

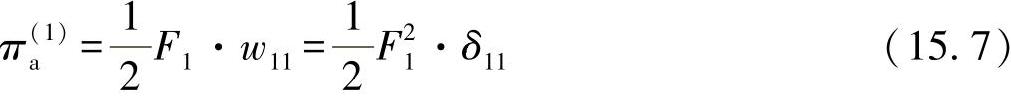
如在已经承受载荷的桁梁的位置②处施加另外一个力F₂，则会出现附加的做功分量，即有：

●带有自身位移的力F₂的功：

●附加的功：

π_a^（3）=F₁·w₁₂=F₁·F₂·δ₁₂ （15.9）

通过力F₁产生的位移w₁₂，是由力F₂在位置①引起的。这里没有预因子1/2，因为在位移w₁₂开始时F₁就已经达到最大值了。

由此，梁的总功为

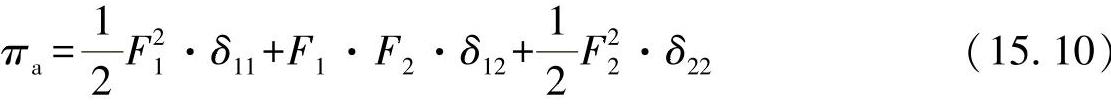
按照“Betti定理”，功的大小与力的顺序无关。

如进一步用力矩线将导致力矩变化的力分开，则有：

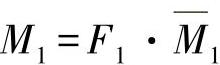
与 （15.11）

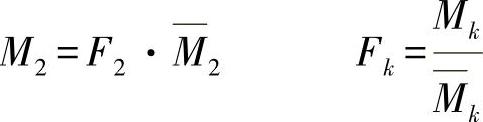
与方程式（15.6）等效，力矩M_i描述了针对力F_i=1的力矩线。

为了重新确定变形，可由能量平衡公式π_a=π_i出发。对以上表达式进行相应地计算，可得出：(www.xing528.com)

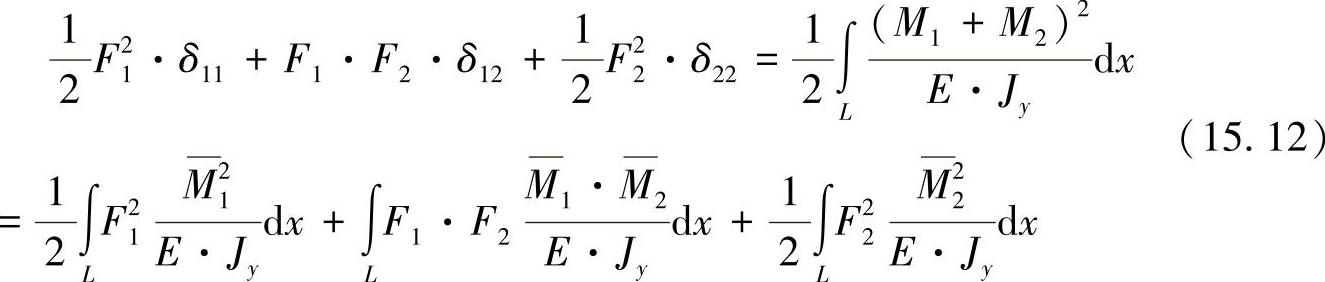
由于计算一般是以小位移作为前提条件，载荷导入的顺序并不重要。因此，也可以对力矩运用叠加原理。如果对方程式（15.12）中的右边与左边进行对比，可以看出广义的关系为

根据w_ik=F_k·δ_ik与方程式（15.11）可得出：

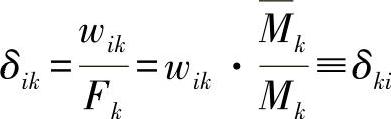（Mawxell定理/可逆定理）

以及

由做功原理导出的规则如下：

如果一个桁梁在位置k受载，而要研究位置i处的位移，则可以在位置i处，在所研究的位移方向上引入一个虚拟力值“1”：根据虚拟力值来确定实际的力矩作用过程M_k和力矩变化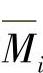，由乘积的积分可得出要计算的位移w_ik。

在应用这一关系时必须要注意，功是由力的值乘以位移得出的。因此，存在如下关系：

力×位移

弯曲力矩×角

扭转力矩×转角

在实际应用中已经证明了，方程式（15.14）的积分可用于求解最重要的载荷情形。图15-3列出了一些常用的数值，它们出现在两个力矩线的乘法以及最后的积分中。在方程中用数值因子c乘在前面，可得到要求的值w_ik：

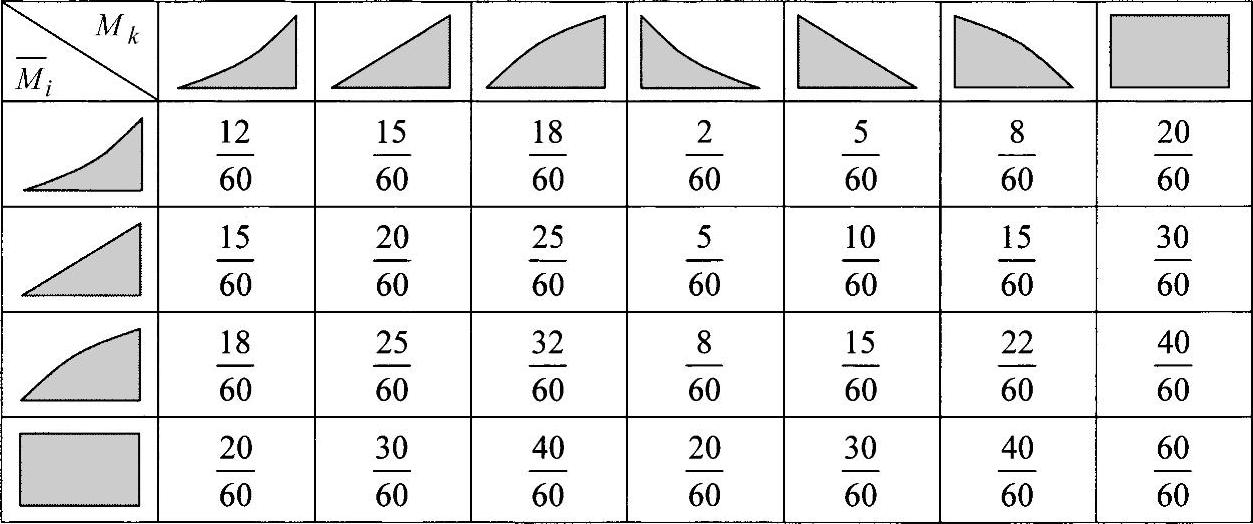
图15-3 数值因子c的表格

这里，M_i和M_k为力矩面积相应的边界值，L为桁梁的长度，E·J为假设的抗弯刚度。

图15-4简短示例了上表在悬臂桁梁上的应用。

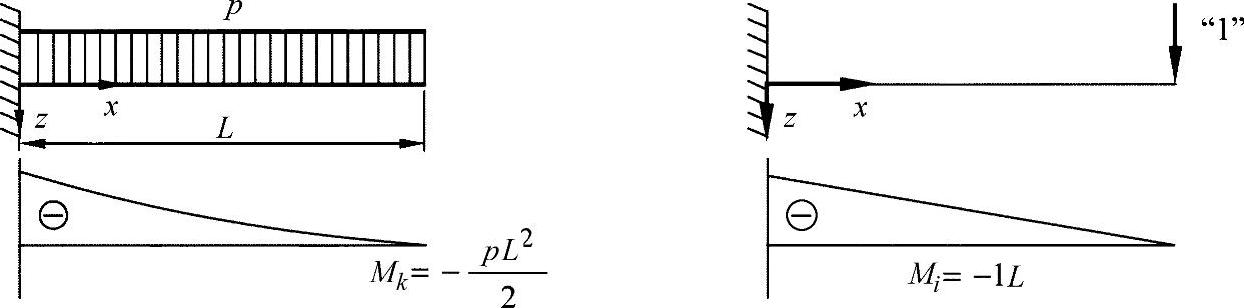
图15-4 分布载荷作用下的悬臂桁梁

根据方程式（15.15），可得出承受载荷的情形下最终的挠曲为

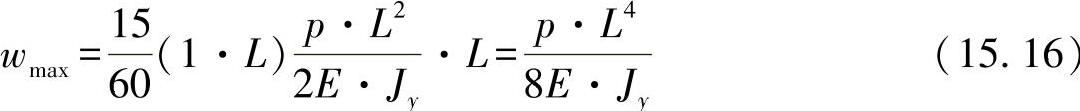
其中，预因子c=15/60可从表中找到。相应地，可确定每个中间位置w（x）。

以上说明了一个简单方法，即如何确定任意结构的挠曲。