开口结构中剪切力流的计算

实际中可以经常看到，由于功能上的需要，箱形型梁上往往有开口[DER 82]。这种结构形式用于窗户、门或者行走机构开关等。由于开口的存在，型材变得薄弱了（更小的抗扭强度），一方面导致更高的扭曲，另一方面也导致应力载荷重新分配。图14-3所示为在一个单元格内的开口，这里采取简化的方式，即整个缺了一个板壁。这类典型的情况在飞机机身或者机翼上可以看到，行走机构轮毂必须在这样的开口里进入或者放出。

图14-3 带有临界开口的箱形梁

在开口结构中，依然假设由外力矩（M_x=常数）引起的扭转作为载荷，同时还假定，载荷也作用于开口区域。另外还需要假设，在力流变化过程中出现的干扰局限于开口区域与两个相邻接的单元格中。此例中，主要研究应力载荷变化的情况以及如何消除干扰。

图14-4所示为在假设的模型中实际产生的剪切力流分布，从这一点来说，就是从开口箱体转换到闭口箱体。

在接合区域的干扰和在相邻单元格的去除量可由平衡条件导出。对于开口箱体有：

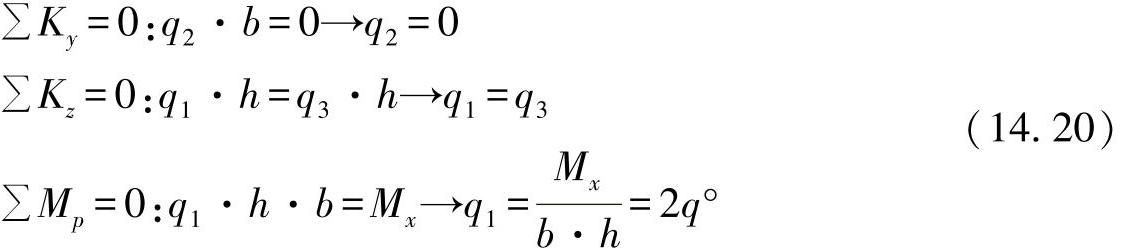
就是说，在相对放置的盖板开口上没有出现剪切力流，而侧壁上剪切力流的大小则是外基准剪切力流的两倍；因此，由于平衡反应，弦杆上的法向力产生了剪切力流q₁与q₃，它们可以由杆平衡条件确定如下：

2N+q₁·L=0

图14-4 在导入的M_x作用下箱形梁中载荷变化

a）分割的开口箱体 b）分割的闭口箱体

另外，也可以根据平衡条件来研究相邻区域。这里假设为，前置单元格与后置单元格将干扰完全消除。可得流为

∑K_y=0：q₂·b=q₄·b→q₂=q₄ （14.22）

∑K_z=0：q₁·h=q₃·h→q₁=q₃ （14.23）(www.xing528.com)

只有这三个方程还无法确定四个未知的流。通过杆上的平衡条件，还可以得出另外一个方程式：

q₁·L-q₂·L+N=0

q₁-q₂=q° （14.25）

这里，用方程式（14.21）代替N。

根据以上的四个方程式（14.22）、（14.23）、（14.24）与（14.25），通过简单的消除，可得出未知的剪切力流：

与

最后，简要总结如下（图14-5）：

●在开口区域，剪切力流大小增长为无干扰区域基准剪切力流大小的两倍。

●在底板（开口）区域，剪切力流减小为零。因此，侧壁承受的载荷特别大，在应用时必须给予加强，采用合适质量的材料，因为这里适用关系：

图14-5 在开口箱体上剪切力流的分布（图中画出的是结构对称的一半）