轻量化设计：扭转应力载荷计算基础与构件结构

采用四弦杆模型时，需要优先解决的问题是计算箱型桁梁内力的导入，这些力是由在任意位置上导入的扭转力矩（M_xi=M_x=常数）引起的。采用这一解法须假设，最后的隔板与刚度很高的结构连接在一起，可近似为一个固定支座。图14-2说明了这一情况。实际中感兴趣的是如何抵消载荷。

首先，一个单元格的内在应力载荷状态必须等效于作用扭转力矩。由扩展的平衡条件可以得出，除了剪切力流，在弦杆内还存在着法向力。根据前面的求导结果即可计算出剪切力流：

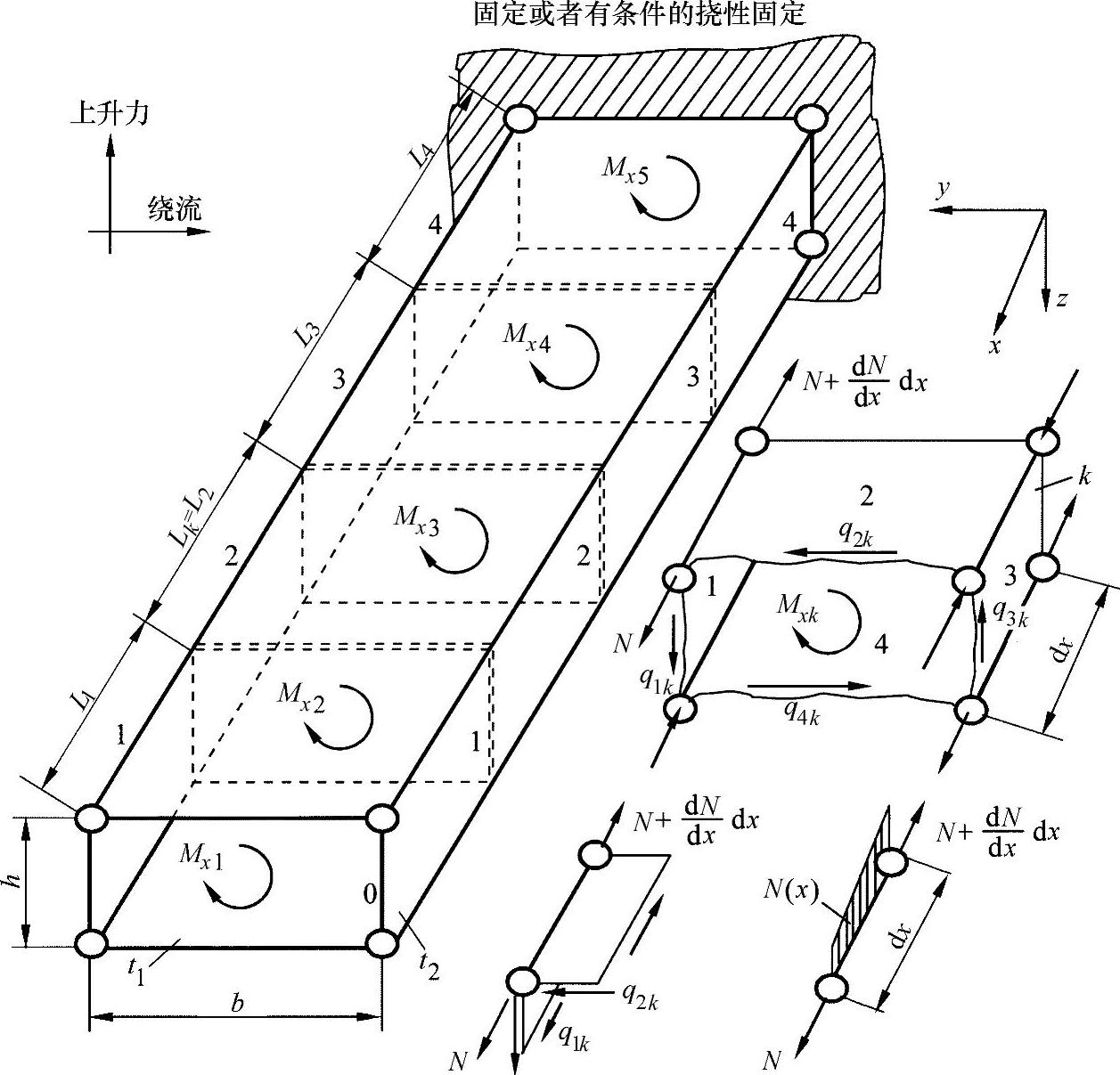
图14-2 带有隔板的箱型桁梁（机翼模型）的载荷模型

q_1k=q_3k=常数，q_2k=q_4k=常数，但是q_1k≠q_2k （14.4）

对于一个断面的横截面平面上的旋转中心来说，有：

q_1k·h·b+q_2k·b·h=M_xk （14.5）

从在一个弦杆上的平衡条件出发，可得出：

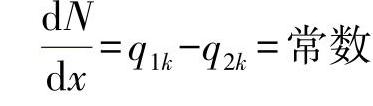
这里，在每个单元格中，法向力的线性变化都是封闭的：

借助以上关系，可得出对于流q_ik的方程组。在该方程组中，N_k依然是不确定的。为了确定N_k，可适当地应用变形功最小值的表达式。首先进行适当转换，然后采用方程式（14.5）消去q_2k，将其代入方程式（14.6），则可有：

现在，导入的M_xk应当引起了一个基准剪切力流该剪切力流可以按照类均匀横截面加以计算（第一布莱特公式）：

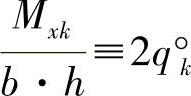
对于每个单元格，可以简单地确定基准剪切力流值q°_k。据此，上面的方程式也可写成：

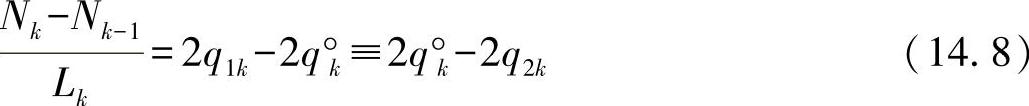
对后面求解剪切力流的逆算法，须先求解方程式（14.8）：

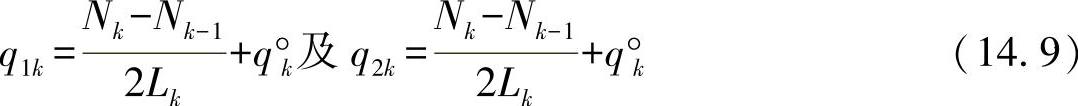
现在，进一步对法向力逐段的线性变化进行展开：

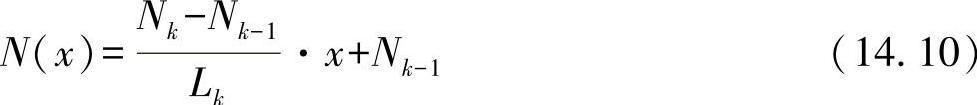
则可以确定对于一个k场的变形能，有：

●对于在四个弦杆上的法向力：

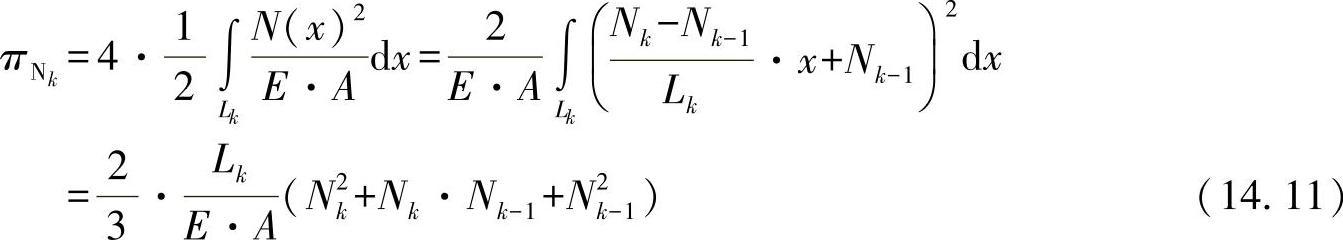(www.xing528.com)

●对于在两个盖板上的剪切力

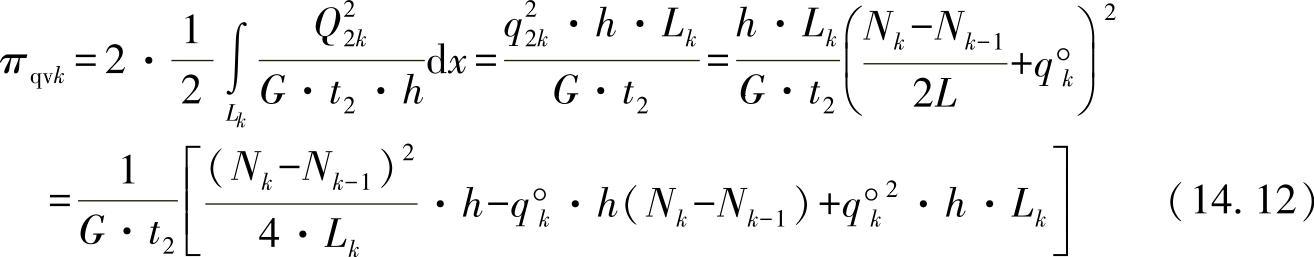
●对于在两个侧板上的剪切力

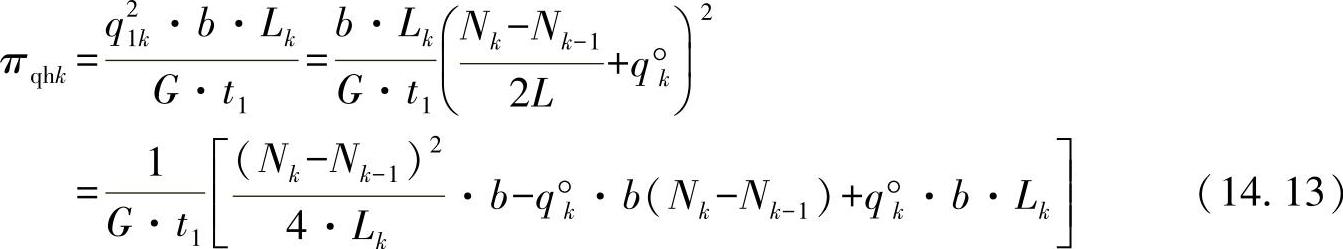
对于一个单元格（这里为左单元格）的总变形功为

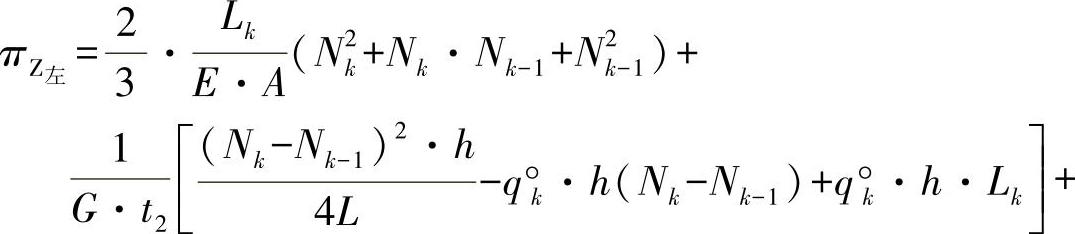
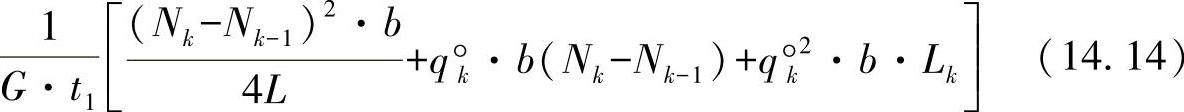
通过指数的指数，也可以给出一个右单元格的变形功。现在，将两个部分功相加，并相应求导（卡式定理），则可得出力的耦合方程：

这里，考虑到常数A、L_k和t_i，可以求得相应的导数为

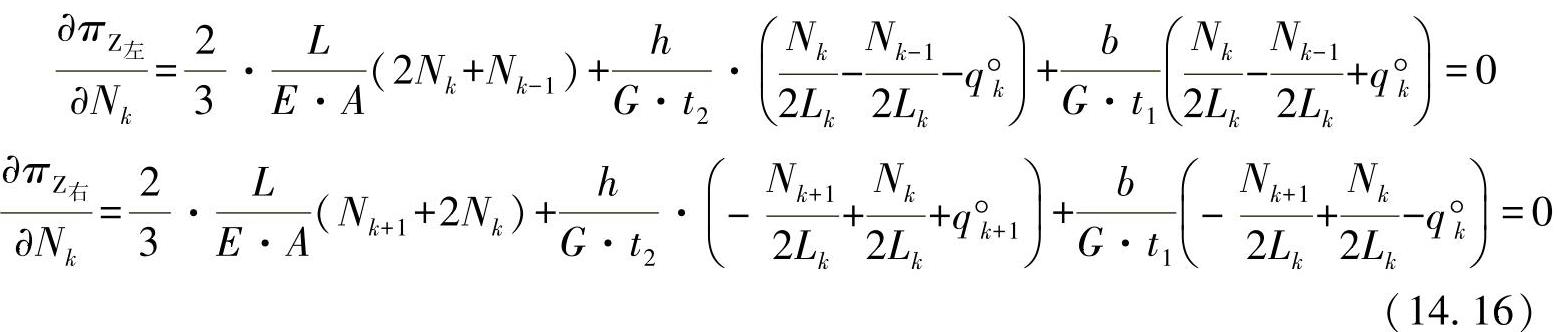
整理后，可得到方程：

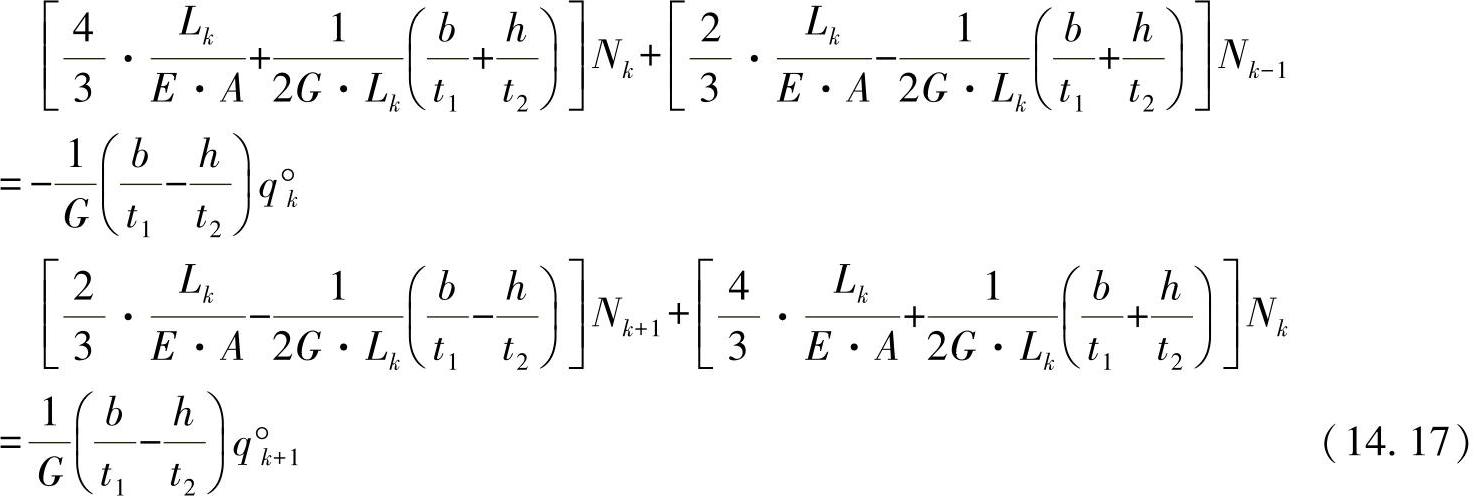
加上叠加的方程组：

α₀·N_k+1+2α₀₀·N_k+α₀·N_k-1=β·（q°_k+1-q°_k） （14.18）

这里，系数α₀、α₀₀、β由前面的方程来分配。

现举例如下。对于一个三单元格的构造，求解方程式（14.18）。为此，须展开下面的方程：

对于k=1，α₀₁·N₂+2α₀₀₁·N₁+0=β·（q°₁-q°₂）

对于k=2，α₀₂·N₃+2α₀₀₂·N₂+α₀₂·N₁=β·（q°₂-q°₃）

对于k=3，0+2α₀₀₃·N₃+α₀₃·N₂=β·q°₃

最后一个单元格应该通向固体墙壁，对此，总是可以采用方程式（14.19）进行计算。所以，最后的方程为

2α₀₀·N_k+α₀·N_k-1=β·q°_k （14.19）

在上面的方程中，q°_k消失在固体的终端墙壁里。借助法向力N_k可以确定q_ik。