前面假设,板在切应力载荷作用下不发生弯曲。但是,也存在另外的可能性,即切应力载荷一直增加到超过临界凸起应力τxz>τB临界。临界可理解为极限应力,在临界状态下,初始平直的板材达到了一个新的平衡状态(稳定极限),该状态与力的重新分布相关。达到新平衡状态的结果是在板上产生了一个特殊的应力状态,可将其标识为理想拉伸场。为了解释这一现象,可以首先研究一个薄盘。当应力σx、σz与τxz作用在一个薄矩形盘的边缘上时,已知其主应力(图13-2)作为最大应力,则可如下计算:

传递到剪切板上(这里的基本假设为:σx=0,σz=0,τxz=τ)的主应力为
σ1=+τ(拉),σ2=-τ(压) (13.4)
假如板材上的凸起应力超出极限值,则板材会由于承受压应力载荷而产生皱褶。这样一来,应力会重新分配。对于切应力的增加,拉应力σ1(在皱褶方向)增长的速度要高于压应力σ2(垂直于皱褶方向)增长的速度。在极限情况下可以得出,这种情形容易产生弯曲的板材。而通过皱褶处恒定的凹陷,可抵消垂直于皱褶方向上的所有吸收的能量。对于理想拉伸场,可设定σ2=0。
在这样的作用关系下,有必要确定板材上的主应力σ1最后与外载荷τ(q)的关系。为了解释这一点,取图13-3中的板材主应力方向上的截面进行研究。

图13-2 理想拉伸场的主应力方向

图13-3 理想剪场的主截面方向
根据左截面单元的平衡条件,有:
∑Kx=0:(σ1·A)cosα-τ(A·sinα)-σx(A·cosα)=0 (13.5)
由于在这一个方程式里有两个未知数,因此还需要另外一个方程式才能求解。该方程式可由右面的截面单元导出:
∑Kx=0:σx(A·sinα)=τ(A·cosα) (13.6)
将式(13.5)乘以sinα[1],代入式(13.6),有:
σ1≡|σ2|·A·sinα·cosα=τ·A·sin2α+τ·A·cos2α≡τ·A
亦即,应力与板场承载能力[2]的关系为:

至此,皱褶角α的大小依然未知。现在,该角的大小应在一任意中心剪场上按照卡式最小功定理公式来加以确定。
图13-4中显示出了皱褶的应力载荷极限状态。经过前面的推导已经得出,通过其他场的叠加,在板材上还存在有法向力流nx、nz,由此可得出围绕框架的支柱与弦杆的应力载荷状况如下:
●支柱中力的大小可由邻接的剪场求出:


图13-4 剪场中力的作用方向,在这里,场全部是连通的
这里,通过考察截面单元可得出:
nz=q·tanα
●弦杆中力的大小可通过一个剪场确定为:
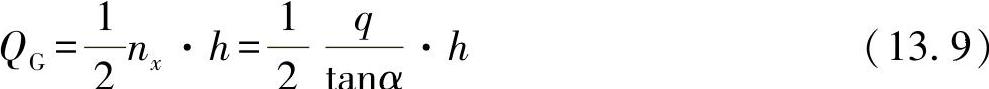
在这里,也可以通过考察截面单元得出以下关系:
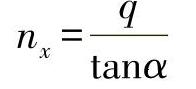
由此,可以计算出一个场的变形能[3],并通过求导与置零,最后消除皱褶角。变形能的分量(参见8.4节)可如下计算:
●由两个支柱有(有Qp/2和Ap/2):

●由两个弦杆有:

●由板材有:(https://www.xing528.com)

现在,须将上面这些分量合并为总的变形能。为此,可有目的地引入以下两个简化式:

也可以经过适当地变换,生成以下三角函数式:

则总的变形能为
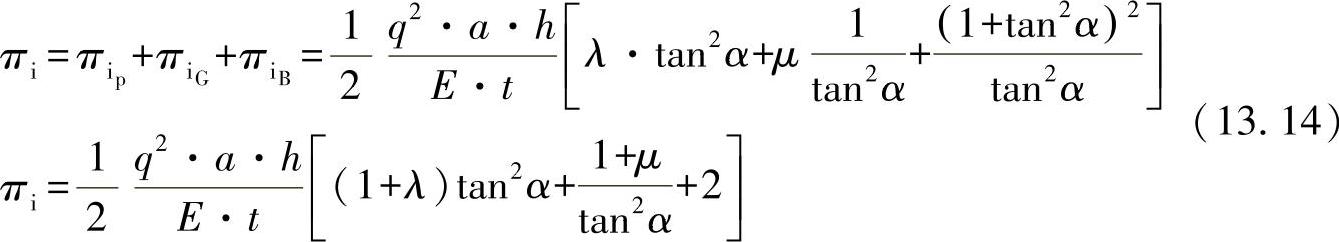
在平衡状态下,变形能达到最小值(卡氏第二定理):

由于这里只有括号内的表达式可以消除,则还应有条件为

即:

由于对薄板材有λ<1、μ<1,在第一近似中tanα≈1,则皱褶角为α≈45°,如图13-5所示。
为了得出皱褶角为45°时的实际偏差,可将偏差代入一个误差方程中:

这里,Δα是一个非常小的角。这样可得出:

考虑到:
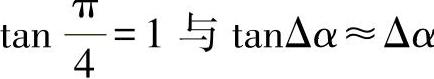
有:

图13-5 tanα的变化
对方程式(13.16)进行类推,可以得出:

还有一致性:

则可得出:

从本质上来看,偏差角是板材几何尺寸与杆的设计参数的一个函数,也就是剪场刚度的函数。
[1]sin2α=2sinα·cosα。
[2]参看第19章中板材的“凸起”部分与DIN 4114。
[3]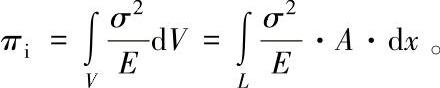
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




