【摘要】：在考虑与横截面应力载荷分析直接相关的问题时，必须要考察任意横截面的几何特征值。在图11-2所示的型材横截面例子中，应当给出一个可能的解决方法。基本的考虑是，用长度为Δsi和厚度为Δti的矩形单元将横截面进行分割。这些矩形单元的位置由回转坐标si和场坐标yi、zi给出。根据以上假设，可得出在k单元给出的近似横截面的面积为图11-2 横截面上几何特征值的确定由此，可确定重心坐标，并列出如下重心公式：另外，还可求解面积惯性矩。
在考虑与横截面应力载荷分析直接相关的问题时，必须要考察任意横截面的几何特征值。由于这一问题首次在本章节中出现，为此，须先在过去的章节基础上给出一些前提条件（静态力矩、剪切中心）的定义。
在图11-2所示的型材横截面例子中，应当给出一个可能的解决方法。基本的考虑是，用长度为Δsi和厚度为Δti的矩形单元将横截面进行分割。这些矩形单元的位置由回转坐标si和场坐标yi、zi给出。
根据以上假设，可得出在k单元给出的近似横截面的面积为
图11-2 横截面上几何特征值的确定
由此，可确定重心坐标，并列出如下重心公式：
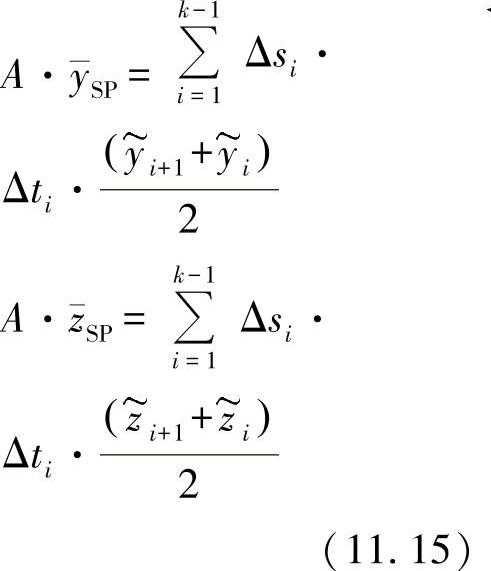
另外，还可求解面积惯性矩。对于这里推导出的方法，首先要求进行先期的考察。为此，可以由两个广义函数f（s）、g（s）得出，在积分区域s=si至s=si+Δsi之间是线性的。为了有效表示函数，可规定如下：
由此，在极限范围内，可通过如下的线性近似得出：
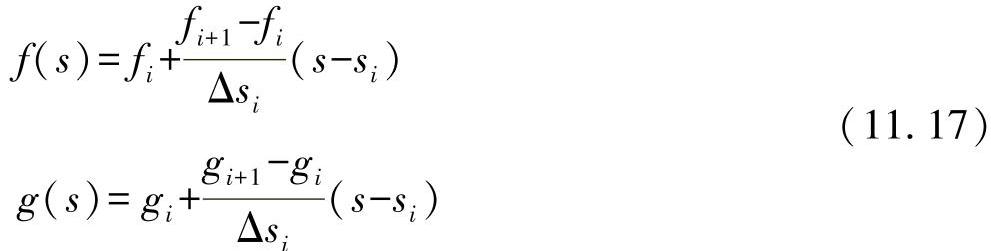
对于后面必要的对面积惯性矩的积分，利用现有的函数可有如下积分：
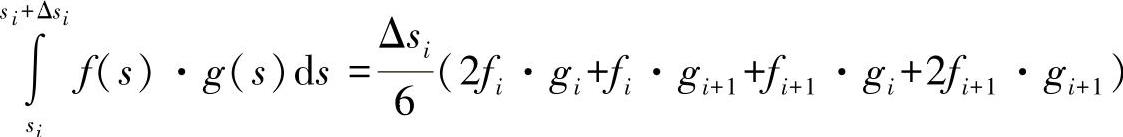(www.xing528.com)
照此方式，可给出矩形单元的面积惯性矩为
相应地有：
相加后，可得出总惯性矩为
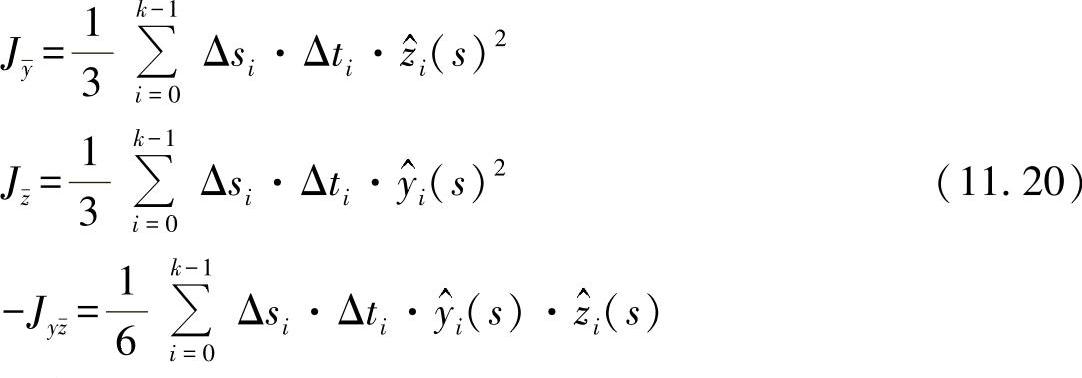
采用同样的方法，可求出静态力矩为
因此，可进一步求出剪切中心的位置为
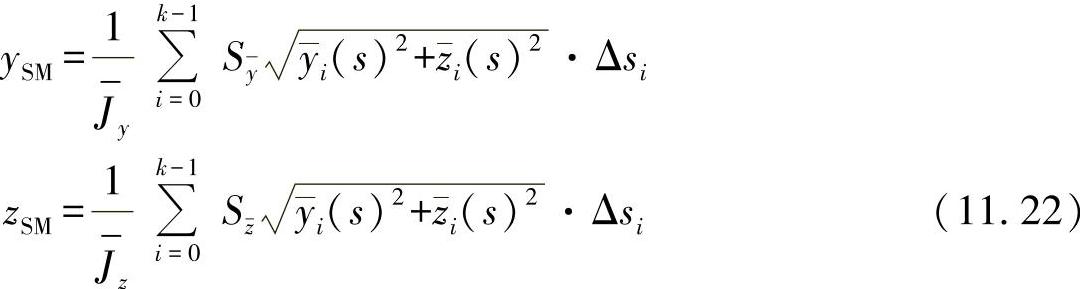
由于有算法，很容易对上面的方法进行编程。根据这些方法，可以评估任意几何形状的型材。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
