广义法向应力问题解决方案

在下面显示的型材横截面上，假设由一个力组F_x、F_y、F_z组成的负载，通过内力产生载荷。每一种载荷类型都产生了一个线性应力载荷分布，如图11-1所示，图中的变化适用于应力与应变的情况。

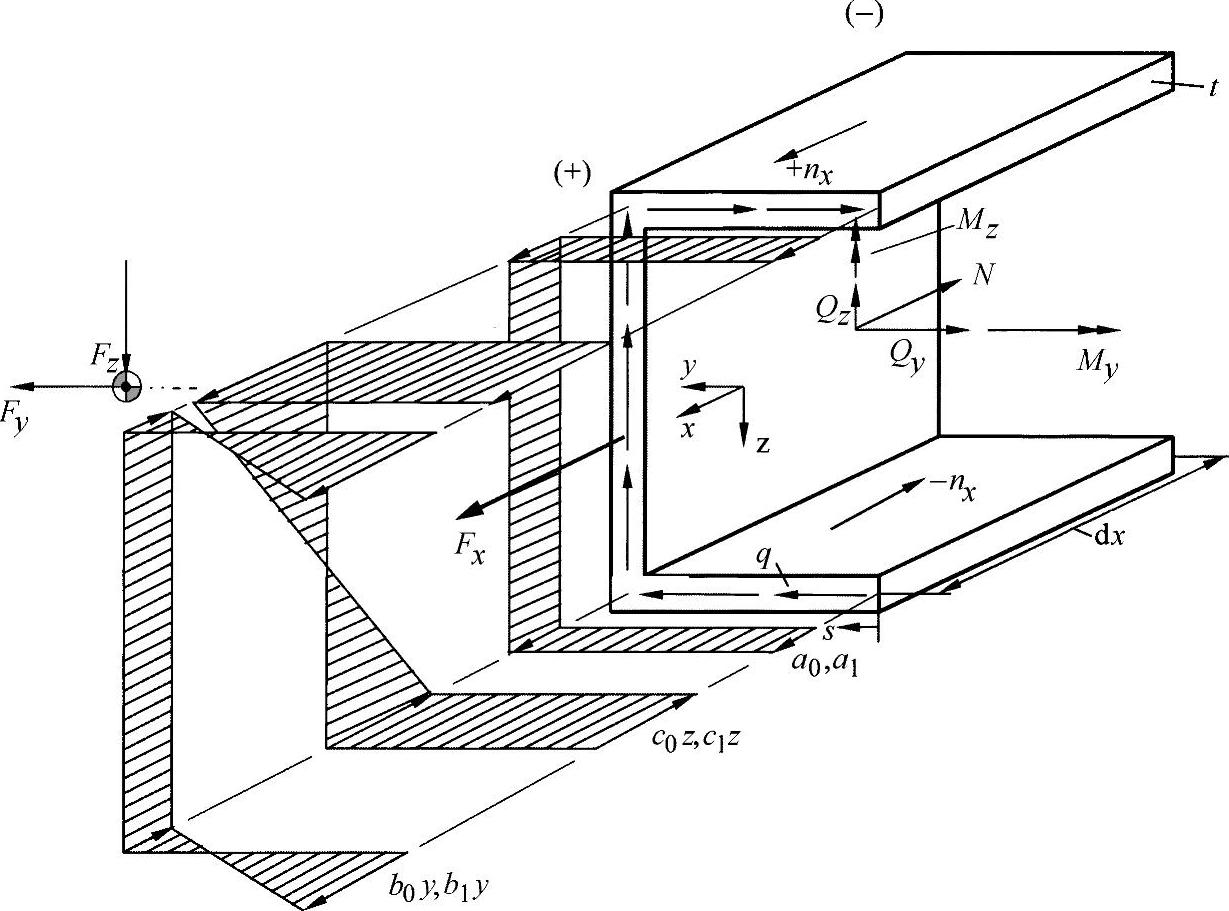
图11-1 在开口型材上，F_x、F_y、F_z力组作用下形成的法向应力状态

对于受力产生的总应变过程，可用下述线性表达式[CZE 67]表示：

ε_x=a₀+b₀·y+c₀·z （11.1）

这里假设的应变系数a₀、b₀、c₀只与轴向坐标x有关。如果进一步假设材料行为是线弹性的，则产生的法向应力一般可如下计算：

σ_x=E·ε_x=E（a₀+b₀·y+c₀·z）≡a₁+b₁·y+c₁·z （11.2）

应力系数a₁、b₁、c₁与前面的应变系数成比例。

通过上面的计算，可以得出最后作用在型材上的法向力流。根据定义，法向力流可线性计算如下：

n_x=σ_x·t=a₁·t+b₁·t·y+c₁·t·z （11.3）

考虑已经在方程式（9.8）中表示出的内力变量与法向力流之间的内在关系，则对在U形型材上体现出的比例关系可确定如下：

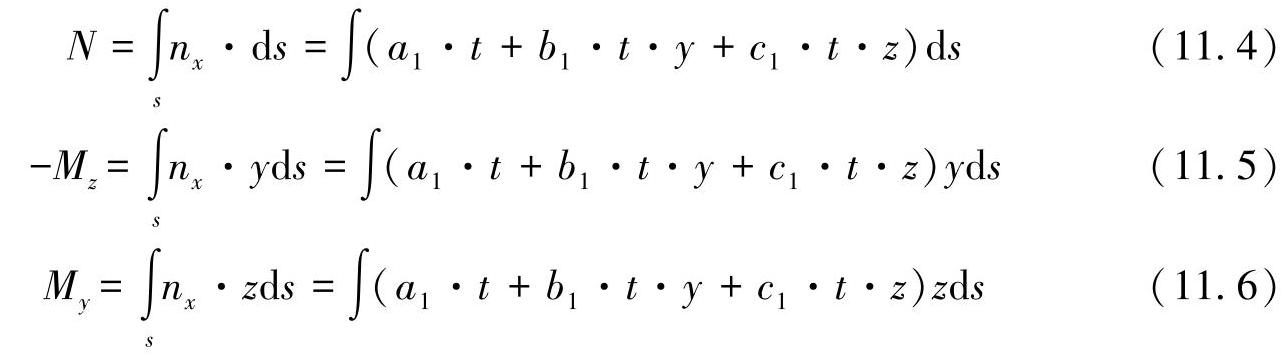
现在要由上述三个方程式来求出三个未知的系数a₁、b₁、c₁。为此，可以有目的地推导出如下的线性方程组（见8.2节），其中，预因子的系数和已知的力可以分开：

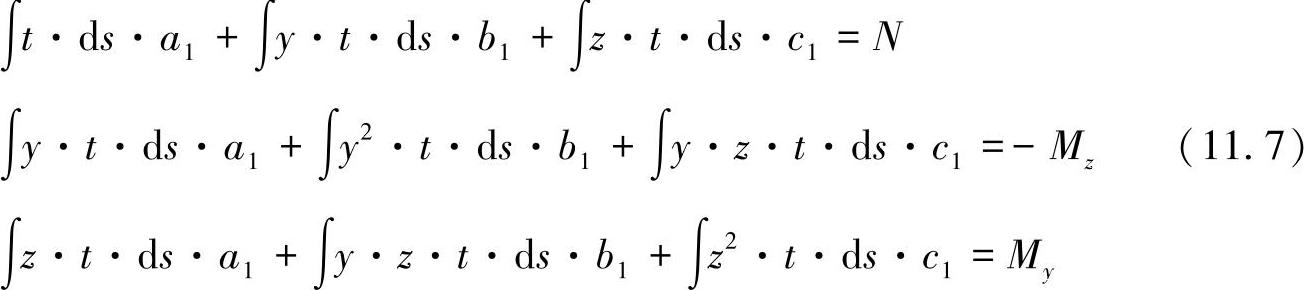
在该方程组中，又可以看到几个熟悉的表达式，在前面已经将其定义为几何特征值，即：

●面积 A=∫t·ds

●静态力矩 S_y=∫z·t·ds，S_z=∫y·t·ds

●面积惯性矩 J_y=∫z²·t·ds，J_z=∫y²·t·ds

●偏转力矩 -J_yz=∫y·z·t·ds

在生成与求解上述方程组时，特别要考虑到描述开口型材时已有的比例关系：

情形1：存在一个广义的不对称横截面。为了描述其几何特征，需要一个带有任意位置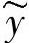、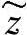的坐标系。对于方程组（11.7）来说可以确定，这

三个方程是耦合的，必须按照a₁、b₁、c₁来求解。

情形2：存在一个点对称横截面（Z形型材）。为了描述其几何特征，将坐标

系放在重心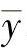、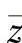上。

对于第二种情形，首先由重心的定义（静态力矩消失）得出：

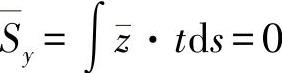
与

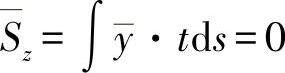
方程组（11.7）可削减为

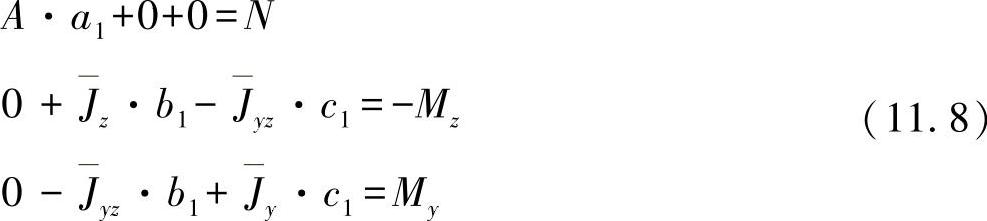
并可立即求解，则求得系数为(www.xing528.com)

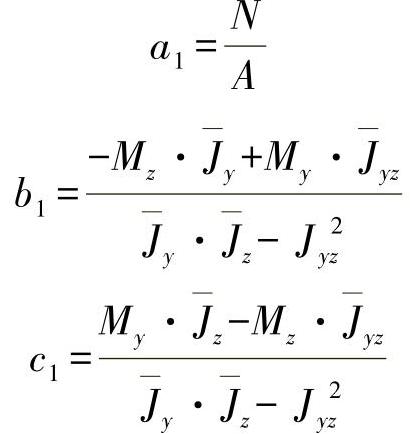
根据以上结果，按方程式（11.2）可确定出现的应力为

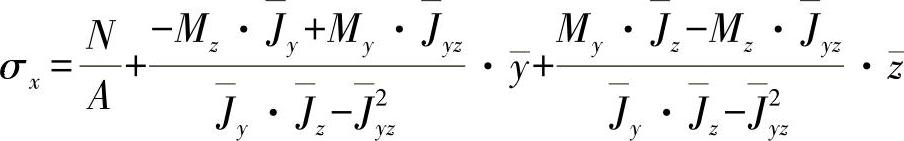
或者对方程式经过整理，可有：

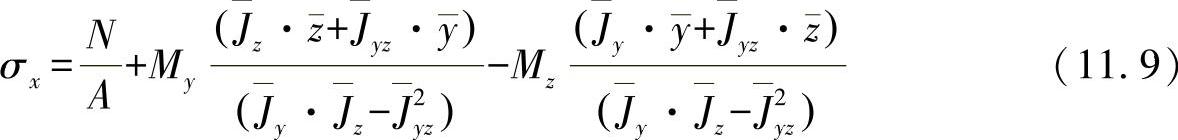
从该方程式中可以看出，应力是如何计算出来的；另外，也可以看出，对于叠加的法向应力，叠加原理不适用于其简单的形式。

情形3：存在一个简单或者双对称横截面（U形、I形）。在这种情况下，重心

坐标系与型材的主轴重合，并有J_y≡J₁与J_z≡J₂。

对主轴系来说，在这里，偏转力矩消失了：

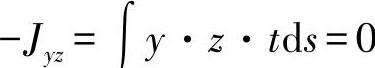
由此，方程组（11.7）可进一步简化为

A·a₁+0+0=N

0+J_z·b₁+0=-M_z （11.10）

0+0+J_y·c₁=M_y

从以上方程组可看出，再没有相互耦合的情况了。由：

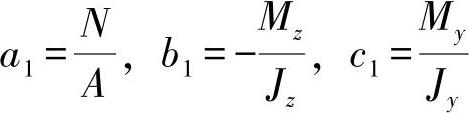
即可得出应力为

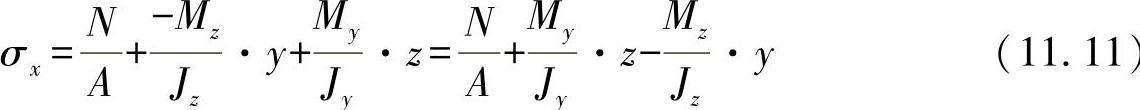
其中，y和z为相应的边缘纤维距离。

适用于实际计算的重要方程的前提条件为

●线弹性行为；

●任意开口横截面几何形状，在轴向上的面积恒定。

由于通过方程式（11.3）可立即得出法向力流n_x，所以，应当可以完整地导出剪力变化过程q。为此，可利用方程式（9.4）中已知的差分关系，将方程式（11.11）用于展开的笛卡儿坐标系的对称轴中。

对于通常无变化的法向力（N=常数），可对应力表达式进行求导：

如在图11-1中所看到的，这两个弯曲力矩与纵向坐标x相关。因此，可以得出剪力流为

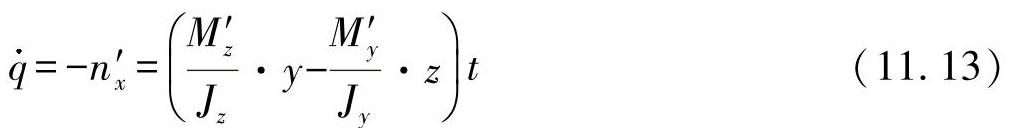
由相对应的积分，可得出：

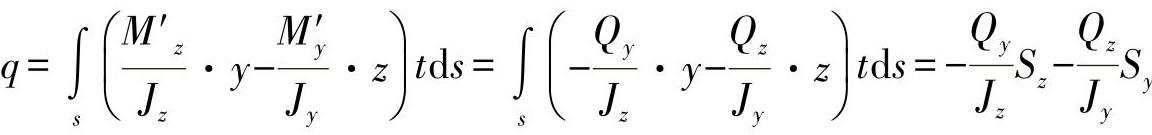
值得注意的是，得到验算的表达式与初始确定的力的方向有关。