翘曲阻力的简单材料应用

前面已经证明了，两凸缘或者三面型材可以发生翘曲，因此对这类型材的使用要加以特别的注意。常用的属于这种类型设计的型材有：

●双T形型材。

●U形型材。

●Z形型材。

下面以示例说明，如何来确定这些横截面形状型材翘曲阻力的大小。

●图10-9a首先描述了在小变形下I形型材上的几何关系。由扭转可得出对ϕ的整个横截面扭转。因此，凸缘的位移为

现在假定，存在无阻碍翘曲，则根据方程式（10.40），轴向翘曲位移为

u≈-v′·y （10.45）

上式中，忽略了剪切变形。根据凸缘单独扭转引起的翘曲，可进一步导出等效的凸缘力矩：

凸缘中的翘曲应力大小为

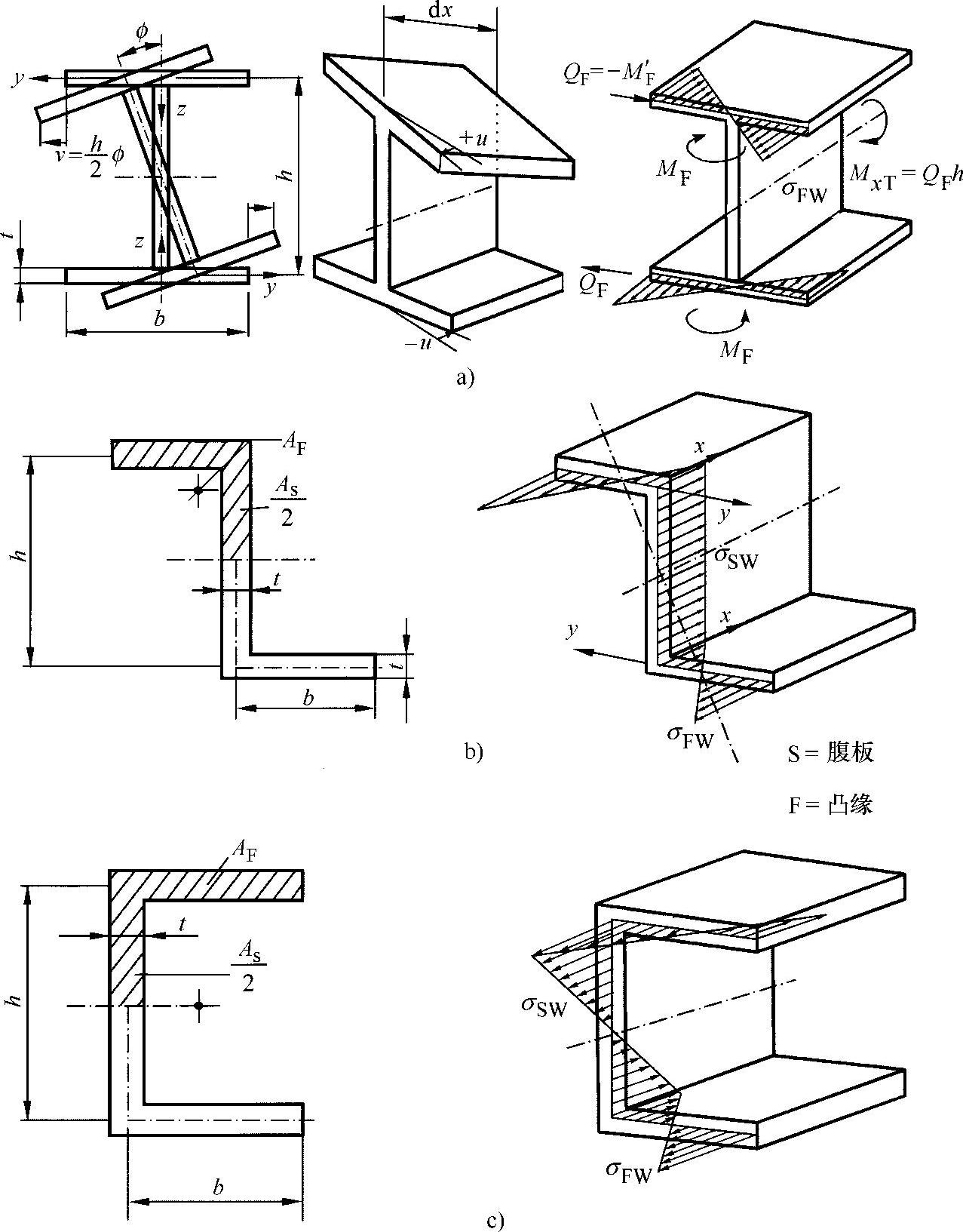
图10-9 型材的翘曲[WIE 96a]

a）双对称I形型材 b）点对称Z形型材 c）简单对称U形型材

σ_FW=E·u′≈-E·v″·y （10.47）

采取同样的方法可得出凸缘力矩为

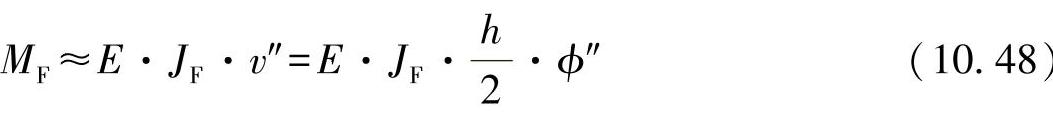
这些围绕z轴弯曲的力矩在两个凸缘上大小相同，但是方向相反。力矩通过凸缘的间距形成一个轴向双力矩：

只有通过剪切力，才能使这个双力矩发生变化。据此可得：

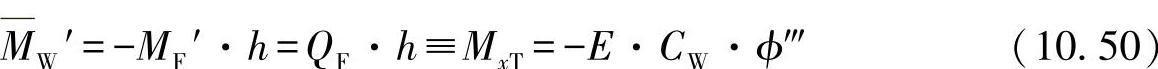
研究上式与式（10.48）的关系，可得出：

根据上述结果，可得出翘曲阻力为

其中：

(www.xing528.com)

作为围绕应力载荷轴的凸缘面积惯性矩而代入方程式。

●另外还存在带有不相同凸缘的I形型材，即有不相同面积惯性矩的I形型材，在这种特殊情况下的翘曲阻力为

●图10-9b展示了一个Z形型材。与I形型材相反，Z形型材由翘曲产生的应力载荷会一直传播到腹板上。不用求导，即可得翘曲阻力为

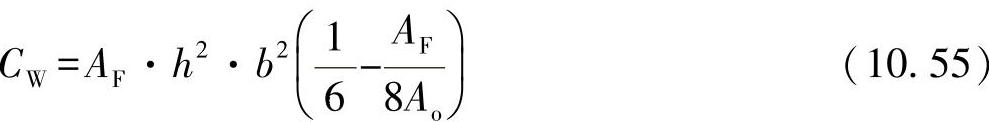
其中：

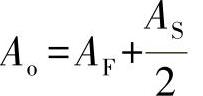
●图10-9c中表示了在U形型材上的比例关系，其重要的标识为反对称应力分布。不需求导可得翘曲阻力为

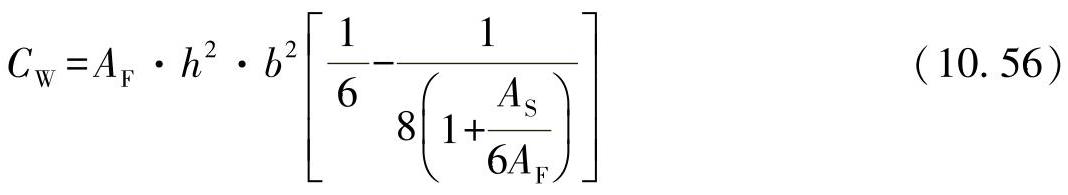
对于前面研究的型材，在腹板面积与凸缘面积相比很小的情况下，可在所有三面型材上非常近似地计算出翘曲阻力为

最后再相互计算以上四种形状型材的翘曲阻力，在所有边与壁的壁厚相同的条件下有：

即相对来说，I形型材的翘曲阻力最小。相比之下，U形型材的翘曲阻力是I形型材的1.75倍，Z形型材的翘曲阻力则是I形型材的2.5倍。

对于刚度要求尽可能高的设计参数，可考虑如何利用h/b的比例关系来计算翘曲阻力的最佳值。为了对这个问题进行研究，可简单假定，腹板对翘曲阻力无影响，且壁厚t=常数。考虑到材料消耗（展开：a=2b+h，a_R=2b+2h）并考虑到对某种形状型材适用的翘曲阻力，可得出：

亦即针对型材的相关表达式为：

●I形：

●Z形：

●U形：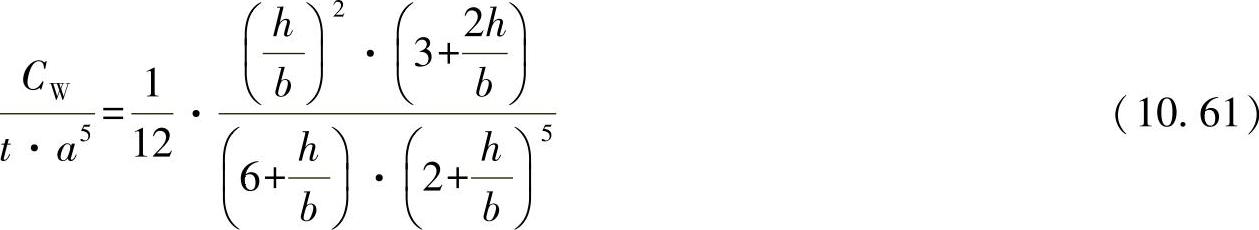

●

:

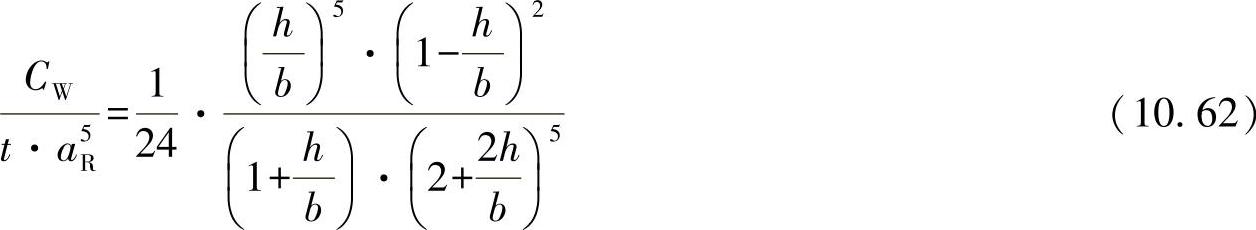
相关的翘曲阻力描绘图如图10-10所示。从曲线中可得出凸缘宽度对应于型材高度的最佳比例关系，其翘曲阻力为极限值。

图10-10 双凸缘型材的相关翘曲阻力，考虑到展开以及材料利用的优化[WIE 96a]

[1]假设为，在承受扭转应力载荷的型梁中只出现一个纯切应力状态。由于存在无约束支座，没有法向应力。