横截面翘曲的产生及表现

前面已经得出，非圆形横截面的剪切应力载荷及扭转应力载荷与翘曲是联系在一起的。翘曲可以理解为整个横截面的挠曲。在这个意义上，“翘曲的前提是，一个初始水平横截面至少有四个点发生了相对移动，使得平面无法再保持与轴向平行”。对于所有矩形角型材来说，这意味着至少要有三个分型面。不过也有无法定义翘曲的型材，如图10-7的示例，这些型材都可看做是无翘曲的。

●两个分型面的T、L形辊轧型材和星状挤压型材。

●三角形型材，逐段壁厚都不相同。

●圆形正切多边形，壁厚为常数。

●矩形型材，壁厚比例。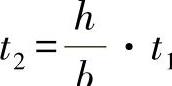

图10-7 无翘曲开口与闭口设计型材[BRU 84]

现在横截面上发生翘曲，该翘曲受阻于横截面的拉紧，因此产生了附加的法向应力。为了求解该应力，须列出法向应力方程：

这里出现的参数M_W为内力变量，可标识为轴向双力矩。ω^*可标识为围绕剪切中心的翘曲函数。由：

∫ω^*2·tds=C_W （10.35）

可在剪切中心上引入相应的翘曲阻力。

扭转一个可翘曲的型杆，则型杆所传递的扭转力矩可分解为：

●由圣维南（纯）扭转导致的M_xt分量^[1]。

●由翘曲剪切力流导致的分量。

据此，有以下平衡方程：

M_x=M_xt+M_xT

这里，翘曲力矩可定义为

M_xT=∫n_x′·ω^*·ds （10.36）

因此，由翘曲产生的轴向应力[见式（10.34）]为

由此应力引起的法向力流变化[见式（9.1）]可确定为

现在，如果考虑到这个内在关系，并且考虑到式（10.35），最后可得出翘曲力矩为(www.xing528.com)

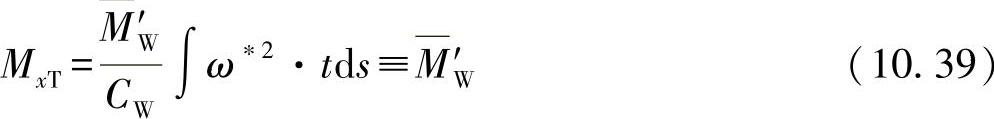
即翘曲力矩由对轴向双力矩求导得出。为了确定翘曲力扭转的基本公式，须先定义变形条件。为此，在图10-8中描述了一个U形型材的翘曲表层部分。

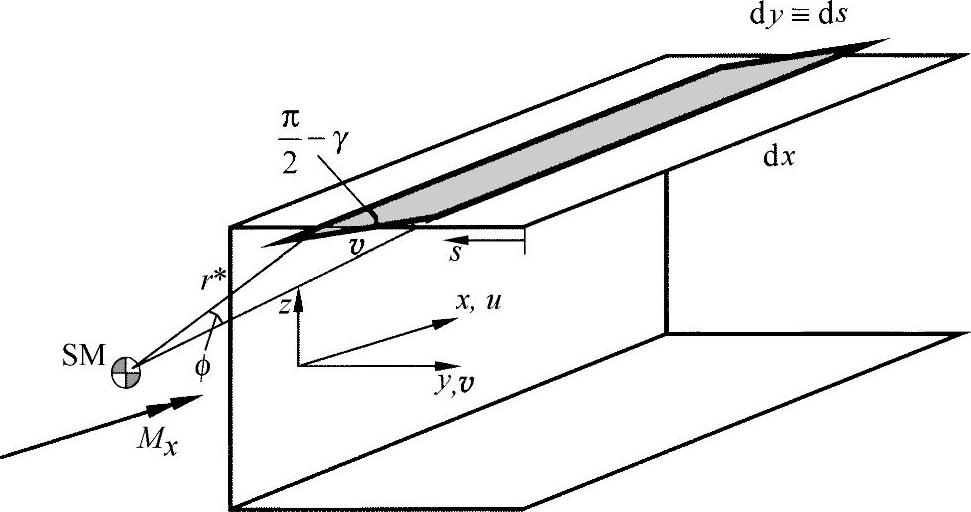
图10-8 U形型梁的横截面翘曲

翘曲表现为由横截面平面凸出来的表面部分。由扭曲关系可得出：

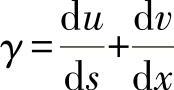
根据上述计算结果可求出从平面发生的位移：

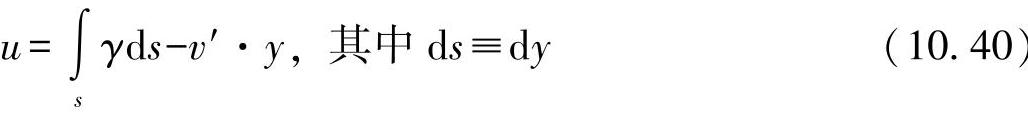
与剪切中心相关的作用在平面上的位移v为

v=r^*·ϕ

由此可直接确定由翘曲产生的应力为

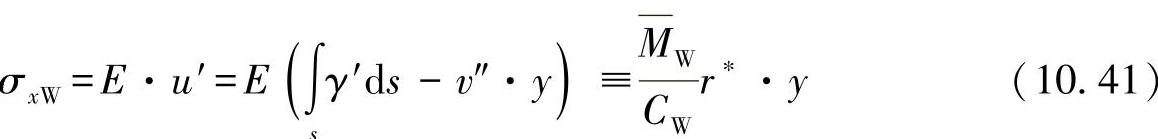
如将下式代入翘曲函数：

r^*·y=ω^*

求解式（10.41），则可得轴向双力矩为

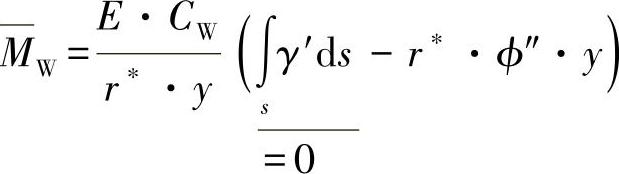
计算中通常可忽略由剪切变形产生的角变化，因此，上式可简化为

考虑到式（10.39），有如下定义：

从该方程中可得出扭转角第三导数的比例。考虑到式（10.3），则翘曲力扭转可通过下面不均匀微分方程得出：

E·C_W·ϕ‴-G·J_t·ϕ′=-M_x

对于这类方程组（参见练习4），可较容易设计出均匀的（ϕ_h）与（ϕ_p）的部分解法，这里扭转角和力矩分量也是已知的。