空心横截面带腹板的轻量化设计

为了提高刚度，绝大多数的空心横截面都带有中间腹板。这样可以构建起单元格，每个单元格的内力矩都会对外力矩的平衡起到相应的作用。

为了清晰说明起见，下面只研究图10-6所示的简单的三单元格型材。对于与此例不一样的型材，可对解法加以适当修改。实际中的多单元格型材应用示例为机翼或者机车的地板组（如：ICE2和ICE3）（ICE为德国铁路的城市间高速机车Inter-CityExpress的缩写，译者注）。

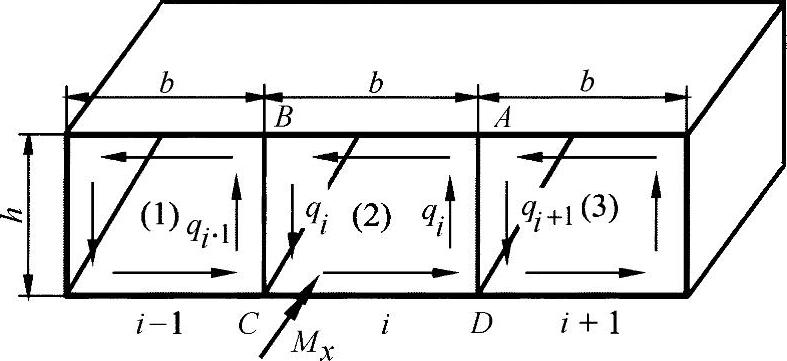
图10-6 在扭转作用下，通过中间腹板分割的空心型材

在下述简化的前提条件下：

●无约束扭转。

●每个单元格中的剪切力流q_i为常数。

●小变形。

可假设所有单元格承担相同的力矩传输，则可得出：

为了计算三个剪切力流，只有这个假设是不够的；因此，还必须引入变形条件。为此可进一步假设，所有的单元格承受同样的扭曲：

ϕ′₁=ϕ₂′=ϕ′₃=ϕ′=常数

据此，可计算出每个单元格的力矩：

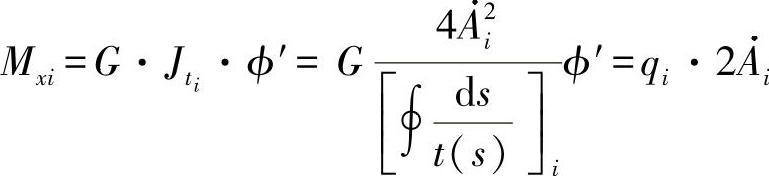
这一推理适当地证明了，现有的公式可如下进行转换：

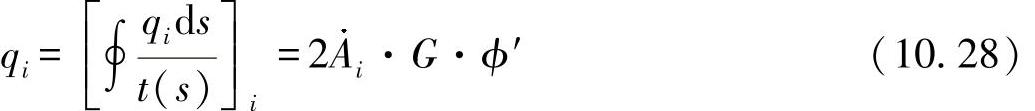
举例来说，如将三个单元格的中间值表示为i，则式（10.28）可如下展开：

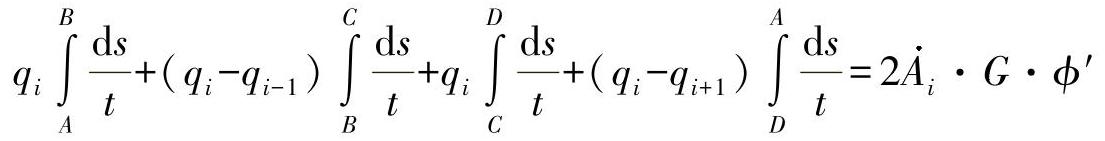
适当合并相应的项有：(www.xing528.com)

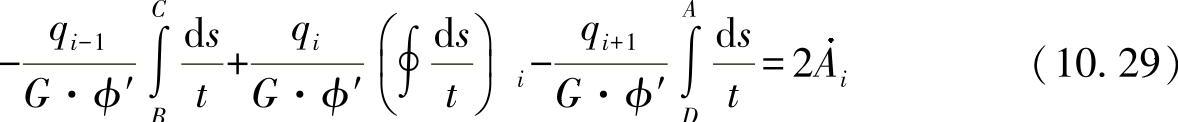
代入以下的缩写更有意义：

并且

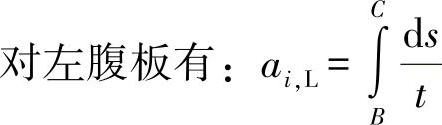
对整个单元格有：

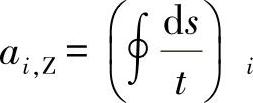
对右腹板有：

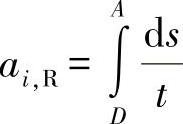
出于弹性考虑，可以证明，对称横截面的系数也是对称的，即有：

a_i，L=a_i-1，R与a_i，R=a_i+1，L

由此，可整个将方程式（10.29）整理为

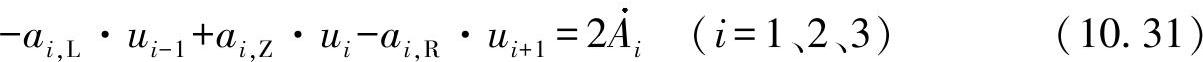
对于三单元格型材，可提出方程组：

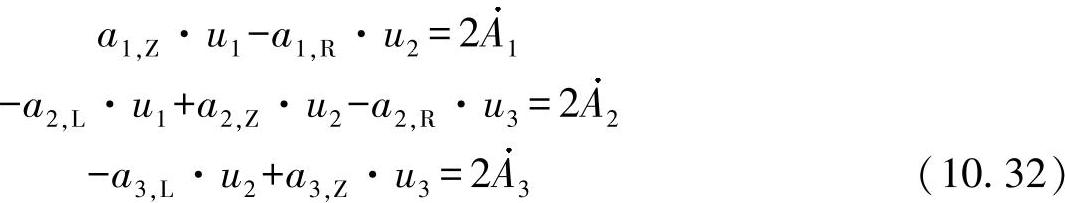
因此，可确定未知的u₁、u₂、u₃。借助式（10.30），根据逆算法，可求得剪切力流q_i（i=1、2、3）为

q_i=（G·ϕ′）·u_i （10.33）

举例来说，对于中间部分横截面，此处的ϕ′可由式（10.14）确定。