【摘要】:图10-1显示了杆单元上的比例关系。对于圆弧b依据几何关系有:图10-1 在型杆单元上的扭转作为线性问题γ·dx=r·d 或者:这里′为扭曲,对应于扭转。由此,可给出弹性定律:τ=G·γ=G·′·r≡G·D·r 该定律描述了在横截面上的线性应力分布。上式表征了圆形横截面无约束扭转的关系。乘积G·Jt与滑移模数一起表明了横截面的扭转刚度。
按照圣维南基本扭转理论,在圆形横截面情况下可假设,扭转力矩作用于杆轴上;在这一载荷作用下,横截面保持在水平面上,不发生翘曲(横截面挠曲),杆作为一个整体可相对无约束地旋转。在这种情况下,只产生剪切应力载荷。
图10-1显示了杆单元上的比例关系。在小变形的前提下,即使在“扭转”D作用下,母线也保持平直。对于圆弧b依据几何关系有:

图10-1 在型杆单元上的扭转作为线性问题
γ·dx=r·dϕ (10.1)
或者:
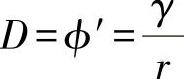
这里ϕ′为扭曲,对应于扭转。由此,可给出弹性定律:(https://www.xing528.com)
τ(r)=G·γ=G·ϕ′·r≡G·D·r (10.2)
该定律描述了在横截面上的线性应力分布。外载荷必须与这一应力分布保持平衡,也就是说:

式中,Jp代表极面积惯性矩。
上式表征了圆形横截面无约束扭转的关系。对于所有非圆形横截面,则用与横截面相关的几何值Jt代替Jp(Jt≠Jp)。乘积G·Jt与滑移模数一起表明了横截面的扭转刚度。
对于任意横截面,为了产生翘曲,必须放弃保持水平的前提条件,特别是这一翘曲如果受到阻碍的话,在产生扭转载荷的同时,也会产生法向力载荷;在这种情况下,可称之为发生“翘曲力扭转”。
下一步要讨论到应力分布、极几何特征值与由翘曲产生的结果。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




