闭口不对称型材-轻量化设计成果

与前面计算过的开口与闭口型材相比，对于闭口不对称型材的处理要困难得多，因为单凭平衡条件无法确定剪切力流。因此，须首先由一般关系出发：

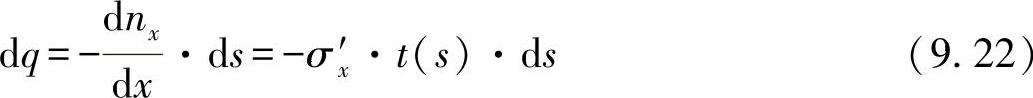
对于纯两轴剪切力弯曲，可假设所引起的法向应力为

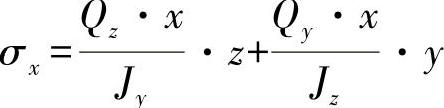
如果对上式求导，可得出：

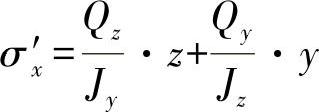
或者代入式（9.22）可得出剪切力流为

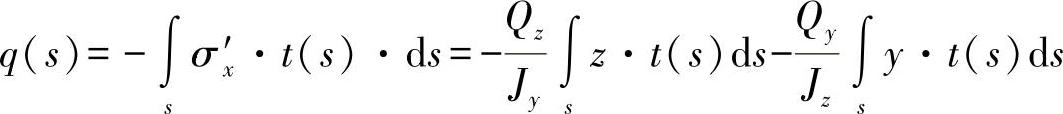
这里又可分离出两个静态力矩，所以最后可得出剪切力流为

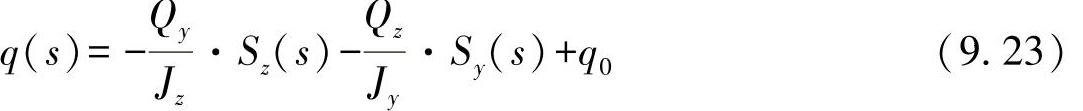
积分常数q₀标识为初始剪切力流。根据迄今为止所研究的情形，即可得出：

●在开口型材的自由边界上总是有q₀=0；

●同样的，在闭口型材的对称轴上也有q₀=0。

在任意闭口不对称型材中，回转常数s的位置是自由的，所以无法预先得知初始剪切力流值的大小。为了进一步确定剪切力流值的大小，须先返回到变形条件。为此，将型材纵向剖开。图9-9所示为带有不均匀的剪切力流变化过程的开口型材。

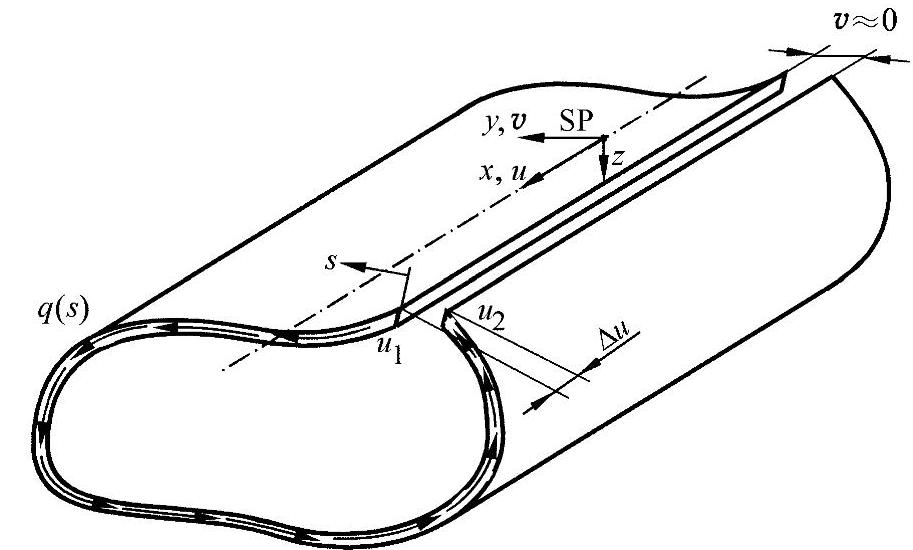
图9-9 开口的不对称型材

在剪切力流的作用下，管的两个边缘相对发生了移动。假设在没有发生位移的面积上正好也有很多面积分量发生了凸出或者凹进，则可计算出：

这里出现的剪切扭曲在前面[见式（9.19）]已经定义为

所以，式（9.24）也可写为

如果用下式替代滑移：

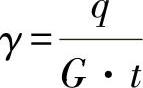(www.xing528.com)

则最终有：

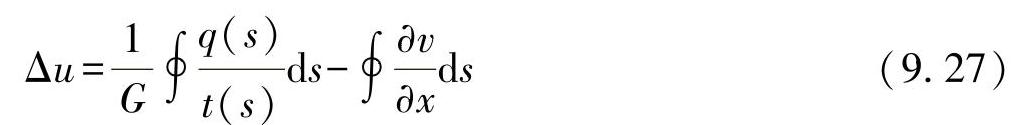
由于截面端应彼此尽可能不移开，所以第二个积分也就消失了。如假设Δu=0，如同闭口型杆的条件，则第一个积分也消失了；不过，其前提是，回转剪切力流q₀与计算剪切力流q（s）相叠加，导致截面端的相对位移也消失。按照这一假设，须有：

由此得出作为常数的初始剪切力流：

对于作用产生的剪切力流，可有：

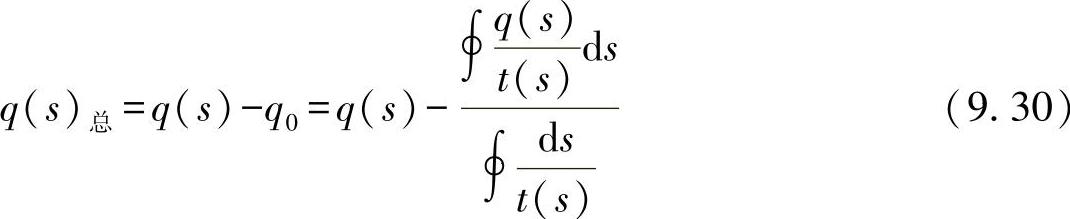
如果在这里代入开口型材的剪切力流，则可得出：

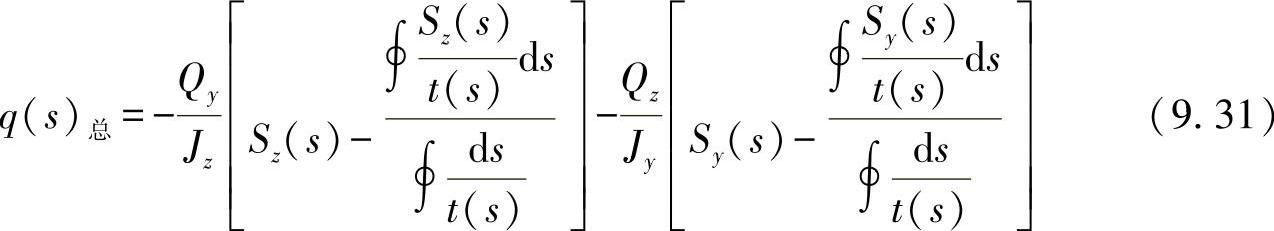
由这一思路可以预想到：对于闭口不对称型材也应当存在一个点，当外力作用在这个点上时，型材不发生扭曲。也就是说，闭口不对称型材也存在一个剪切中心。

图9-10再一次说明了在一个任意横截面上的比例关系。为达到无扭曲状态，要求在内力力矩和外力力矩之间达到平衡：

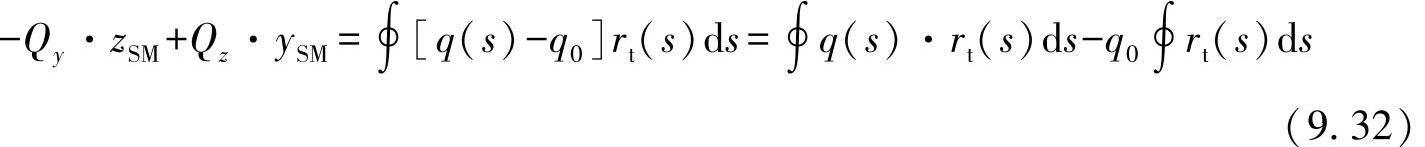
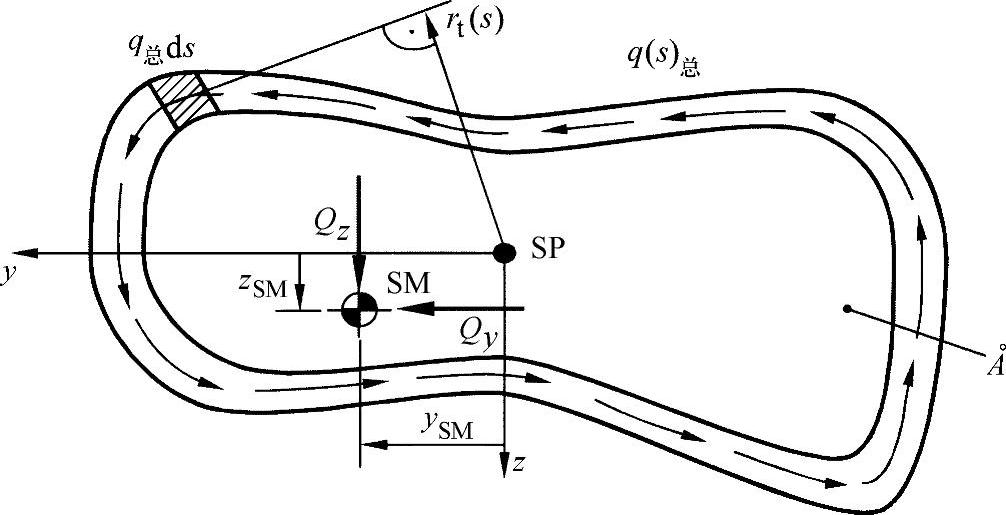
图9-10 在闭口不对称型材中剪切中心点的位置作为突出的受力点

方程式的右侧是环形积分距离乘以圆弧。通过型材中心线看该积分正好是外切面积A的两倍，即：

如果将其作为对q和q₀的已知方程式代入，则由式（9.32）可以得出：

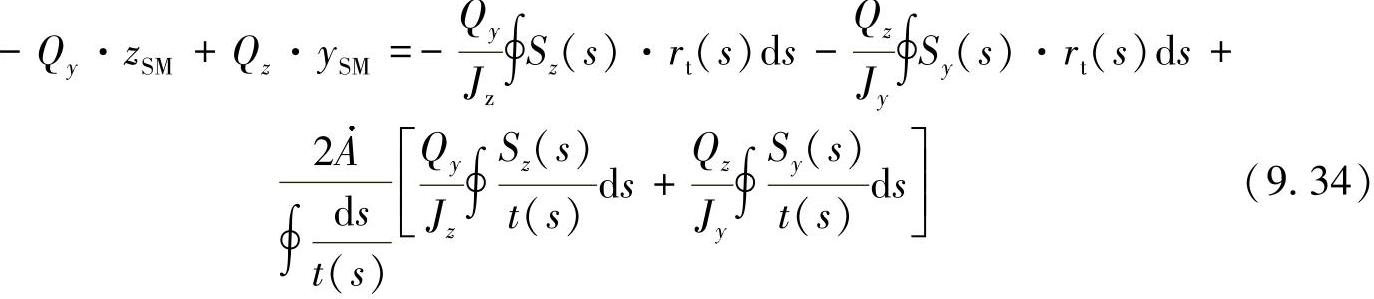
由此，通过简单的系数比较，可得出到中心点的距离为

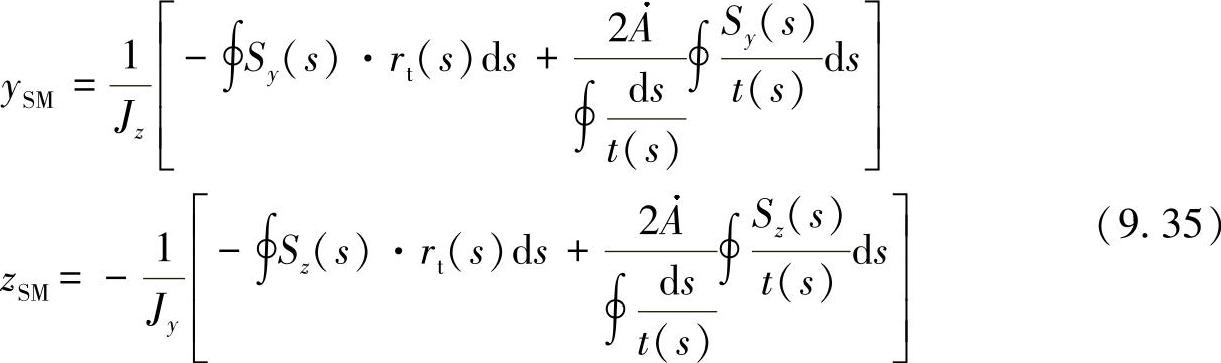
根据以上推理可以证明，即使是在闭口不对称型材横截面的某处，也存在一个可实现力导入的剪切中心点。