开口型材剪切中心位置与力矩平衡

对于开口型材，在方程式（9.13）中提及的初始剪切力流q₀=0。由式（9.12）的力矩平衡可得出：

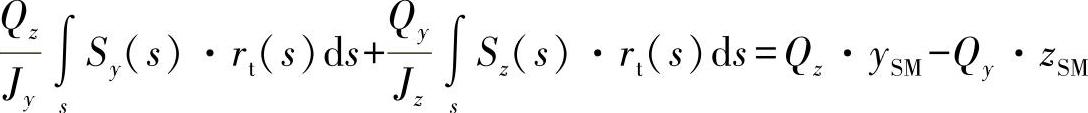
对于剪切力，由相应的系数比较可得出：

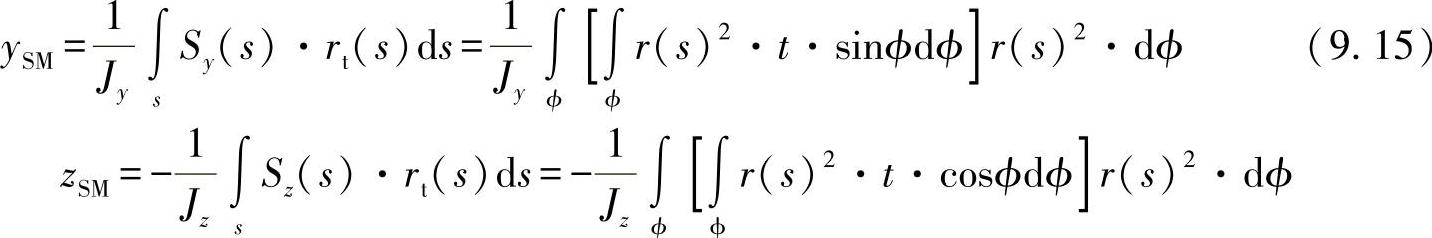
这两个坐标标识了剪切中心的位置。这里，剪切中心就是标识出的点，所有的外力都必须作用于这个点，以确保开口型材不发生扭转。上面的推导都是原理性的，从这个意义上讲，以上推导也可以应用于多直角的型材结构设计。图9-6给出了几个例子。最基本的是在剪切力弯曲作用下的细长矩形型材，其流的定量与定性都是已知的。首先将流代入重心轴，然后在回转坐标上换算：

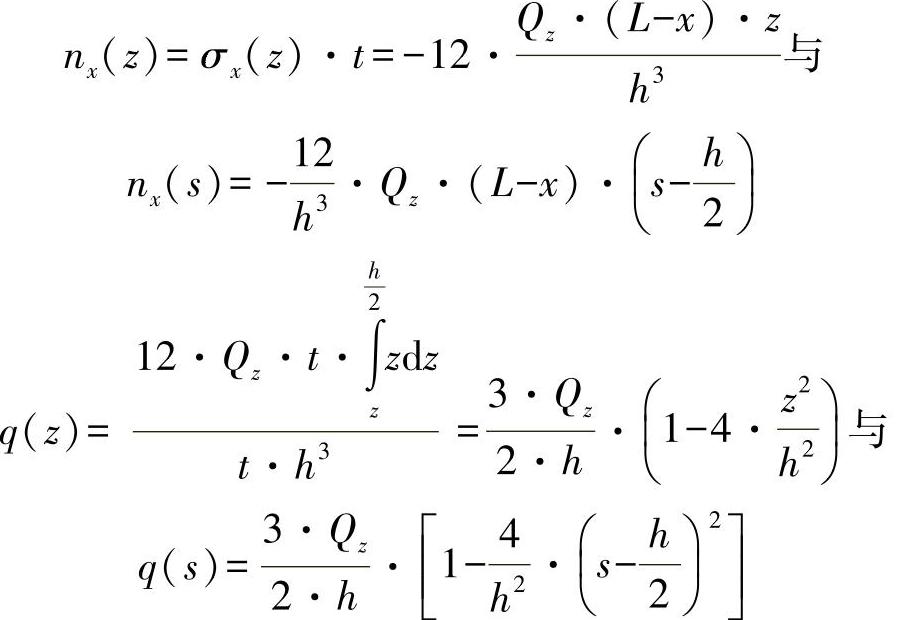
比较棘手的是图中所示的直角板型材情形下的比例关系。考虑到应力情况，这里只讨论凸缘和腹板，并依此确定流。对于法向力流，可以简单有：

n_x（s）=σ_x（s）·t_F，S

或者在忽略腹板的情形下，凸缘上的极大值为

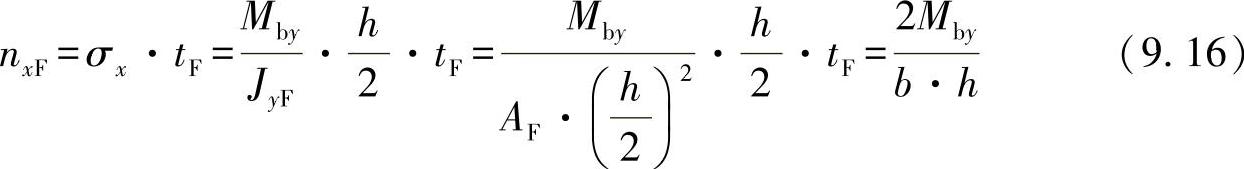
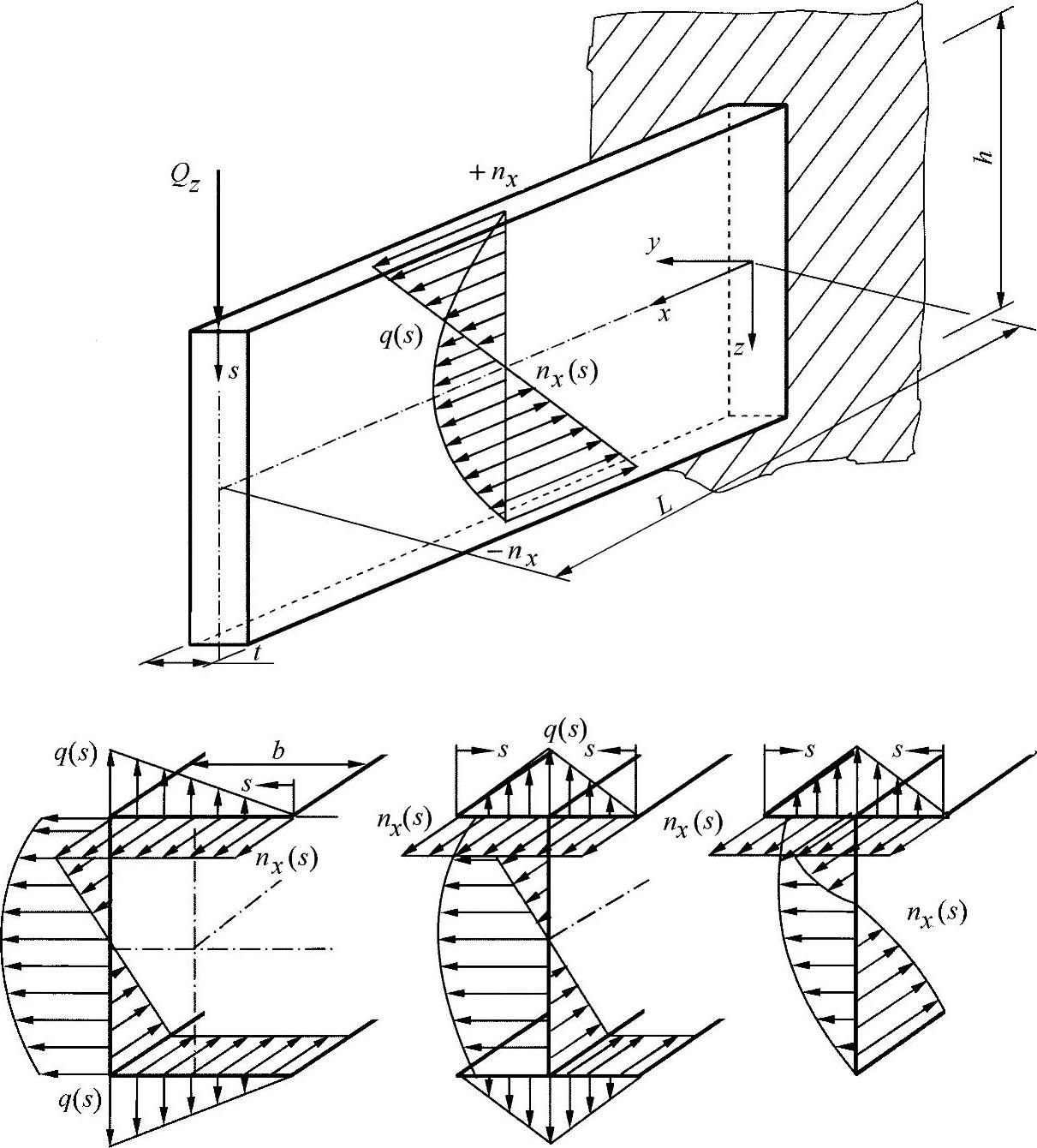
图9-6 薄壁开口型材的流

相应地，可求解剪切力流。为此，从凸缘轴向的自由边界出发，由广义表达式可得出：

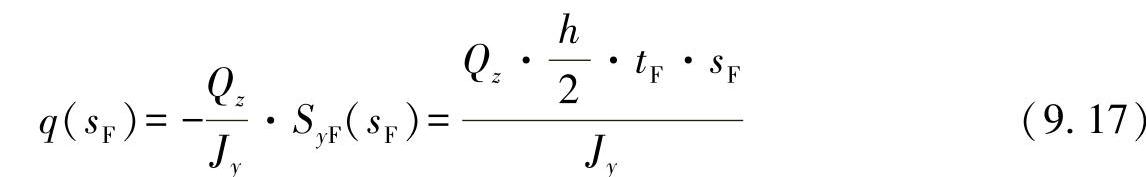
在腹板上，还作用有另外一个坐标s_S=（h/2）-z，相加有：

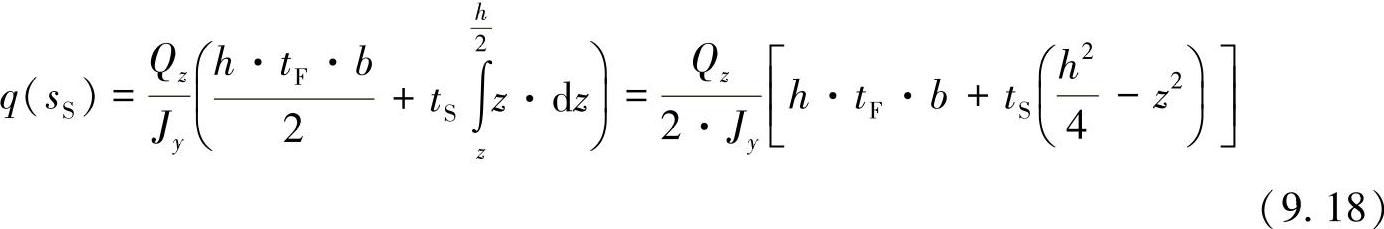
在流的变化过程中，通过所显示的型材横截面，可以清楚地看出方程式（9.4）的作用，它描述了流的相关性。由于在自由边界q=0处的n_x≠0，就是说，出于平衡的原因，剪切力流必增大为法向力流。对于非常薄的型材，可进一步在允许的范围内，根据模型进行简化。其前提是，以下的流的分布占据主要地位：

●在凸缘处 n_xF，q（s_F）=0；(www.xing528.com)

●在腹板处 n_xS=0，q（s_S）=q_m=Q_z/h。

抗剪壁桁梁的情形也可以回溯到这个概念。

作为补充，图9-7显示了几个剪切中心（SM）的位置，可以看到：

●对于简单对称横截面，剪切中心恒定位于对称轴上。

●对于双对称或者极对称横截面，剪切中心位于对称轴的交汇点，与重心重合。

对于回转U形型材，求解式（9.15）可有：

z_SM=0

与

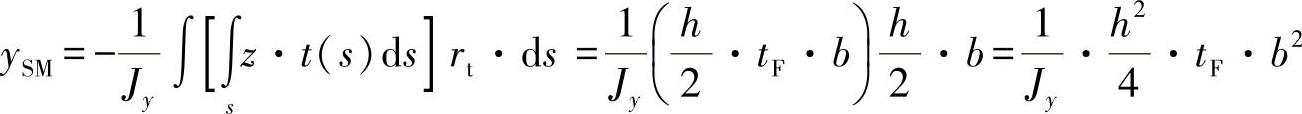
并由：

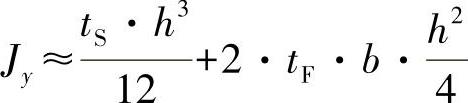
有：

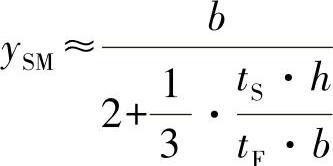
这里考虑到了腹板中心之间的距离。

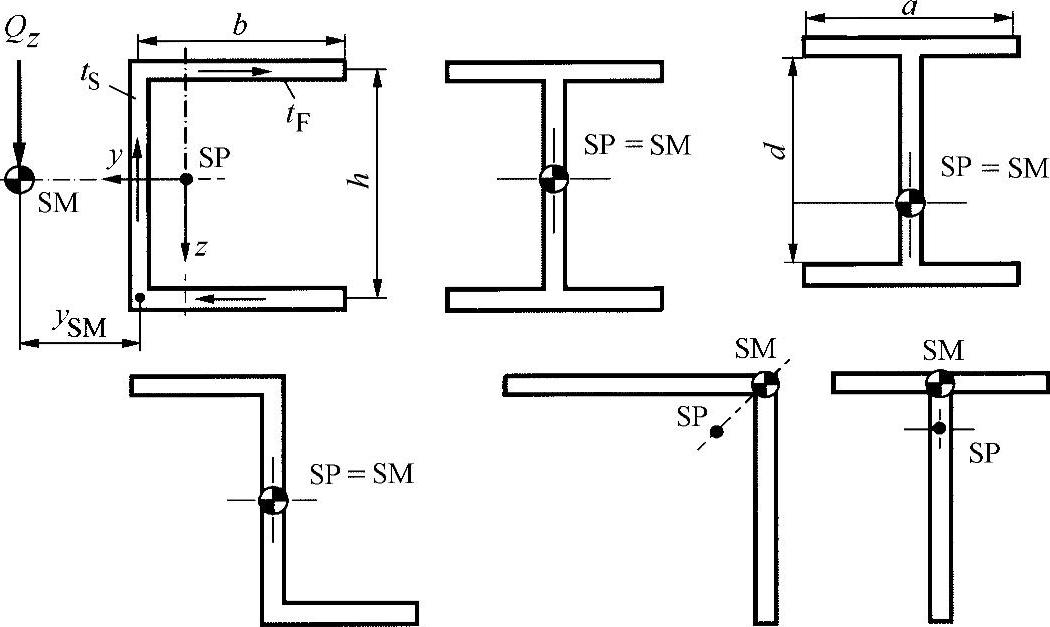
图9-7 几个薄板型材剪切中心的位置