轻量化设计：力流对薄壁弯曲的影响

为了避免特殊情形，图9-1中假设一个任意开口的型杆，型杆上承受一个以轴向为基准的外力组，它由一个轴向力p_x，两个剪切力p_y、p_z和一个由内应力产生的扭转力矩m_x组成。

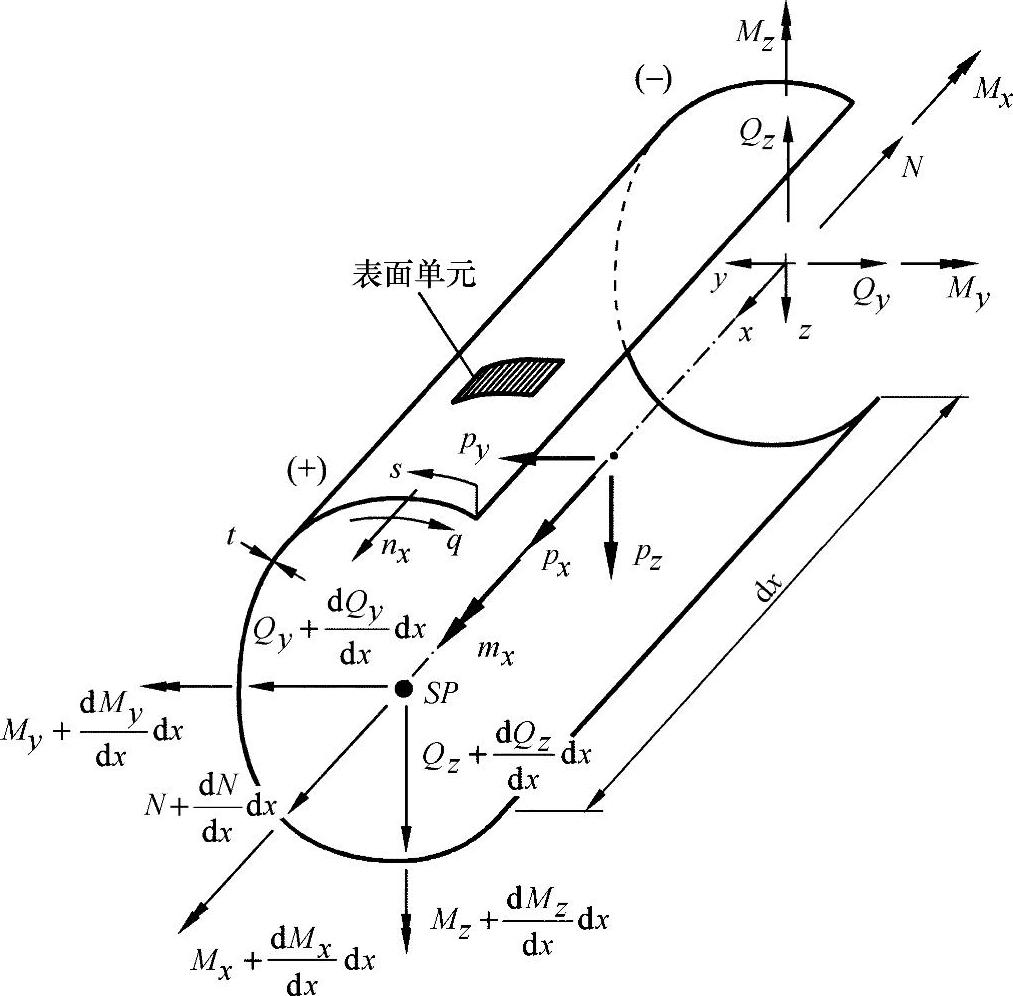
图9-1 开口型杆任意横截面上假定的内力

在8.5节中已经证明，在载荷与内力变量之间存在如下关系：

N′=-p_x

M_x′=-m_x

M″_y=Q_z′=-p_z，M″_z=Q_y′=-p_y

为求得这些应力载荷，在薄壁型材中引入局部横截面之和，即通过切线积分求出的力与应力的和[CZE 67]。由此可以得出以下的广义的内在关系：

●法向应力与所谓的法向力流

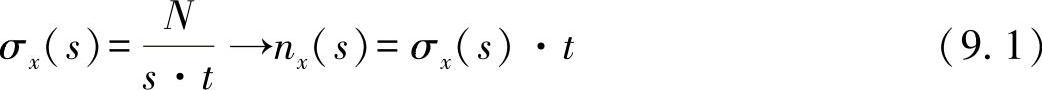
●切应力与所谓的剪切力流

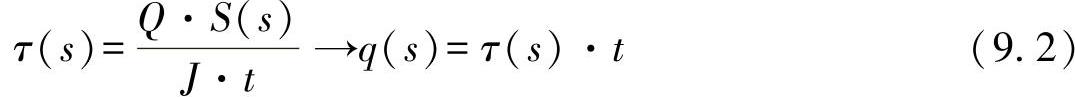
考虑到表层单元的平衡（图9-2），可进一步得出这些力流之间的几个重要关系。

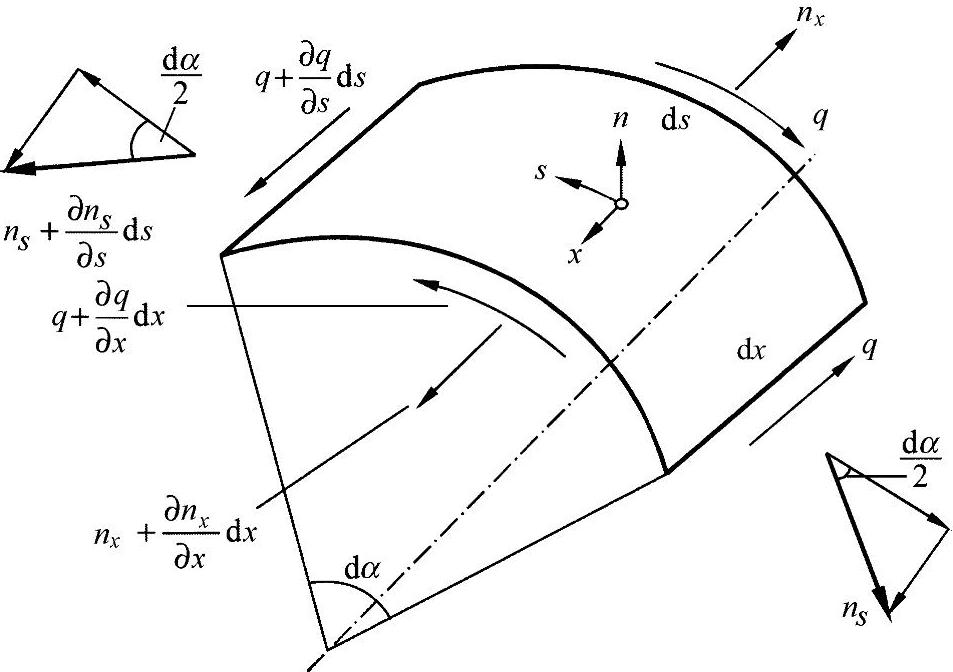
图9-2 力流作用下的薄壁弯曲表层单元（承载型材的广义表面单元） 由三个平衡方程可得：

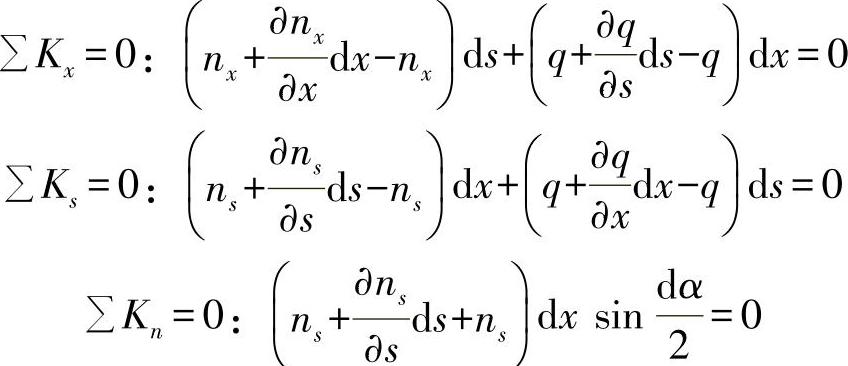
由法线方程式即可得出：

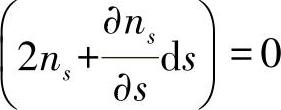
或者由于长度不为零，则只能是：(www.xing528.com)

n_s=0 （9.3）

由另外两个方程式则有：

与

特别是由式（9.5）有：

根据以上推理，可得出以下重要结论[CZE 67]：

●在型杆单元上不产生切线方向上的法向力流n_s。

●在x轴截面上的剪切力流各处大小相同，即q（x）=常数。

●剪切力流q（s）在切线方向上发生如下变化，即剪切力流的增加正好对应于x方向上法向力流n_x的减少。与此相关的方程式（9.4）描述了对于应力载荷的标准关系。

平面表层单元情况的比例关系则有些不同。由于不存在垂直于平面的流矩，不会出现第三个方程。依图9-3，在表层单元n_s≠0，并且产生附加作用。

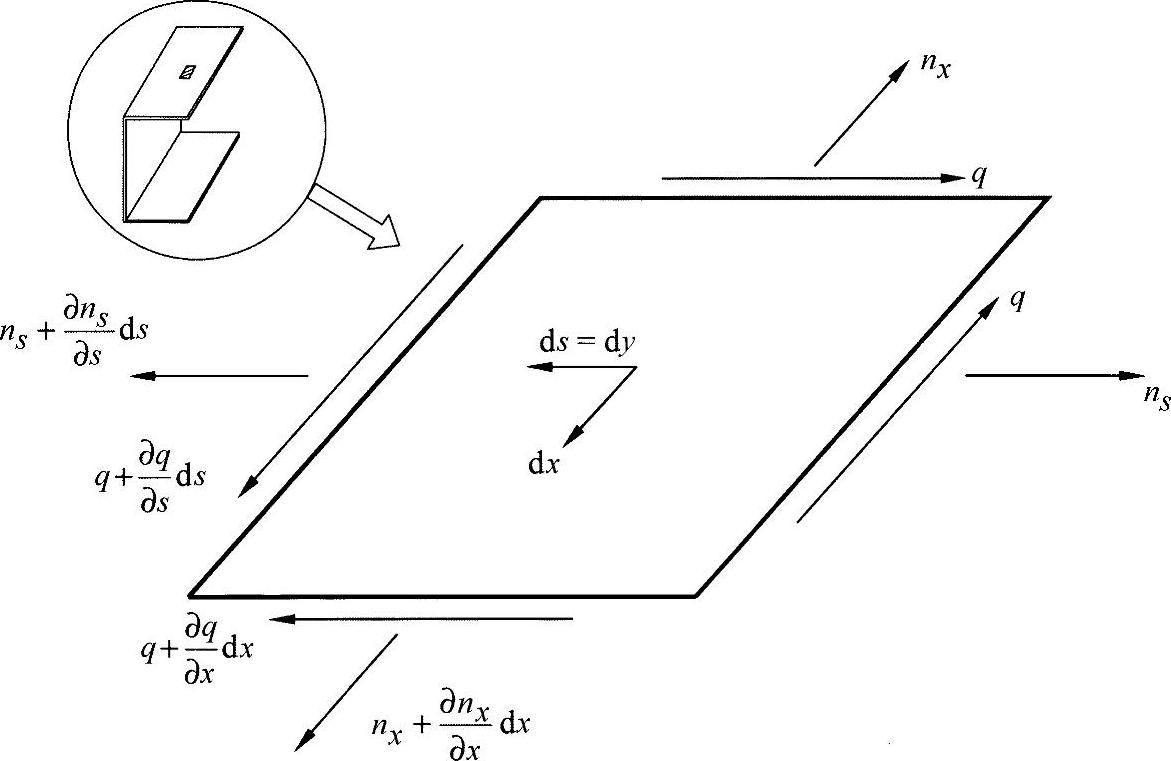
图9-3 带有倒角的型杆上的平面表层单元

由平衡得出：

这两个方程可标识为盘方程。它们描述了在平面板材上的应力载荷（亦见8.6.1小节）。根据前面所得出的结果可以看出，如果只考虑平衡，则无法确定三个未知量（n_x、n_s、q），因此，还需要列出特殊的边界条件。