轻量化设计：计算基础与构件结构中的板单元变形分析

板多作为型梁或者表层域（如：机翼蒙皮）的主要单元出现。与盘所受的力相比，在板单元中只有垂直作用于中心平面的外力。可根据图8-15中所示的平衡，将载荷与应力载荷联系起来。这里基于基尔霍夫板理论假设，该理论实际上由小变形条件与横截面保持水平的条件而得出。

研究力的作用可有：

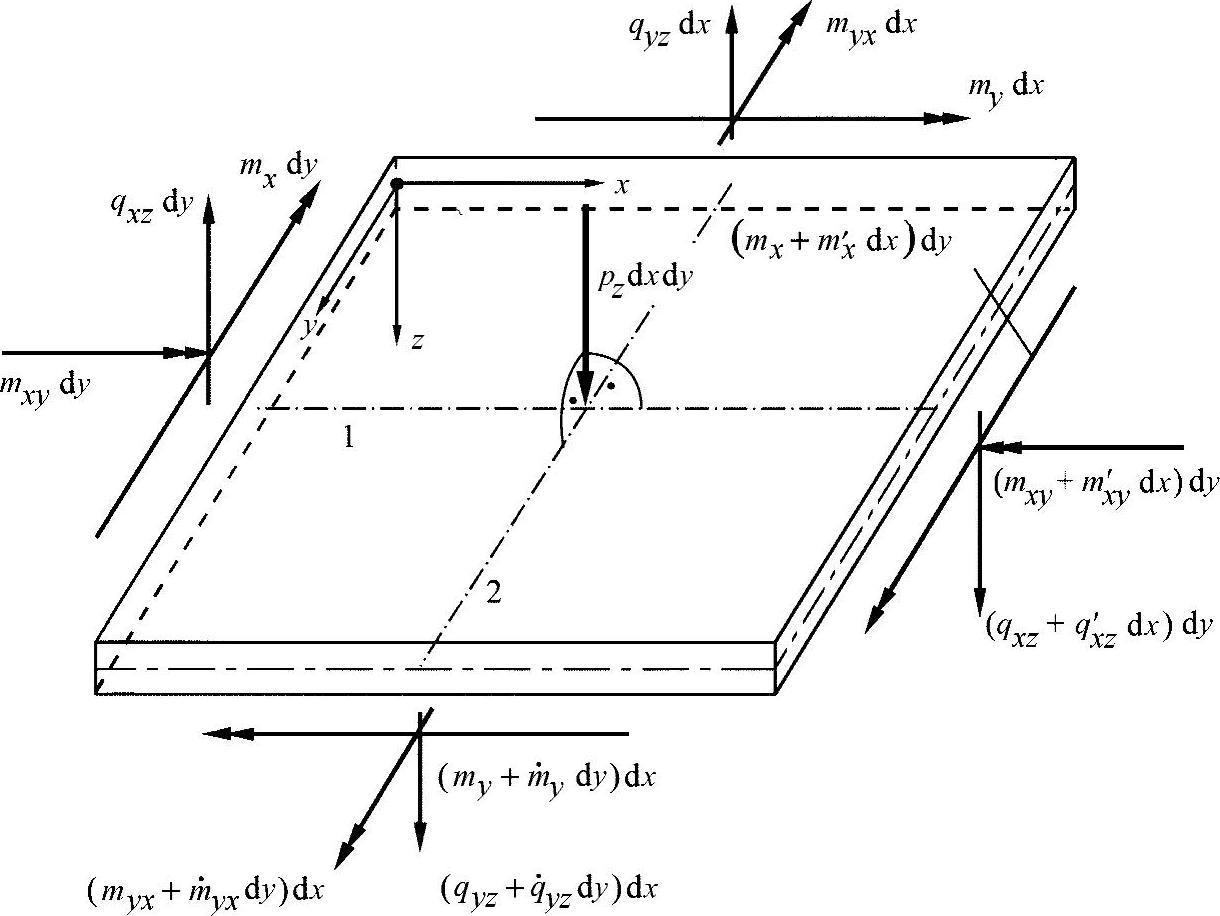
图8-15 板单元的平衡

●在z向的平衡

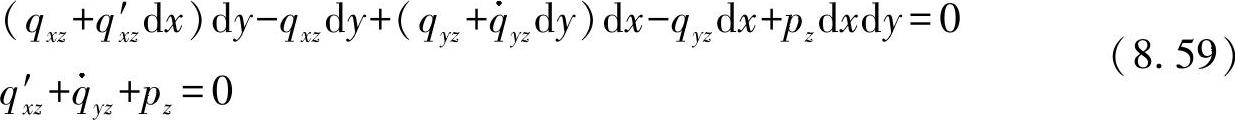
●围绕与x轴平行的重心轴1的力矩：

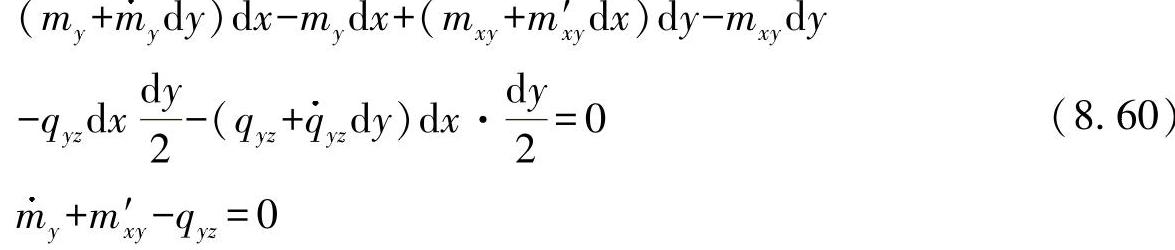
●围绕与y轴平行的重心轴2的力矩：

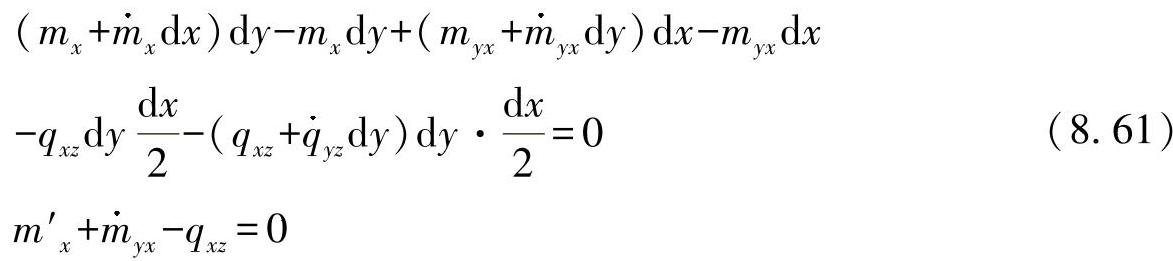
现在如果将方程式（8.60）与（8.61）代入方程式（8.59），可得出三个力矩的方程：

到此为止，当进一步的关系已知时，该含有三个未知量的方程可解。例如一个假设是基尔霍夫弯曲理论（横截面保持平面如伯努利），作为梁方程代入两个平面中。如图8-16所示，通过中心平面的挠曲w（x，y）可求出板单元的变形状态。

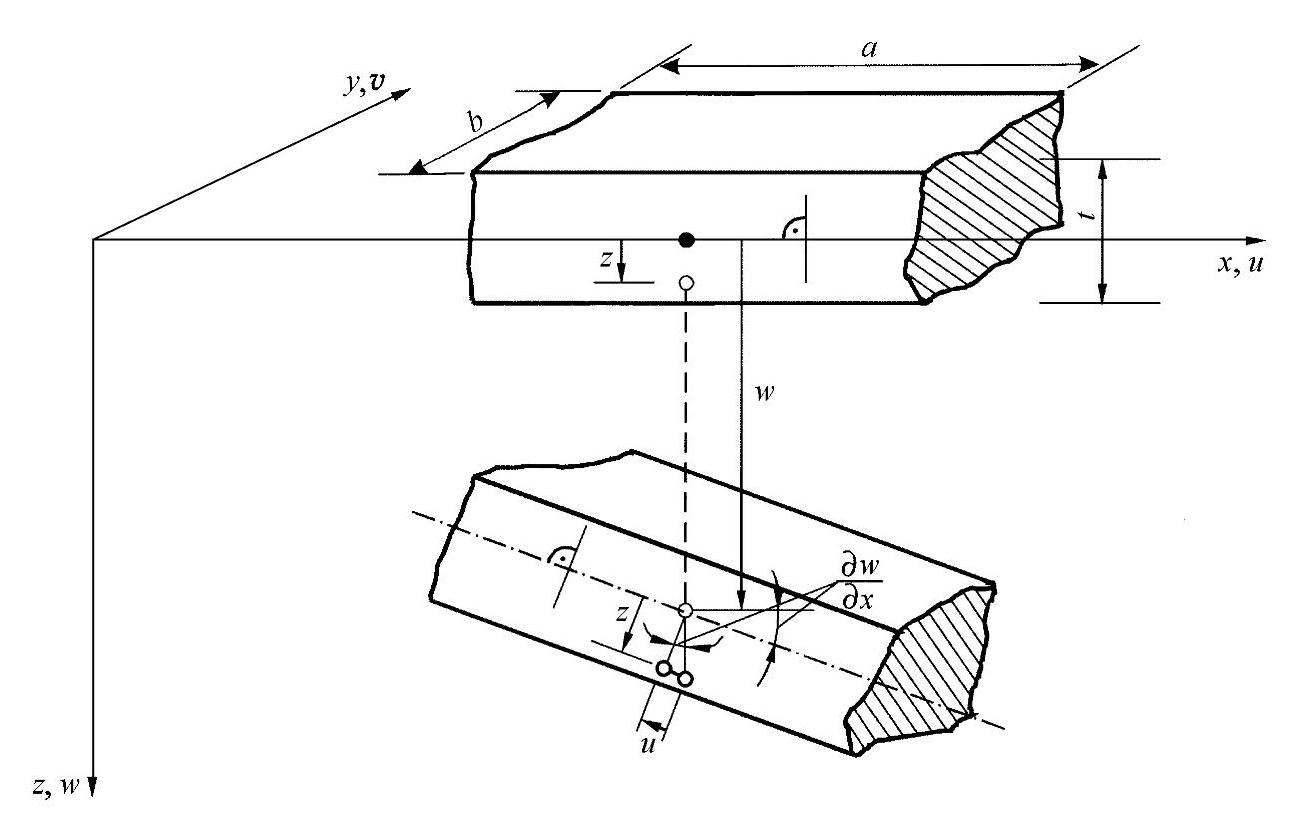
图8-16 在板或者模拟梁上的理想扭曲状态

由此得出所对应的位移为

相应的扭曲为

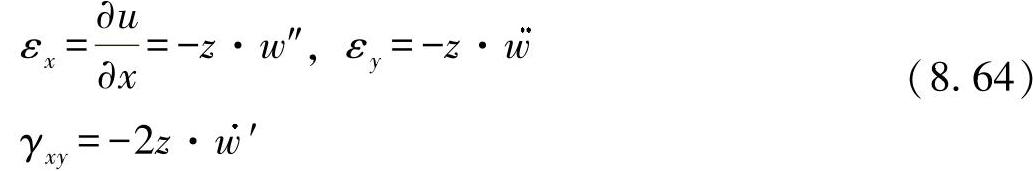
由此可得出针对平面应力状态[见方程（8.23）]的应力为：

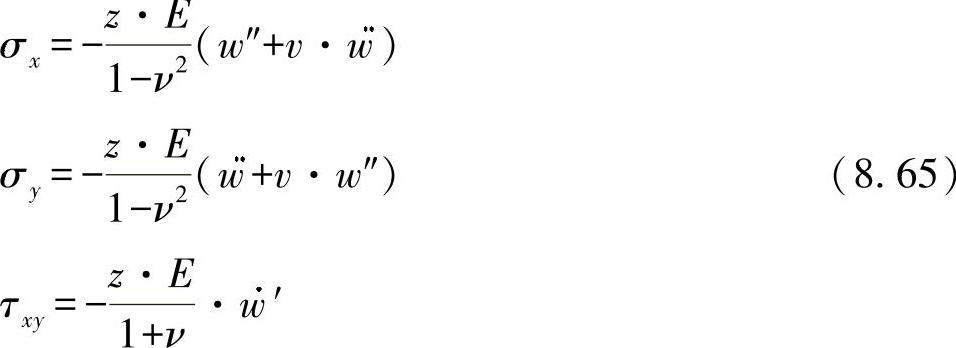
通过对应力之和的积分，可求出内力变量（采用长度单位定义）的内在关系。即有：

●对弯曲力矩

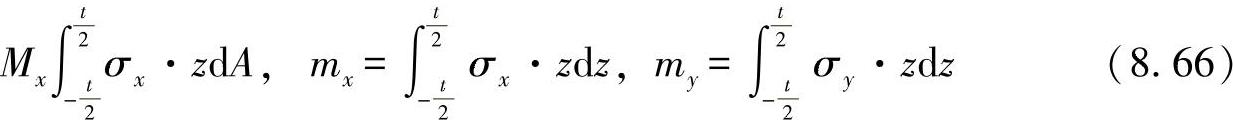
●对扭转力矩

●对横向力

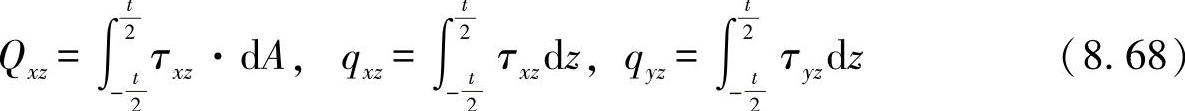
通过积分，可得出内力变量与挠曲的相关性，如：

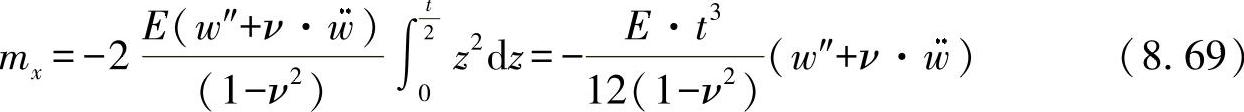(https://www.xing528.com)

求解上述方程，可得出力矩：

上式中，用：

引入板抗弯刚度。如果将这些值代入力矩微分方程（式8.62），可得出板方程（四阶不均匀微分方程）

在简单标准情形下，这些微分方程可根据Navier或者Lévy方法求解。当按Navier方法求解时，采用反对称级数计算挠曲和力分布，可得出：

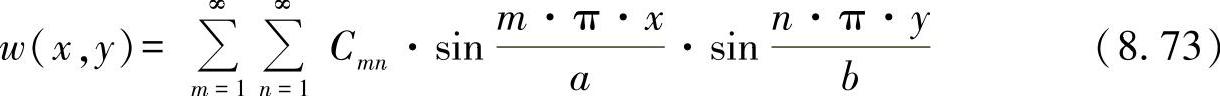
与

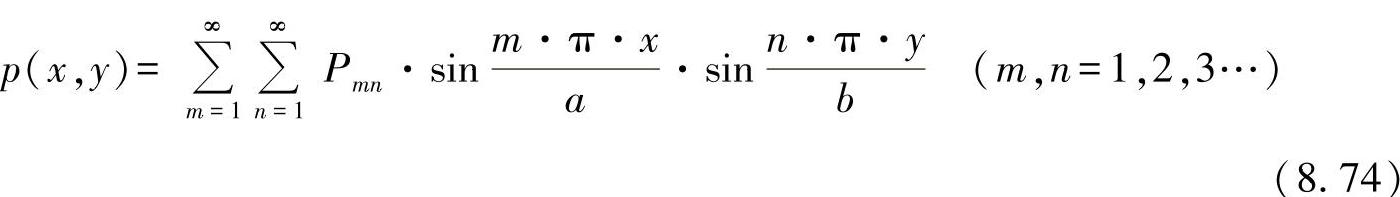
该解法适用于任意常数C_mn以及傅里叶系数：

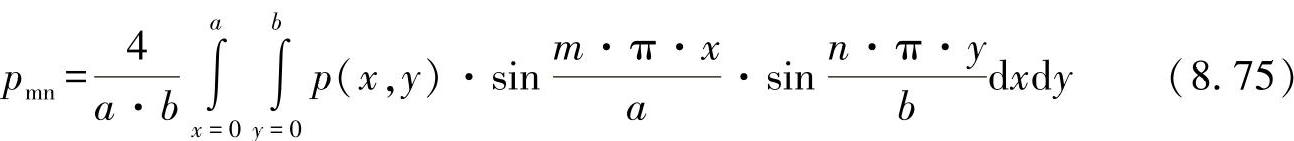
举例来说，对于在均匀分布载荷p（x，y）=p作用下自由平放的板，可借助傅里叶系数得出：

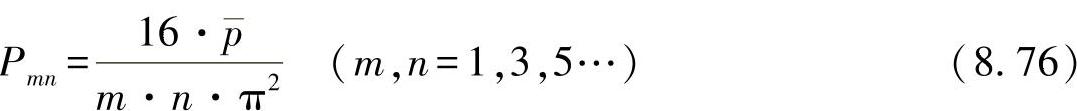
对于挠曲：

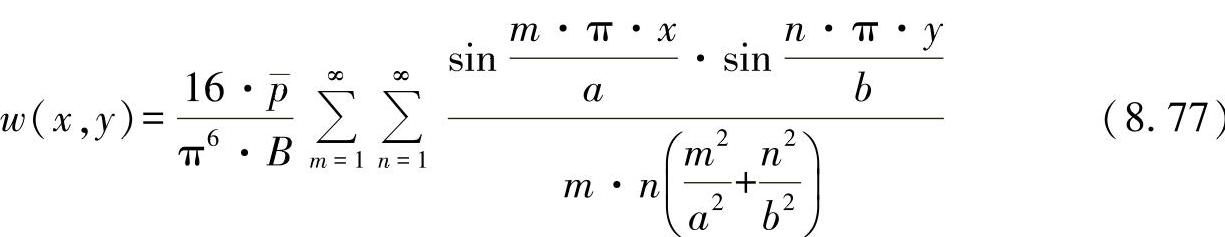
对于正方形的钢板（ν=0.3），最大挠曲发生在中心处：

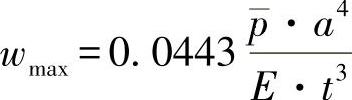
板中心的弯曲力矩为

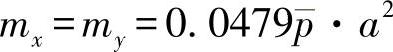
板上面的最大弯曲应力为

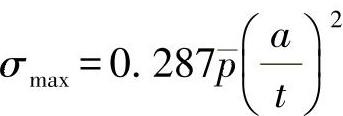
在点（x₀，y₀）导入一个单一载荷，则其对应的傅里叶系数为：

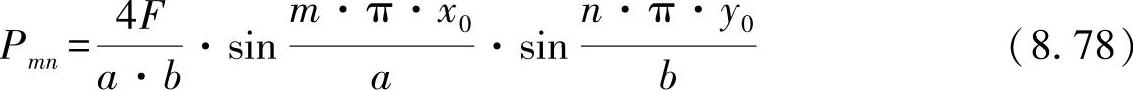
对于挠曲：

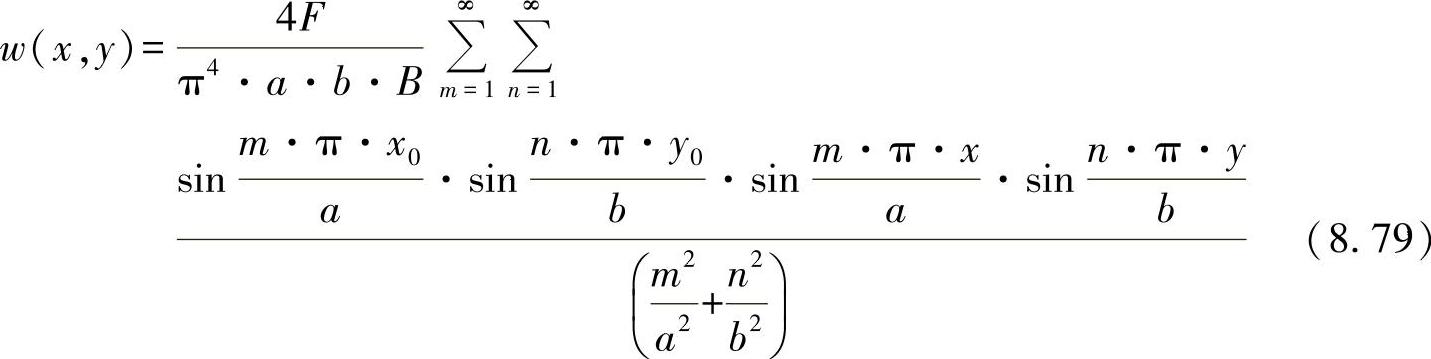
图8-17进一步列出了针对几个板问题的示范性求解。图中计算了板中心的挠曲以及在中心与边缘产生的应力。通过对比例关系的讨论，可清楚地看出，对于小的长宽比b/a<0.3，存在一个板带，实际上可用梁弯曲理论进行计算。

如上面所预计的，完全固定边界的挠曲与铰支产生的挠曲相比要小得多，但是在固定的板上（与在边缘上）所产生的应力与在铰支的板上所产生的应力相比，要明显高出许多。