轻量化设计：盘单元应力计算与载荷分析

盘单元作为构造单元的特征是：薄壁、外力只作用在单元的中心平面上。基于此，在单元内为平面应力状态，对于该状态可用8.3.4.1小节中的方程进行有效计算，图8-12描述了一个这样的盘单元。

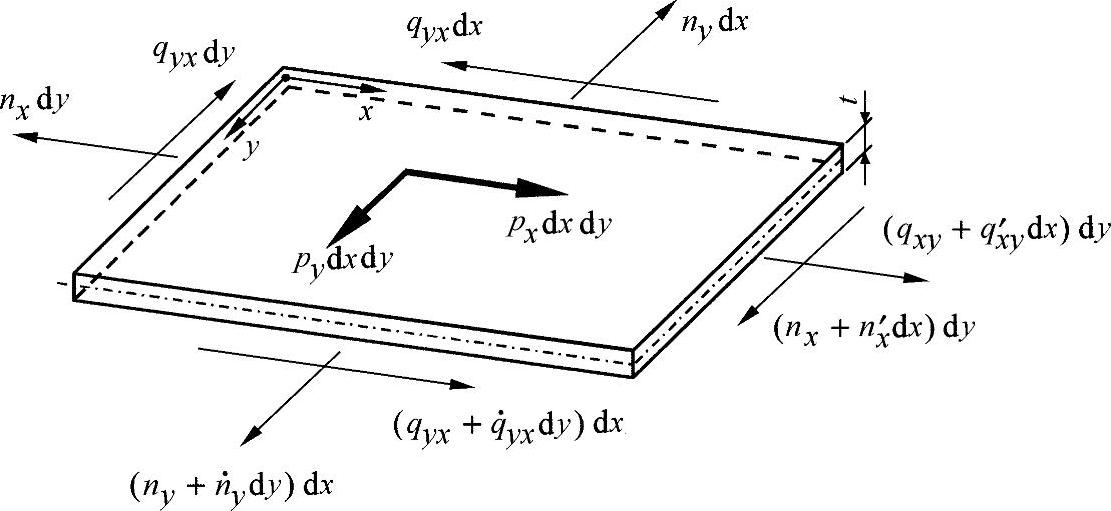
图8-12 薄壁盘单元上的载荷与应力载荷状况

这里最重要的是内力变量，可由在两个方向上的力平衡得出：

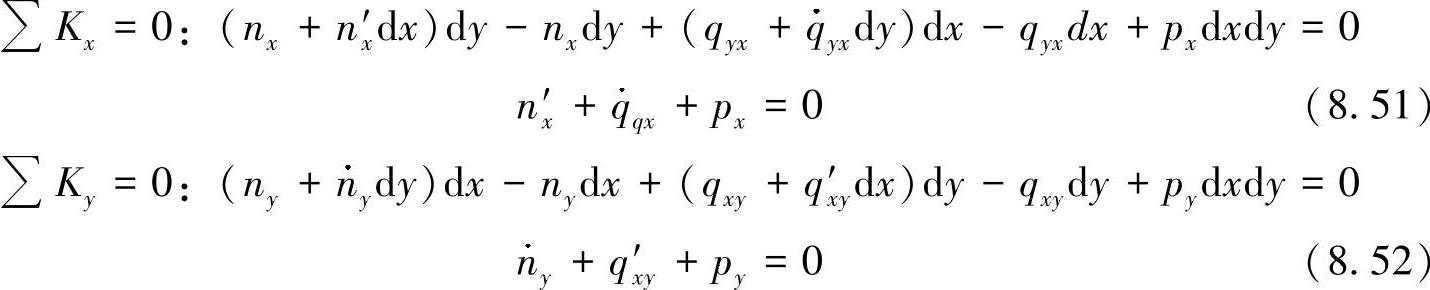
力矩方程可以进一步证明：q_xy=q_yx。通过以上得到的关系也证明了，在两个坐标方向上出现了彼此不相关的法向力，通过这些力可将剪力耦合在一起。另外也可以看出，这里导出的两个方程还不足以确定三个未知的内力变量n_x、n_y与q_xy。为了解决这个问题，需要提出盘方程。这里，初始关系为平面应力状态的相容性关系，由法向应变的二次微分并将其代入导出的方程可得出：

为求解应力，可引入一个应力函数（爱黎应力函数）F（x，y），特别满足相容性关系：

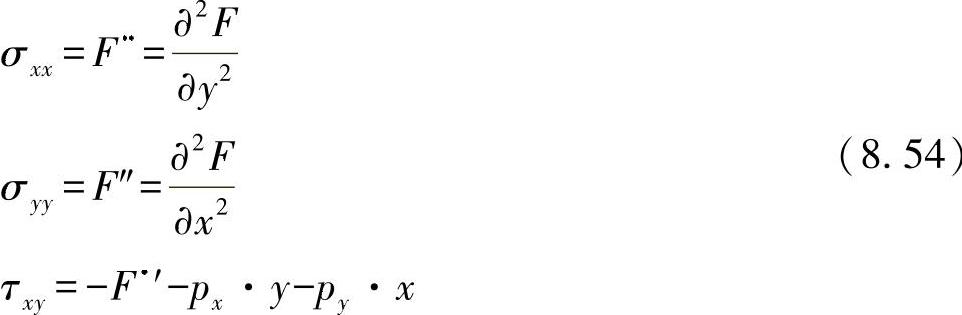
根据物质定律，可由方程式（8.53）得出进一步的关系，即：

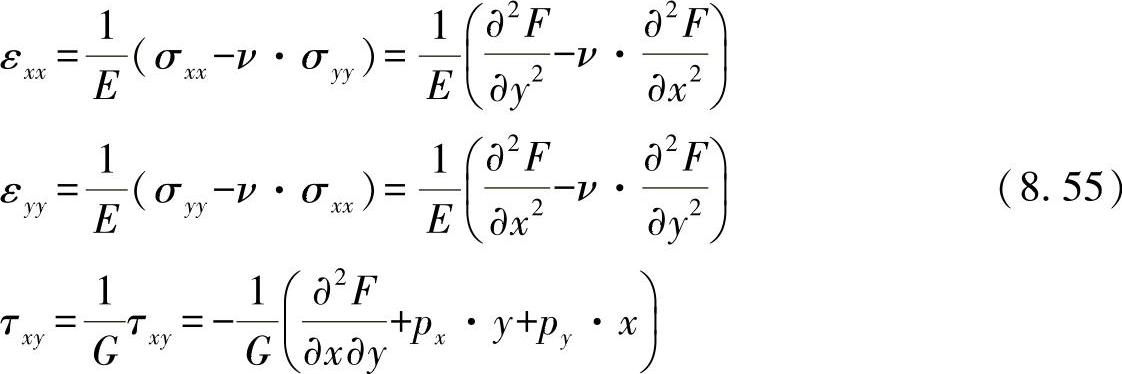
如果将在应力函数公式中的扭曲表达式代入相容性方程，则可得出：

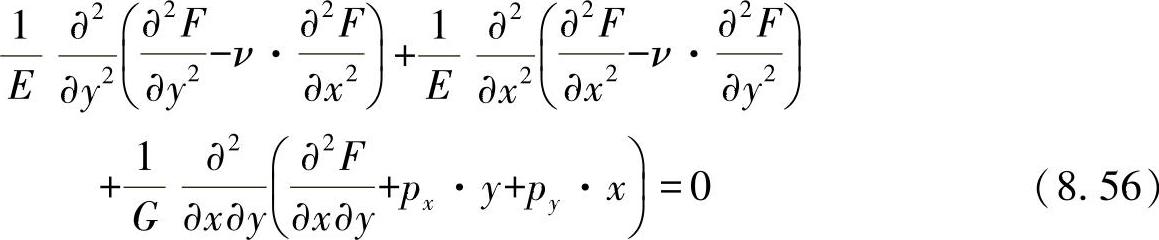
如果将其相乘，并根据已知的方式用弹性模量替代滑移模数，则可列出最终的方程：

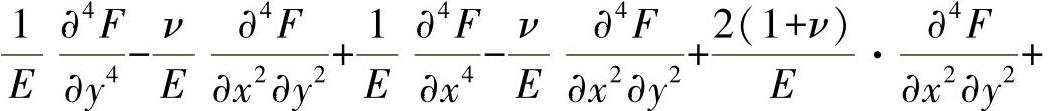
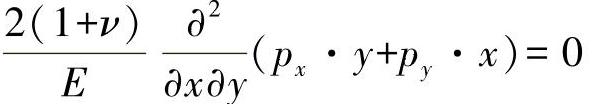
因此，可得出盘方程为

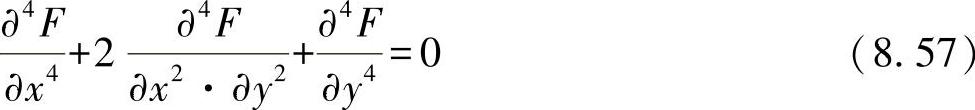
与

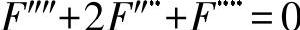
在考虑到边界条件下，这一部分四阶微分方程（双位方程）在列出特殊的解函数时，可用于近似地求解不同的盘问题。通常，如下简单的函数满足双位方程，如：

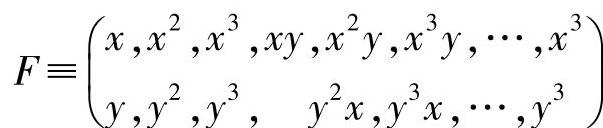
由方程式（8.54），可进一步确定应力并可通过以下方程：

n_x=σ_xx·t，n_y=σ_yy·t，q_xy=τ_xy·t （8.58）

确定边界上的内力变量。举例来说，在采用薄壁型材时，会经常遇到盘式构件与平面应力状态，如图8-13所示示例。

图8-14描述了典型的盘单元基本应力载荷状况。(https://www.xing528.com)

对于连续编号的普通应力载荷情形，可采用如下的解函数：

情形a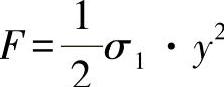：，其中：σ₁=常数

可满足ΔΔF=Δ⁴F=0^[1]

应力为

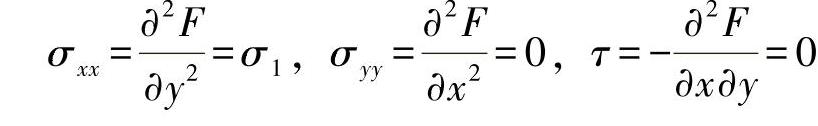
情形b：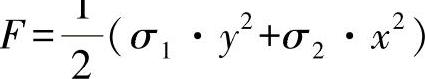

其中：σ₁，σ₂=常数

可满足ΔΔF=Δ⁴F=0

应力为

σ_xy=σ₁，σ_yy=σ₂，τ_xy=0

情形c：F=-τ·xy，τ=常数

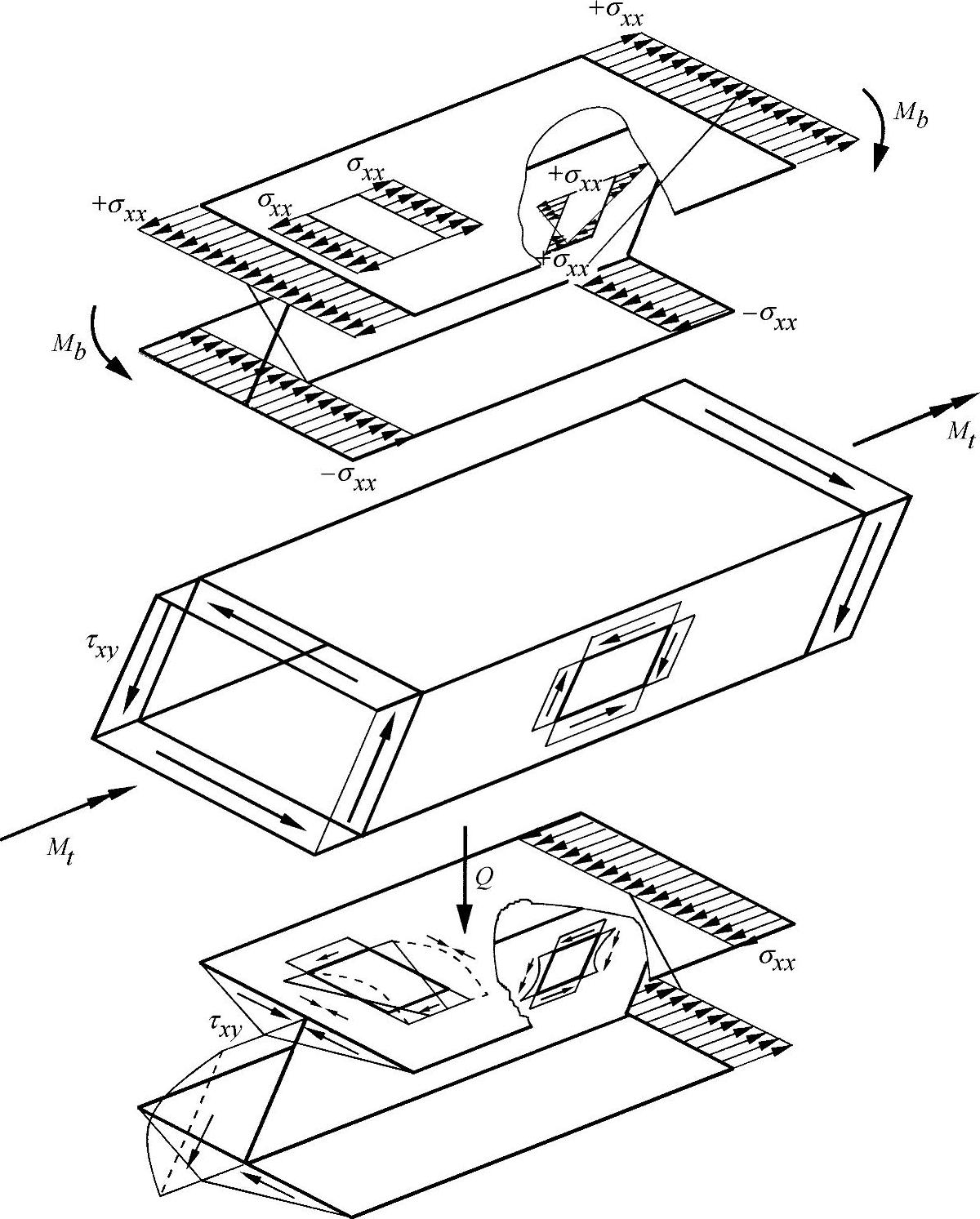
图8-13 型材单元的应力载荷状态[WIE 96a]

可满足：ΔΔF=Δ⁴F=0

应力为

σ_xx=0，σ_yy=0，τ_xy=τ

情形d：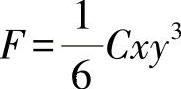

可满足：ΔΔF=Δ⁴F=0

应力为

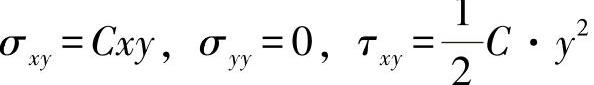
就是说，法向应力与高度呈线性关系，切应力则按高度的平方变化。

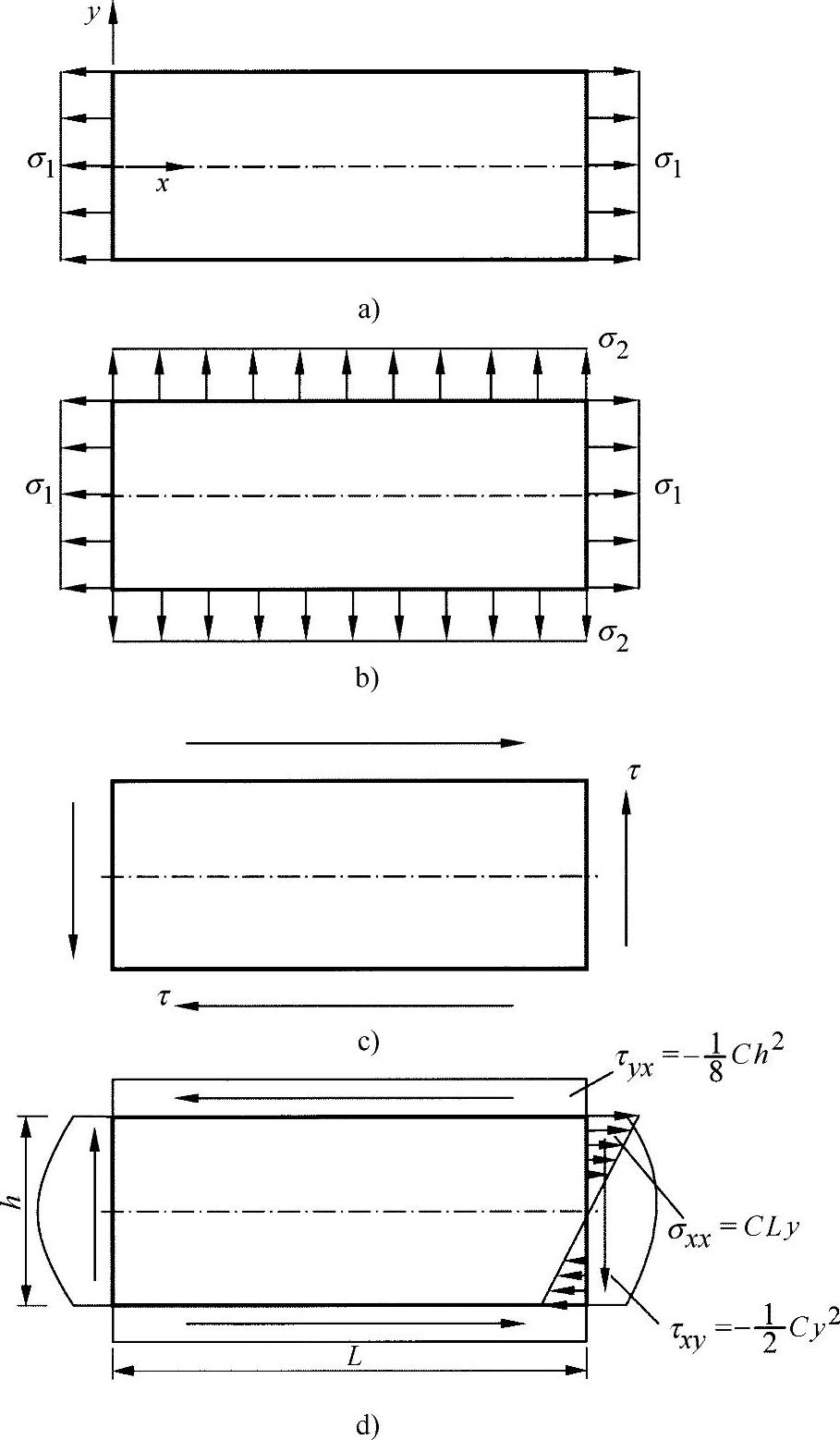
图8-14 盘单元上的基本应力载荷状况

a）单轴拉/压的盘 b）所有面拉/压的盘 c）纯剪切的盘 d）弯曲与剪切叠加的盘