载荷性能-确定材料弹性特征值的重要性

在混合设计、涂层连接或者纤维复合设计中，必须要特别谨慎地确定共同作用的材料的弹性特征值。图5-5所示为在单轴拉伸载荷作用下的单一方向的纤维复合材料。图中非常清晰地表明了材料所允许的载荷。按照经典的层压板理论（见VDI 2014），纤维和矩阵承担了完全不同的载荷：

●高使用率要求矩阵的延伸率大于纤维的延伸率：ε_BM≥ε_BF。

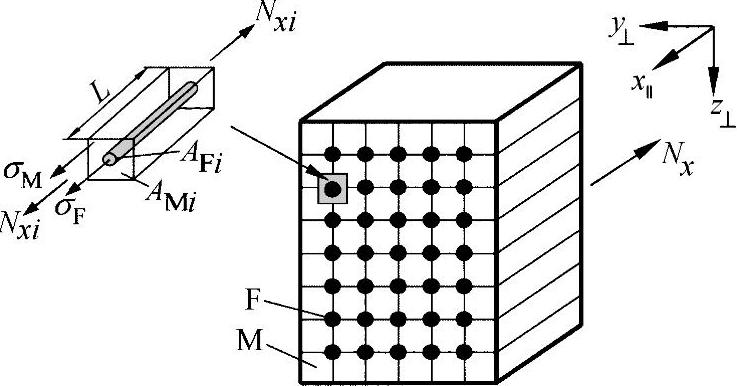
图5-5 纯法向应力载荷下的单一方向的层单元（UD-ES）

（F=纤维，M=基体，ϕ_F=纤维体积分量）

●通常来说，纤维的弹性模量远大于矩阵的弹性模量，即E_F>>E_M。借此，纤维将刚性层的载荷承接下来。

●即使在很小的变形下，纤维也存在断裂的危险。纤维断裂意味着层压板失效。

●通过层压板，纤维和基体按截面方向一为并联（‖），一为串联（⊥）。

在纤维方向上，由力平衡可得出：

σ‖·A=σ_F·A_F+σ_M·A_M （5.12）

考虑到几何条件：

ε‖=ε_F=ε_M=常数(www.xing528.com)

与线弹性物质定律：

σ_F=E_F·ε_F，σ_M=E_M·εM

可得出“混合规则”：

E‖·ε‖·A=（E_F·A_F+E_M·A_M）·ε‖

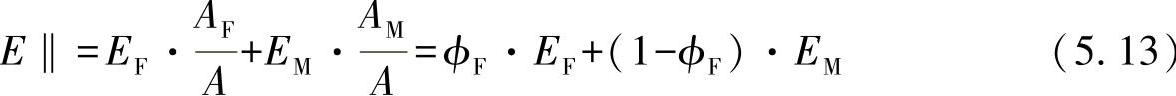
也就是说，实际上有一个由纤维和基体“混合”出来的弹性模量E‖=E_m在起作用。按[ÖRY 83]，纤维类复合的强度可由下式近似得出：

由此可得出承载比例：

从中可得出，材料的使用与纤维的体积成比例（约50%～55%）。