线弹性特征值：轻量化设计中重要的力学性能

首先需要考虑的是对构件设计非常重要的力学性能，特别是通过拉伸试验（DIN EN 10002-1）应力-应变图中得到的参数值。如图5-1所示，这些特征参数如下：

●按照胡克定律（Robert Kooke，1635—1703），至比例极限R_P，应力与可逆的弹性应变之间存在线性关系（ε_el～σ）。对于法向应力[MER 00]，胡克定律定义如下：

ε=β·σ （5.3）

式中，β为延伸系数。通常采用延伸系数的倒数值，即所谓的弹性模量E。则胡克定律可表示为

σ=E·ε

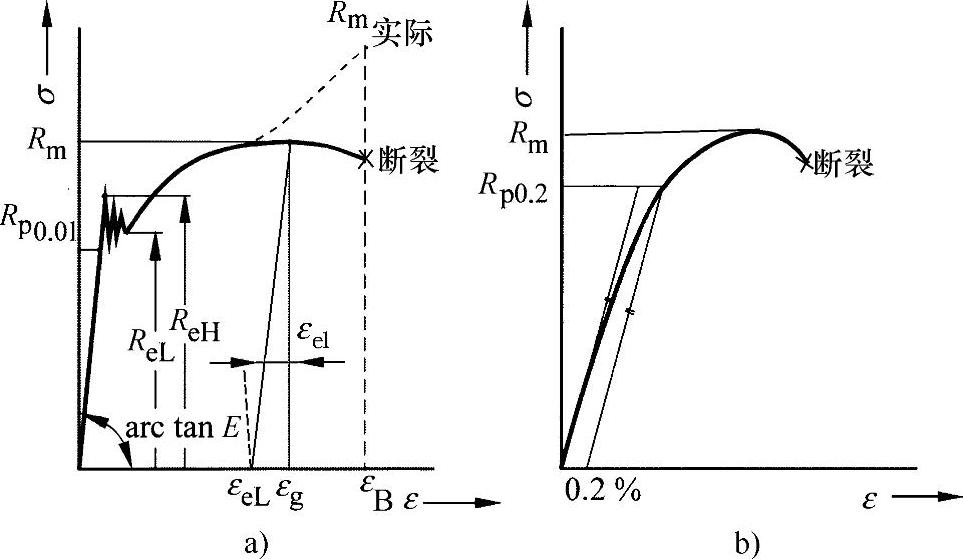
图5-1 根据拉伸试验得到的应力-应变图

a）软钢 b）高强铝合金

●从屈服强度R_eL、R_eH开始，材料开始显著流动。由于总的来说存在非线性材料行为，须用等效参数来表示，即定义弹性极限R_p0.01对应0.01%的参考应变或者屈服强度R_p0.2对应0.2%的参考应变。

●另外，抗拉强度R_m作为与试样初始横截面A_o相关的最大承受应力（高斯应力）也很重要，更重要的是实际承受的、使测试件局部开始断裂的应力R_m实际。假设体积不变（A_o·L_o=A·L），则皮奥拉-基尔霍夫应力为

σ_实际（ε）=σ（1+ε）

其中，实际应变为

ε_实际=ln（1+ε）

●按照定义，相关的伸长率（ε_实际，A）（%）(www.xing528.com)

为最大延长。由于给出的值取决于测量长度和横截面的比例关系，须由A（以前的A₅）或A_11.3（以前的A₁₀）进一步得出（参看DIN EN 10002-1）

L₀=（5～10）·d₀（圆形横截面）

有时候，以下的参数也有意义：

●用屈服强度比例R_eH/R_m表示材料的脆裂敏感性；

●切变模量G作为抵抗滑移的阻力指标，特别是对各向同性的材料，可借助弹性模量E^[1]通过下式联系起来：

●横向收缩率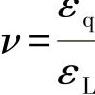（泊松数）表示与方向有关的材料体积变化。

在众多参数的确定中，与时间有关的参数值也很重要，如：

●材料的持久延伸极限σ_1/100000和持久断裂极限σ_B/100000，加载100000h后至1%的残余蠕变延伸或者发生断裂。

●在振动应力载荷下，任意长的允许应力振幅下的疲劳强度σ_A。

绝大多数情况下，这些特征值足以用来评估材料的使用了。在特殊情况下，还需要引入其他的评估参数，如对于裂纹断裂风险，需借助断裂韧性（K_c，K_Ic）进行评估。