计算方法：有限元方法和边界元方法在轻量化设计中的应用

正如开始所提到的，轻量化设计工作中相当的一部分时间是消耗在轻量化单元及其结构的设计上。稍后可以看到，这些工作主要是用来求解针对内力变量或者变形的微分方程或者方程组。出于教学的目的，在对接下来的几个子问题的数据处理上选择了分析求解方法，以便于清晰地说明设计的方法。不过，如今这个方法已经不再与实践完全吻合了。随着高性能计算机的普及，实际工作中已经越来越多地采用仿真计算方法。

在简单的弹性理论微分方程解法的最底层，可以导入微分方法或者傅里叶分析法。但是，在复杂的几何形状、多重载荷与实际边界条件同时出现时，这种方法常有其局限性。适用于此种情况的计算方法为有限元方法（FEM）或者边界元方法（BDM）[KLE 03]。

迄今为止，在这些纯数值方法中，有限元方法应用最为广泛也最为普及。有限元方法与边界元方法最主要的区别在于，有限元可以描述内部与边界，而边界元只能计算边界。关于两种方法工作原理的介绍超出了本章的内容，因此，这里只简单介绍有限元方法的几个基本要点。

有限元方法是面向计算的方法，借助力学单元（梁、盘、板、壳、块）的储存，提供用于软件技术的汇编算法与解析算法。

●有限元由其刚性矩阵标识，基于一定的变形假设条件（线形、正方形或立方形）；

●借助这些基本单元，建立起对应力学性能的结构，在结构中单元通过节点连接；

●在这个模型里进一步导入力并考虑到支承上的节点；(www.xing528.com)

●建立起一个大的线性方程组，通过计算程序求解该方程组；

●计算结果为节点的变形、应力与支承的反作用力。

该方法具有近似的特性，其原因在于所选择的变形方程、几何轮廓不保真趋近算法与算法的数字控制。尽管有这些局限，在绝大多数情况下，有限元方法比分析解法能更好地解决问题。为了证明这一点，见图3-2所示的一个简单例子，图中所示为模拟卫星运动的试验平台。试验采用的材料为不锈钢，在测试过程中模拟了卫星所受到的环境的影响（极冷与极热，温度变化范围-140～+100℃）。其动力学性能在准静态下测试，即在不同的位置通过等效力模拟实际应力载荷。这种模拟方法是完全可靠的，因为卫星在宇宙中的运动相对来说要慢得多。

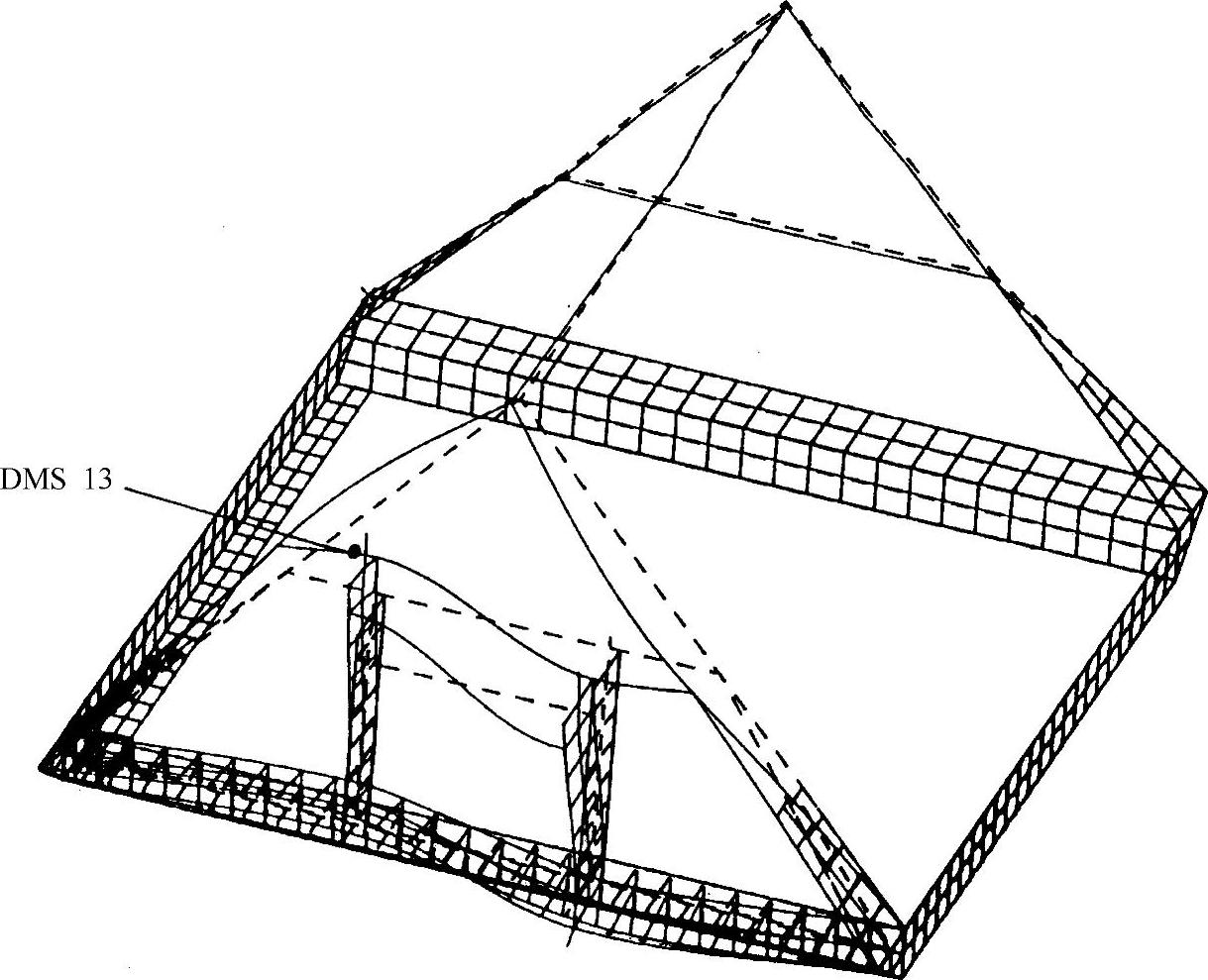
图3-2 源于有限梁单元与有限壳单元的试验模型

在修订设计参数后，试验平台得以建造并投入使用。通过试验可以对计算结果和测量结果进行比较。举例来说，图中标明的节点13处的计算应力为σ_理论=39.9MPa，DMS（应力计技术）测量结果为σ_实际=38MPa，误差为4.76%。这是一个非常小的偏差，其他情况下测量到的偏差最大为13%。