王绍武等人认为,全球气候模式的不确定性主要体现在三个方面,即经济的不预测性、模式的差异性和利用大气环流模式来驱动区域模式时的不确定性(王绍武等,2013)。其中,对于第二种不确定性而言,主要表现在各模式均有自己的特色,在某些方面都具有独特的优势,且不同模式的物理过程不同,因此,模式间的差异性可能会加大。本书的研究为了减少这种不确定性,以概率分布吻合最优为原则,对模式进行评价,并筛选出不同时段、不同区域的相对最优模式,用相对最优模式作为气象驱动,对滦河流域未来干旱灾害风险进行预估。
本书中用于评价气候模式的实测数据选用的是中国地面降水日值0.5°×0.5°格点数据集(V2.0)和中国地面气温日值0.5°×0.5°格点数据集(V2.0)(http://cdc.cma.gov.cn/),数据时段为1961年1月1日至2012年7月31日,数据空间分辨率与ISI-MIP提供的5套全球气候模式一致,均为0.5°×0.5°。该套数据集是以全国国家级台站日降水量/气温观测数据为基础,利用薄盘样条法(Hutchinson,1998a;1998b)进行插值,同时引入数字高程资料以尽可能地消除中国区域独特地形条件下高程对空间插值精度的影响。其中,用于插值的气象数据是全国2474个国家级台站近50年逐日降水量和气温资料,地形数据是由GTOPO30数据(分辨率为0.05°×0.05°)经过重采样生成的中国陆地0.5°×0.5°的数字高程模型DEM。数据集评估结果表明,格点分析值与观测值误差较小。具体的插值方法和数据评价结果可参见《中国地面降水0.5°×0.5°格点数据集(V2.0)评估报告》(赵煜飞,2012)和《中国地面气温0.5°×0.5°格点数据集(V2.0)评估报告》(沈艳,2012)。用于评价模式的格点分布如图6.4所示,滦河流域内部及周边共计46个格点。
图6.4 研究选取格点空间分布
利用1961年1月至2000年12月期间的实测和模拟的逐月降水/气温数据,依据“概率分布吻合最优”为原则,对气候模式的适用性进行评价,具体方法如下:
(1)选取合适的分布函数对实测和模拟的月降水/气温数据进行拟合,其中,鉴于零降水月数的影响,月降水选用阶跃函数和2参数伽马分布函数组成的混合函数进行拟合[式(6.1)],月气温选用4参数的贝塔分布[式(6.3)](陶辉等,2013)。
1)混合函数:
![]()
式中:p为有降水的月占全部月系列的比例;H(x)为阶跃函数,当降水量大于0时取1,当降水量等于0时取0;F(x)为2参数伽马分布函数,其概率密度函数为
![]()
2)贝塔函数概率密度:
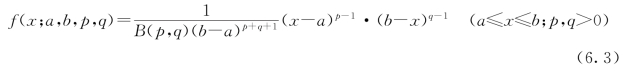
(2)定义一个评分值Skill Score(以下简称SS值),用以定量化气候模式对降水和气温的模拟效果。SS值的大小即为月降水或气温的实测值和模拟值概率密度曲线所围成的公共部分面积,如图6.5所示。SS的值介于0和1之间,当SS=0时,说明实测值和模拟值的概率曲线完全没有重合部分,而当SS=1时,说明实测值和模拟值的概率曲线完全重合,因此,研究认为,SS值越大,模式模拟效果越优。(https://www.xing528.com)
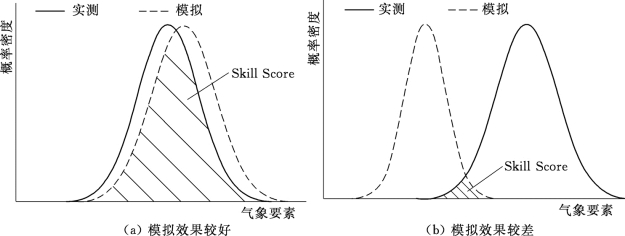
图6.5 模式评价方法示意图
以坐标为(118.75°E,40.25°N)的典型格点7月份降水数据为例(见图6.6),对上述方法的具体过程进行介绍。图6.7为该典型格点7月份降水实测值和模拟值概率密度曲线对比情况,按照图6.5中对SS的定义,可得到GFDL-ESM2M、Had GEM2-ES、IPSL-CM5A-LR、MIROC-ESMCHEM和Nor ESM1-M的SS值分别为0.96、0.70、0.87、0.91和0.80,因此可认为,对于该格点7月份降水量的模拟而言,GFDL-ESM2M为相对最优模式。
采用上述方法可评价各格点对于某一月份降水模拟效果,据此可以筛选出各格点在指定月份降水模拟的相对最优模式。图6.8为7月份降水模拟相对最优模式空间分布情况,从图中可以看出,对于滦河流域7月份降水模拟而言,大部分地区的相对最优模式为GFDL-ESM2M,主要分布在滦河流域中下游地区。同理,可得到其他月份降水和气温模拟的相对最优模式空间分布情况。
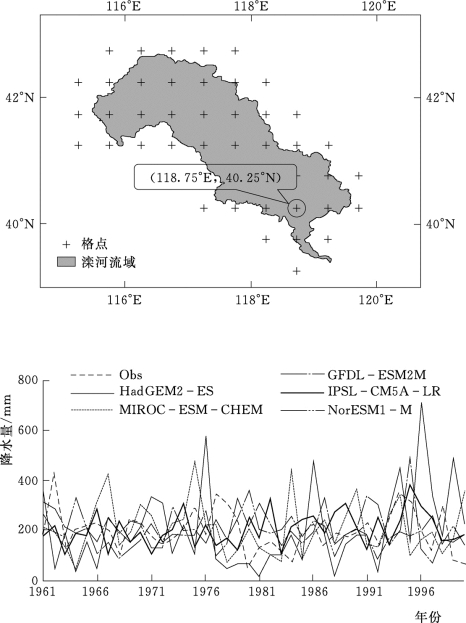
图6.6 典型格点空间位置及其7月份降水年际变化过程
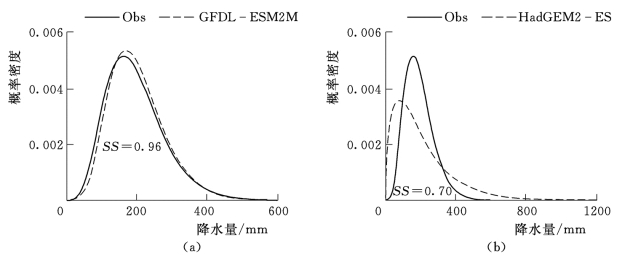
图6.7(一) 典型格点7月份降水量模拟值和实测值概率密度曲线
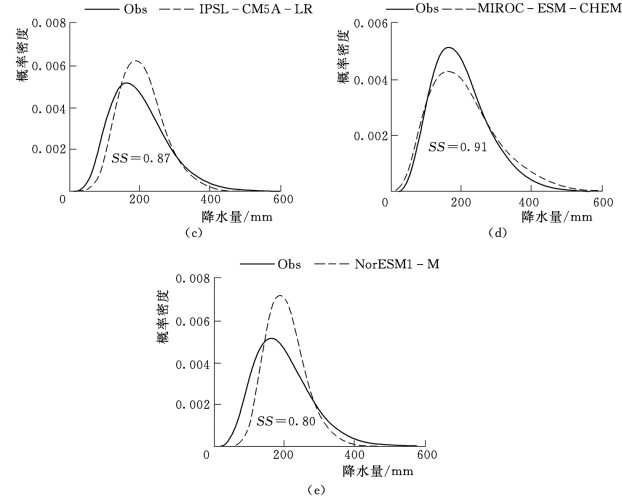
图6.7(二) 典型格点7月份降水量模拟值和实测值概率密度曲线
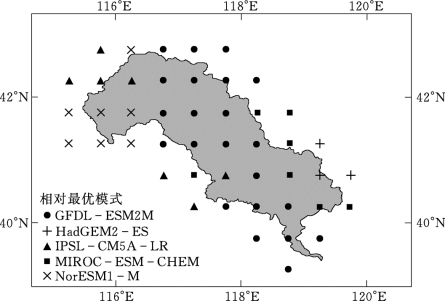
图6.8 降水模拟相对最优模式空间分布(7月)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




