变化环境下干旱风险评价与综合应对

（1）滦河流域各单元逐月供水量和需水量计算。根据第2章的理论框架，滦河流域干旱评价中的供水量（WS）可认为是降水形成的地表水和地下水（W）与实际蒸发（Ee）之和，即

其中，W可认为是每个水文响应单元的地表径流（Rsurf）、壤中流（侧流）（Rlat）、地下径流（Rgw）三部分之和，因此，WS的计算公式可写为：

上述参数均可由SWAT模型输出分项提供。

滦河需水量（WD）可认为是耕地、林草地、城镇和建设用地需水量之和，相关用水分项已在第4章4.5～4.7节予以计算得到。

（2）滦河流域干旱指数演算公式。在获取各评价单元逐月供水量和需水量后，可得到各单元逐月水资源短缺量（d）：

参照PDSI干旱指数的思想，根据水资源短缺量可以求得各月水资源短缺指数（z）：

式中：k*为未经过修正的水资源短缺修正系数，反映水资源短缺的时空差异性，可根据以下公式计算得到：

式中：k*为某一评价单元在某一月份的水资源短缺修正系数；分别为某一评价单元在某一月份的多年平均需水量和供水量。

但按式（5.5）计算得到的z值仅表示当月水资源短缺的情况，无法反映在此之前的1个月或者是数个月的累积影响，因此，需引入表征水资源短缺量和持续时间的函数关系式（许继军等，2010）。因此，本书的研究在统计滦河流域88个评价单元不同干旱持续时间（此处取1～12个月）与累积z值（∑z），取各持续时段最小的∑z，假定其为不同持续时间的极端干旱，令x=-4.0作图，并将纵坐标分成四等份，绘制出另外3条直线，分别表示严重干旱（x=-3.0）、中等干旱（x=-2.0）和轻微干旱（x=-1.0）（图5.2）。根据图5.2可以确定干旱指数（x）与水资源短缺指数累积值（∑z）和持续时间（t）三者间的函数关系，即

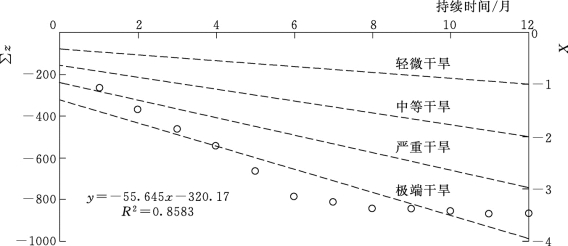
图5.2　干旱等级与水资源短缺累积量和持续时间的关系

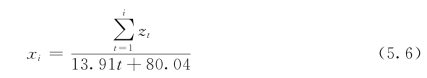
（3）滦河流域干旱指数累积关系的递推公式。由于前一时段的∑z会对后一时段的z值造成影响，例如，如果某两个月的z值相同，但其中一个出现在几个较湿润的月之后，而另一个出现在几个较干旱月之后，理论上来看，后者的干旱程度应该高于前者，因此，需进一步确定每个月的z值对x值的影响（刘巍巍等，2004）。令i=1，t=1，式（5.6）则可写为：

(www.xing528.com)

假设本月是干旱的开始，则：

如果要维持上一个月的旱情，随着时间（t）的增加，累积的水资源短缺指数（-∑z）也应该随之增加。但t值的增加是恒定的（每月增加1），因此，要维持上一个月的干旱指数，所需要增加（-z）值取决于前一时段的干旱指数，故令

令t=2，xi=xi-1=-1，由式（5.6）和式（5.8）可得C=-0.15，则式（5.9）可写为：

（4）权重因子修正。式（5.4）中的k*仅受月需水量和月供水量平均值的影响，但实际上水资源短缺修正系数还受水资源短缺量的影响（与其绝对值的平均值成反比）。因此还需对其进一步修正。假设一年中每一个月均为极端干旱（x1=x2=…=x12=-4），则代入式（5.6）可得∑z=-987.9。这12个月对于任何一个评价单元而言，都可认为是极端干旱，则如若得知各评价单元最旱的12个月所对应的水资源短缺总和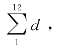则该评价单元的极端干旱平均权重可按如下公式进行计算：

计算各评价单元月_平均供水量需水量和缺水量和极端干旱平均权重可得如下回归方程（见图5.3）：

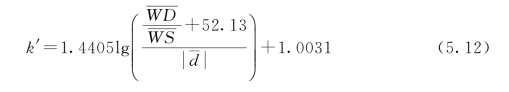
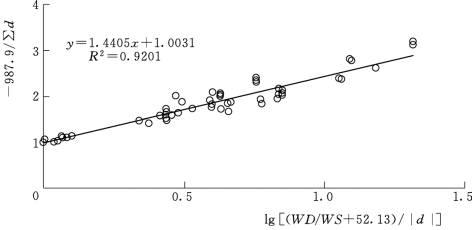
图5.3　修正系数k的近似拟合

按照式（5.12）可计算得到88个评价单元的平均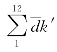值为296.8，对k′进一步修正，得各评价单元的修正系数k，如式（5.13）所示：

根据式（5.12）、式（5.13）和式（5.4）可求得各评价单元逐月修正后的水资源短缺指数zi，再将zi带入式（5.10）可评价各单元干湿等级。干旱等级划分仍采用PDSI的等级划分标准，如表5.1所列。

表5.1　干湿等级划分标准