本节主要介绍等精度观测和不等精度观测的精度评定方法。要求学生通过精度评定相关内容的学习，能够根据实际观测数据，正确评定观测值的精度。
6.4.1 等精度观测的精度评定
1.算术平均值的中误差
设在等精度的观测条件下，对某未知量进行n次观测，观测值分别为l1，l2，…，ln，相应各观测值的中误差为ml1，ml2，…，ml n。
据算术平均值的函数式 x＝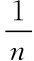
（l1＋l2＋…＋ln）
由式（6－11）推得算术平均值的中误差为：
因各次观测值都是等精度观测，即ml1＝ml2＝…＝ml n＝m，则：
结论：算术平均值的中误差等于观测值中误差的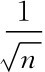
倍。
例6.10 设对某水平角施测了5个测回，若一测回的测角中误差m＝±20″，试求5个测回的水平角平均值的中误差mβ。
解：由式（6－20）得：
2.观测值中误差
观测值的精度是以中误差来衡量的。当观测值的真值已知时，每个观测量的真误差Δ可以求出，根据公式（6－3）可计算出中误差m。但在一般情况下，观测值的真值往往无法获得，因此实际上不能用真误差来计算中误差。然而由于算术平均值是真值的最或是值，算术平均值可根据观测值计算得到，所以在平差计算时可利用观测值的算术平均值代替真值，通过计算观测值的改正数来进行平差计算。
（1）观测值的改正数。
观测值的改正数是观测值的算术平均值x与观测值li之差，用vi表示，即：vi＝x－li。
v1＝x－l1
v2＝x－l2
……
vn＝x－ln
将上列等式相加，得：
由上式可知，观测值的改正数之和恒等于零，可以用作计算中的检核。
（2）观测值中误差计算。
设在等精度的观测条件下，对某未知量进行n次观测，其观测值分别为l1，l2，…， ln，该量的真值为X，算术平均值为x，观测值的改正数分别为v1，v2，…，vn，相应的真误差为Δ1，Δ2，…，Δn，则
Δi＝li－X （i＝1，2，…，n）
vi＝x－li（i＝1，2，…，n）
将上列两等式相加，得：
Δi＝（x－X）－vi（i＝1，2，…，n）
将上式两边平方求和，并除以n，得：
由式（6－21）可知：［v］＝0
（x－X）是最或是值（算术平均值）的真误差，难以求得，通常以算术平均值的中误差mx代替。将算术平均值x的中误差mx＝±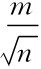
代入（6－22）式得观测值的中误差为：
将（6－23）式代入mx＝±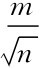
中，得用观测值的改正数计算算术平均值中误差公式为：
例6.11 设丈量A、B两点间距离，丈量6次的结果如表6.2所示，求观测值的中误差及算术平均值的中误差。
表6.2 A、B两点间距离丈量结果
观测值的中误差为：
算术平均值的中误差为：
距离： DAB＝133.647m±0.0023m
6.4.2 不等精度观测的精度评定
1.加权算术平均值（最或是值）的中误差
设对某一未知量进行了n次非等精度的观测，观测值分别为l1，l2，…，ln，相应各观测值的权为p1，p2，…，pn，相应各观测值的中误差为m1，m2，…，mn。
将公式展开为：
根据误差传播定律，加权算术平均值的中误差为：(www.xing528.com)
根据单位权的定义公式（6－18），可得：
将各mi代入上式得：
式中：M为加权算术平均值中误差；
u为单位权中误差；
［p］为各观测值的权之和。
2.单位权中误差
在（6－25）式中，要计算加权平均值的中误差时，必须先求出单位权中误差u。
（1）根据真误差计算单位权中误差。
由单位权的定义式可知：
u2＝p1m21
u2＝p2m22
……
u2＝pnm2n
将上述等式两边相加得：
nu2＝p1m21＋p2m22＋…＋pnm2n＝［pmm］
则：
当n→∞时，用真误差Δ代替中误差m，衡量精度的意义不变，则可将上式改写为用真误差计算单位权观测值中误差的公式：
将（6－26）式代入（6－25）式中得加权算术平均值的中误差为：
（2）根据最或是误差计算单位权中误差。
在多数情况下，真误差是不能求得的，所以要用最或是误差vi来计算单位权中误差。在非等精度观测中，观测值的最或是误差为观测值li与观测值的加权算术平均值x0之差，用vi表示，即：vi＝li－x0。
最或是误差为：
v1＝l1－x0权p1
v2＝l2－x0权p2
……
vn＝ln－x0权pn
将上述等式两边乘以相应的权得：
p1v1＝p1l1－p1x0
p2v2＝p2l2－p2x0
……
pnvn＝pnln－pnx0
将上述等式两边相加得： ［pv］＝［pl］－［p］x0
将x0＝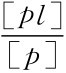
代入上式得：
［pv］＝0
由上式可知，观测值的加权改正数之和恒等于零，可以用作计算中的检核。
类似公式（6－26）的推导，可以求得用最或是误差来计算单位权中误差的公式为：
加权平均值中误差为：
式中：
vi＝x0－li
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
