测绘基础：平差值计算成果

本节主要介绍测量平差、最或是值的概念及等精度观测和不等精度观测平差值的计算。要求学生通过测量平差值计算相关内容的学习，能够根据实际观测数据，正确计算未知量的最或是值。

自然界中任何一个独立未知量（如某一个角度、某一段长度等）的真值都是无法得知的，只有通过多次重复观测，才能对其真值做出可靠的估计。然而，由于有了多余的观测，观测值之间就会存在矛盾。因此，除了要对观测值的精度做出评定外，还要依据各观测值求未知量最可靠的估值，这项工作称为测量平差，简称平差。未知量最可靠的估值应是一个最接近该量真值的值，称为最或是值。

对一个未知量观测值进行的平差，称为直接观测平差，它分为等精度直接观测平差和不等精度直接观测平差。在相同条件下对某量进行n次观测，通过数据处理，求出被观测值真值的最或是值（即最可靠值），同时评定该最或是值的精度，称为等精度直接观测平差。在不同条件下对某量进行n次观测，通过数据处理，求出被观测值真值的最或是值，同时评定该最或是值的精度，称为不等精度直接观测平差。

6.3.1 等精度观测平差值计算

在实际工作中，我们常常对一组等精度观测值，取其算术平均值作为该量的最或是值。

设在等精度观测条件下，对某未知量进行n次观测，观测值分别为l1，l2，…，ln，算术平均值为

式中：n为观测次数；

l1，l2，…，ln为各独立观测值。

下面证明在等精度观测条件下，各观测值的算术平均值x是最接近真值X的值，即该未知量的最或是值。

设某未知量的真值为X，观测值分别为l1，l2，…，ln，各观测值的真误差分别为Δ1，Δ2，…，Δn，则：

Δ1＝l1－X

Δ2＝l2－X

……

Δn＝ln－X

将上列等式相加并除以n，得：

根据偶然误差抵消性的性质即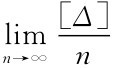＝0得：

当观测次数n无限增大时，观测值的算术平均值趋近于该量的真值。但由于在实际工作中不可能对某量进行无限次的观测，故算术平均值不等于真值，但可认为算术平均值是根据已有的观测数据，所能求得的最接近真值的值，视为最可靠值，即未知量的最或是值。

6.3.2 不等精度观测平差值计算

1.权的概念

在实际测量中，除了等精度观测外，还有不等精度观测。如图6.3所示为一组不等精度观测的观测结果，当进行水准测量时，由高级水准点BMA、BMB分别通过不同的水准路线测至节点E，测得E点的高程为H′E、H″E。在这种情况下，即使观测中所使用的仪器和方法均相同，但由于水准路线的长度不同，因而测得E点的两个高程观测值的可靠程度也不相同。

图6.3 不等精度观测

设两条水准路线的高差分别为h1、h2，相应路线的测站数为n1＝9、n2＝4，各测站中误差相等均为m，则两条水准路线的中误差分别为：

AE路线的中误差 m1＝m＝3m

BE路线的中误差 m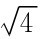2＝m＝2m

由上式可看出，由于AE路线比BE路线的测站数多，故中误差m1＞m2。在计算观测值的最或是值时，不能简单地取两个高程观测值的算术平均值作为最或是值，应考虑到各观测值的质量和可靠程度。精度较高的观测值h2应给予较多的信赖，在计算最或是值时应占较大的比重，精度较低的h1应占较小的比重。

各不等精度观测值的可靠程度，可用一个数值来表示，称为各观测值的权。通常用P表示。“权”是权衡轻重的意思，观测值的精度愈高，其权愈大。

设在不等精度观测条件下，对某未知量进行n次观测，观测值分别为l1，l2，…，ln， p1，p2，…，pn表示各观测值的权，m1，m2，…，mn表示各观测值的中误差。在测量学中，权的定义公式为：

式中μ为任意选定的常数，但在用上式确定一组观测值的权时，μ只能选用一个定值。由此可见，权是与中误差平方成反比的一组比例数。即：

或 　p1m21＝p2m22＝…＝pnm2n＝μ2 　（6－17）

上例中若以p1、p2分别表示AE路线与BE路线观测结果的权，并令μ2＝1，则：

2.权具有的性质

①权愈大表示观测值愈可靠，即精度愈高；

②权始终取正号；

③权是一个相对性数值，因此，对于单独一个观测值来讲无意义；

④权可用同一数乘或除，而不会改变其性质。

3.权与中误差的关系

（1）权与中误差的区别。

权与中误差都是精度指标，都能衡量观测值之间精度的高低。中误差属一组观测值的绝对精度指标；权属一组观测值的相对精度指标，这一组观测值可以是同类性质的观测值，也可以是不同类性质的观测值。

（2）权与中误差的联系。(www.xing528.com)

观测值精度愈高，可靠程度愈大，它的权就愈大，而观测值的中误差愈小；反之亦然。

4.单位权

为便于由中误差求权，假定某一观测结果的权为1，这p＝1的权称为单位权。对应于权等于1的观测值，称为单位权观测值；对应于权等于1中误差称为单位权中误差。单位权中误差通常用u表示，即u＝m1。

p1u2＝p2m22＝…＝pnm2n＝μ2

利用p1＝1，可知单位权中误差u为：

在不等精度观测中，每个观测值精度都不同，因此应先求出单位权中误差u，然后再利用（6.18）式求出各观测值的中误差。

单位权只起一个比例常数的作用，它的值可任意选定；但对于同一量的p值不能选两个不同的u值，以免破坏权的比例关系。

5.加权算术平均值

设对某一未知量进行了n次非等精度的观测，观测值分别为l1，l2，…，ln，各观测值相应的权为p1，p2，…，pn。测量上取其加权算术平均值作为非等精度观测值的最可靠值，即最或是值。

加权算术平均值x0为

6.3.3 计算实例

按中误差来确定权是定权的基本方法，但对于某些测量工作则可用更简便的方法来确定权。

1.角度测量观测值权的确定

例6.6 设用一测回测角中误差为m的经纬仪，对某角进行了N次非等精度观测， L1，L2，L3分别为同精度观测了n1，n2，n3次后的算术平均值，求L1，L2，L3的权。

解：设观测值L1，L2，L3的中误差分别为：m1，m2，m3，根据误差传播定律：

按（6－18）式相应的权为：

则

pi＝c·ni

结论：在角度测量中，所测得各角的权pi与该角的观测次数ni成正比。

在角度测量中，可根据测回数来确定权。如n1，n2，n3分别为3，4，5测回时，选c＝1，则：p1＝cn1＝3，p2＝cn2＝4，p3＝cn3＝5。

c＝1表示＝1，故u＝m，即单位权中误差就是观测一次的中误差。

2.距离测量观测值权的确定

例6.7 设在同样的情况下丈量了三段距离D1，D2，D3，已知每公里的中误差为m，试确定D1，D2，D3的权。

解：根据误差传播定律，D1，D2，D3的中误差分别为：

按（6－18）式相应的权为：

结论：距离的权pi与它的长度Di成反比。

在距离丈量中，可根据距离长短来确定权。如D1，D2，D3分别为4km，6km，7km，选c＝4，则：p1＝＝1，p2＝＝23，p3＝＝47

c＝4，p1＝1，表示D1的权为1，即丈量4km长的权为1，丈量4km长的中误差为单位权中误差。

3.水准测量中路线高差观测值权的确定

例6.8 如图6.4所示，设有一个节点水准网，已知A，B，…，K个水准点的高程，由几条同一等级的水准路线测定E点的高程，各条水准路线的测站数分别为N1， N2，…，Nn，高差分别为h1，h2，…，hn，各条水准路线相应的权为p1，p2，…，pn，每一测站高差的中误差为m站，试确定各水准路线的权。

图6.4 节点水准网

解：根据误差传播定律，h1、h2、…、hn的中误差分别为：

按（6－18）式相应的权为：

结论：在山地进行水准测量时，路线高差观测值的权pi与路线的测站数Ni成反比，即不同路线的高差观测值可用路线测站数的倒数定权。

同理可知，在平地进行水准测量时，路线高差观测值的权pi与路线的千米数Li成反比，即不同路线的高差观测值可用路线千米数的倒数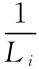定权。

例6.9 如图6.5所示，沿三条路线按每千米中误差相等的方法，分别测定D点高程，三条水准路线的路线长度分别为：L1＝4km，L2＝6km，L3＝5km，试确定三条水准路线的权。

图6.5 节点水准测量

解：选定c＝6，则：