视距测量的基本步骤和误差影响

视距测量是利用望远镜内十字丝分划板上的视距丝在视距尺（或水准尺）上进行读数，根据几何光学和三角学原理，同时测定水平距离和高差的一种方法。普通视距测量的相对精度为1／200～1／300，只能满足地形测量的要求，主要用于地形测量中。

4.2.1 视距测量的原理

1.视准轴水平时的视距公式

常规测量的望远镜内都有视距丝装置。从视距丝的上、下丝a2和b2（见图4.8）发出的光线在竖直面内所夹的角度Φ是固定角。该角的两条边在尺上截得一段距离aibi＝li （称为尺间隔）。由图可以看出，已知固定角Φ和尺间隔li即可推算出两点间的距离（视距）Di＝cotφi。因Φ保持不变，尺间隔li将与距离Di成正比例变化。这种测距方法称为定角测距。经纬仪、水准仪和全站仪等都是以此来设计测距的。

图4.8 视准轴水平时的视距测量

如图4.8所示，尺间隔li＝1.490－1.289＝0.201m。

2.视准轴倾斜时的视距公式

在地面起伏较大的地区进行视距测量时，必须使视线倾斜才能读取视距间隔。由于视线不垂直于视距尺，故不能直接应用上述公式。

设想将目标尺以中丝读数l这一点为中心，转动一个α角，使目标尺与视准轴垂直，由图4.9可推算出视线倾斜时的视距测量计算公式

D＝Kl·cos2α 　（4－13）

h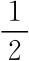＝Klsin2α＋i－v 　（4－14）

式中：K为视距常数；α为竖直角；i为仪器高；v为中丝读数即目标高。

图4.9 视准轴倾斜时视距测量

4.2.2 视距测量的方法

欲计算地面上两点间的距离和高差，在测站上应观测i、l、v、α四个量。所以，视距测量通常按下列基本步骤进行观测和计算。

①在A点安置经纬仪，量取仪器高i，在B点竖立水准尺。

②盘左位置，转动照准部瞄准B点水准尺，分别读取上、下、中三丝读数，并算出尺间隔l。

③转动竖盘指标水准管微动螺旋，使竖盘指标水准管气泡居中，读取竖盘读数，并计算垂直角α。

④根据公式计算出水平距离和高差。

4.2.3 视距测量的误差来源及注意事项

1.视距测量的误差(www.xing528.com)

影响视距测量精度的因素主要有以下几个方面：

（1）视距丝读数误差。

视距丝读数误差是影响视距测量精度的重要因素，它与尺子最小分划的宽度、距离的远近、望远镜的放大率及成像清晰情况有关。因此读数误差的大小，视具体使用的仪器及作业条件而定。由于距离越远误差越大，所以视距测量中要根据精度的要求限制最远视距。

（2）视距尺分划的误差。

如果视距尺的分划误差是系统性的增大或减小，对视距测量将产生系统性的误差。这个误差在仪器常数检测时将反映在视距常数K上。即是否仍能使K＝100，只要对K加以测定即可得到改正。

如果视距尺的分划误差是偶然性误差，即有的分划间隔大，有的分划间隔小，那么它对视距测量也将产生偶然性的误差影响。如果用水准尺进行普通视距测量，因通常规定水准尺的分划线偶然中误差为±0.5mm，所以按此值计算的距离误差为：md＝k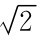（×0.5）＝0.071m。

（3）视距常数K不准确的误差。

一般视距常数K＝100，但由于视距丝间隔有误差，标尺有系统性误差，仪器检定有误差，会使K值不为100。K值误差会使视距测量产生系统误差。K值应在100±0.1之内，否则应加以改正。

（4）竖角观测的误差。

由距离公式D＝klcos2α可知，α有误差必然影响距离，即md＝k/sin2α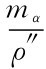。设kl＝100m，α＝45°，mα＝±10″，则md≈±5mm。可见竖直角观测误差对视距测量影响不大。

（5）视距尺竖立不直的误差。

如果标尺不能严格竖直，将对视距值产生误差。标尺倾斜误差的影响与竖直角有关，影响不可忽视。观测时可借助标尺上水准器保证标尺竖直。

（6）外界条件的影响。

外界环境的影响主要是大气垂直折光的影响和空气对流的影响。大气垂直折光的影响较小，可用控制视线高度削弱，测量时应尽量使上丝读数大于1m。同时选择适宜的天气进行观测，可削弱空气对流造成成像不稳甚至跳动的影响。

2.注意事项

①观测时应抬高视线，使视线距地面在1m以上，以减少垂直折光的影响。

②为减少水准尺倾斜误差的影响，在立尺时应将水准尺竖直，尽量采用带有水准器的水准尺。

③水准尺一般应选择整尺，如用塔尺，应注意检查各节的接头处是否正确。

④竖直角观测时，应注意将竖盘水准管气泡居中或将竖盘自动补偿开关打开，在观测前，应对竖盘指标差进行检验与校正，确保竖盘指标差满足要求。

⑤观测时应选择风力较小，成像较稳定的情况下进行。