黏土层固结过程中的应力转化技术

从上述固结模型模拟的土体中某点固结过程可以看出：固结过程是饱和土体在某一压力作用下，土体中的超孔隙水应力不断消散、有效应力相应增加的过程，或者说是超孔隙水应力逐渐转化为有效应力的过程。现在讨论在某一压力p作用下、饱和黏土层某一竖向截面上任一时刻t、任一深度z这种应力转化的过程。

1.边界条件

所讨论的可压缩土层为饱和黏性土层，它在自重作用下的固结已经完成。土的压缩和固结仅在竖直方向发生，在固结过程中，孔隙水的渗流只沿竖直方向进行，为单向渗透固结。

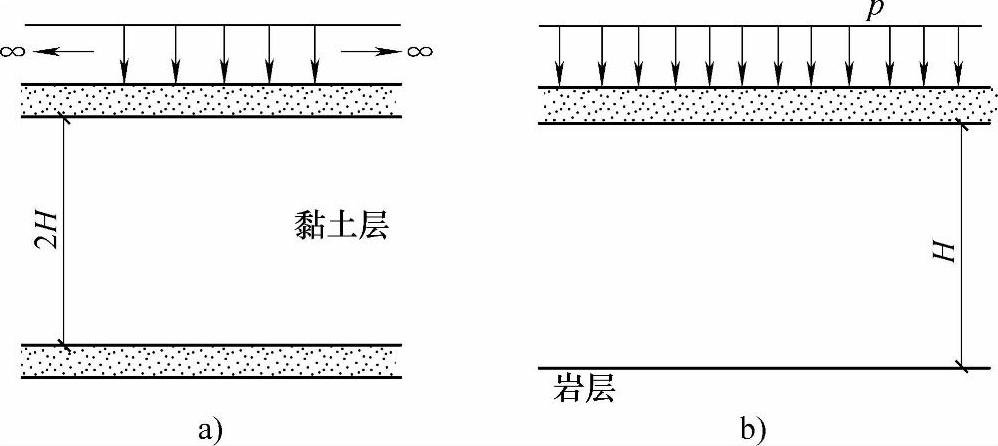
图6.4.4 饱和黏性土层的边界条件

a）单向双面渗透 b）单向单面渗透

如图6.4.4所示，该土层的顶、底面排水条件有两种情况。

图6.4.4a表示厚度为2H的饱和黏土层，其顶面是透水的，底面则是透水的不可压缩层，水能向上、向下作单向双面渗透。

图6.4.4b表示厚度为H的饱和黏土层，其顶面是透水的，底面是不透水的不可压缩层，水只能向上作单向单面渗透。

2.初始条件

地表上一次施加着满布的均匀荷载p，荷载面积远大于压缩土层的厚度，土中的附加应力σ_z=p，并沿深度均匀分布，如图6.4.5所示。

图6.4.6列出单向单面渗透的饱和黏性土层，地表上满布均匀荷载p，任一深度z的土层在三种特定时刻的应力分布。

1）t=0，骤然加上荷载p，由于透水性差，孔隙水未能立即被挤出，荷载p完全由孔隙水承受。孔隙水压力的分布如图6.4.6a中的abce所示。

2）0＜t＜∞，随着时间t的延伸，孔隙水逐渐向上从顶面排出，孔隙水压力u就逐渐减小，有效应力σ′随之增加。图6.4.6b中的ad线表示某一时刻有效应力σ′和孔隙水压力u沿深度的变化曲线。

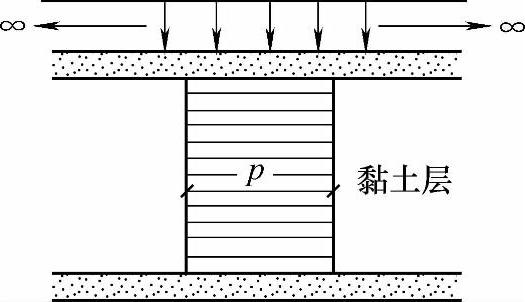
图6.4.5 土中的附 加应力分布

3）t=∞，ad与ae重合，即σ′=σ_z=p及u=0，这时，附加应力完全由土的骨架承受。有效应力σ′的分布如图6.4.6c中的abcd所示。

由图6.4.6的讨论，可知σ′、u的分布曲线已知，土中有效应力σ′和孔隙水压力u是深度z和时间t的函数，即

σ′=f（z，t） （6.4.3）

u=F（z，t） （6.4.4）

当t=0时，即σ′=f（z，t）=0及u=F（z，t）=σ_z=p，也就是附加应力完全由孔隙水压力u承受。

当t=∞时，即σ′=f（z，t）=σ_z=p及u=F（z，t）=0，也就是附加应力完全由有效应力σ′承受。

图6.4.7列出该土层在0＜t＜∞阶段的不同时间t，黏土层内孔隙水应力沿z方向的分布。可以看到排水距离是影响超孔隙水应力消散的一个重要因素，土层顶面的排水距离最短，故顶面的超孔隙水应力最早被转化为有效应力，土层底面排水距离最长，故底面的超孔隙水应力最后才被转化为有效应力。

图6.4.8列出了双面渗透饱和黏性土层，当地表上满布均匀荷载p，任一深度z土层在7种特定时刻的应力分布示意图，图中所示虚线为各级荷载的孔隙水应力分布线。

当t=0时，附加应力完全由孔隙水压力u承受；

当t=∝时，附加应力完全由有效应力σ′承受。

当t₀＜t₁＜t₂＜t₃＜t_∝时，土层顶面和底面的排水距离最短，故孔隙水应力最早被转化为有效应力；土层中点排水距离最长，故孔隙水应力最后才被转化为有效应力。

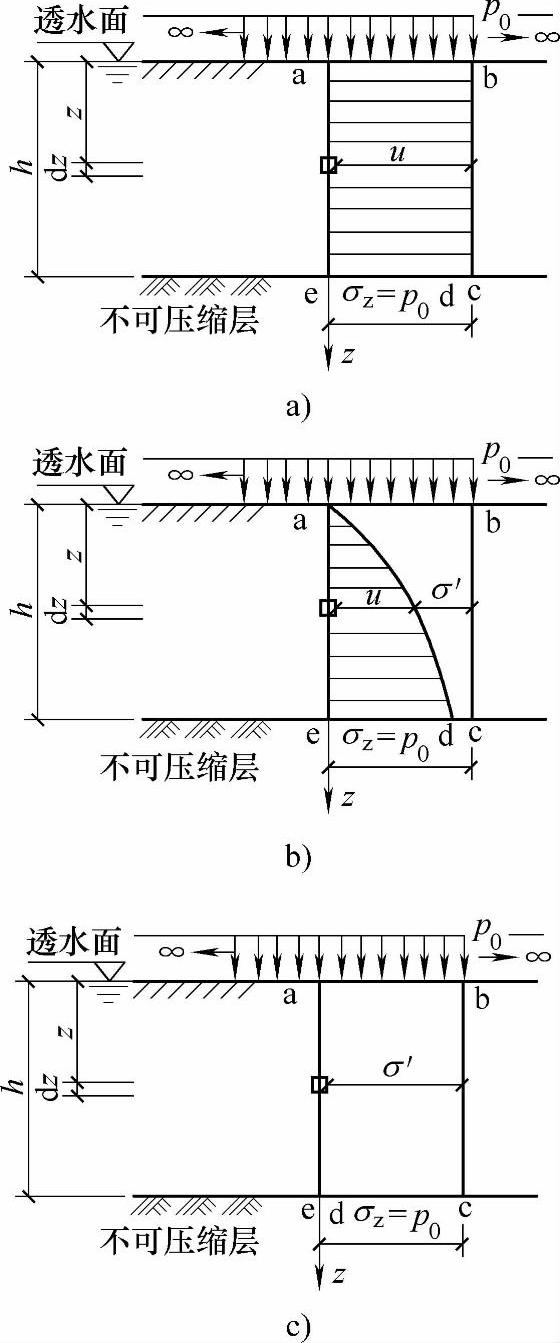
图6.4.6 三种特定时刻的应力分布

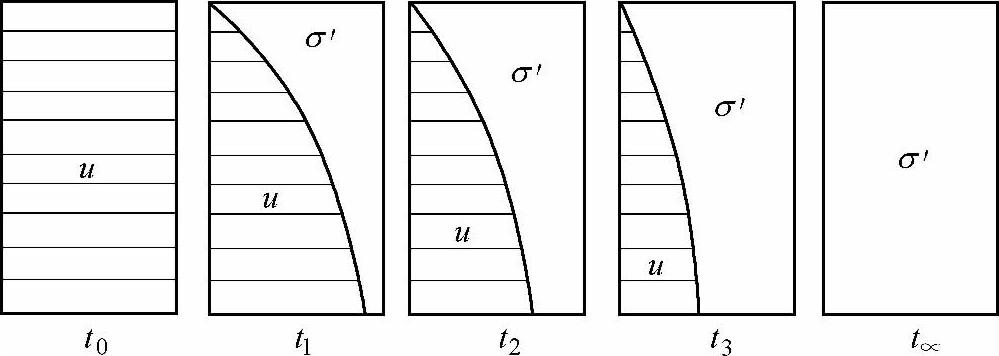
图6.4.7 0＜t＜_∞阶段应力分布的演变 （t₀＜t₁＜t₂＜t₃＜t_∞）

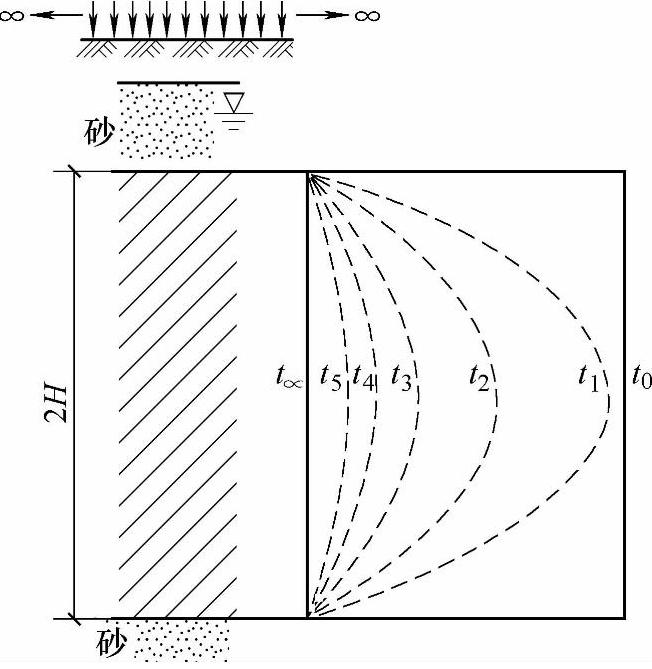
图6.4.8 双面渗透饱和黏性土层的应力分布演变

3.固结度

（1）深度z处的固结度U_z。地基的固结度是指地基固结的程度。就是指在某一附加应力p作用下，某一深度z处土层，经某一段时间t后，土体发生固结的程度，用U_z，t表示。

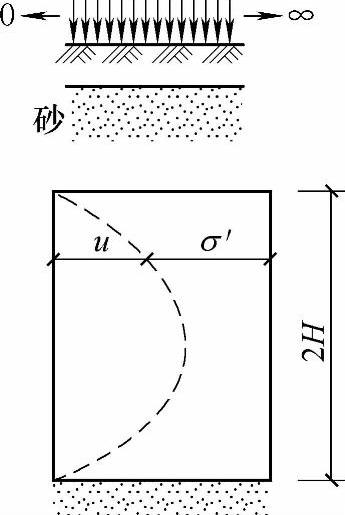
图6.4.9 某一时刻的应力面积

图6.4.9列出经某一段时间t后，某一深度z处土层处受到的有效应力σ′和孔隙水压力u增长的程度。此处，σ=σ′+u。

这时的固结度U_z，t可用该黏土层有效应力的增长程度来表示

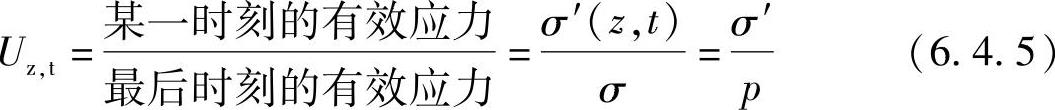
式中 σ′（z，t）——某一时刻的有效应力；

σ——最后时刻的有效应力，其大小即等于该点的附加应力σ=p。

固结度U_z，t亦可用黏土层孔隙水应力消散的程度来表示，

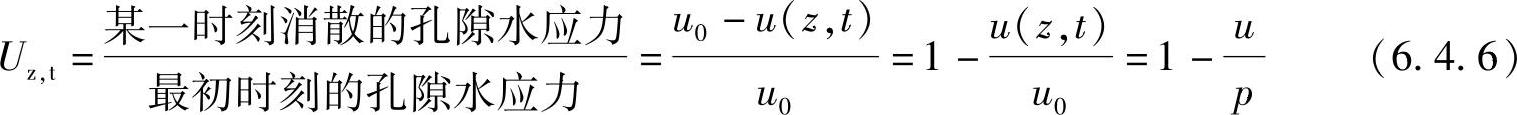
式中 u（z，t）——某一时刻的孔隙水应力；

u₀——最初时刻的有效应力，其大小即等于该点的附加应力u₀=p；

u₀-u（z，t）——某一时刻消散的孔隙水应力。

（2）平均固结度U_t。某一点的固结度对于解决工程实际问题来说并不重要，重要的是整个土体的固结度，为此，引入土层平均固结度的概念。土层的平均固结度可用某一时刻有效应力面积与最终时刻有效应力面积之比来表示，图6.4.9表示某一时刻有效应力和孔隙水应力的应力面积，从图中可得平均固结度U_t的表达式为

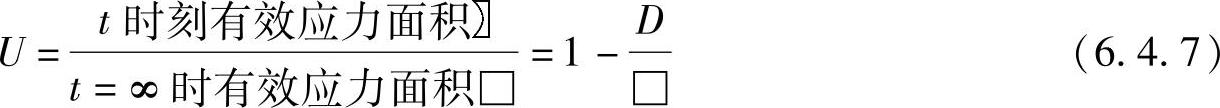
其数学表达式为

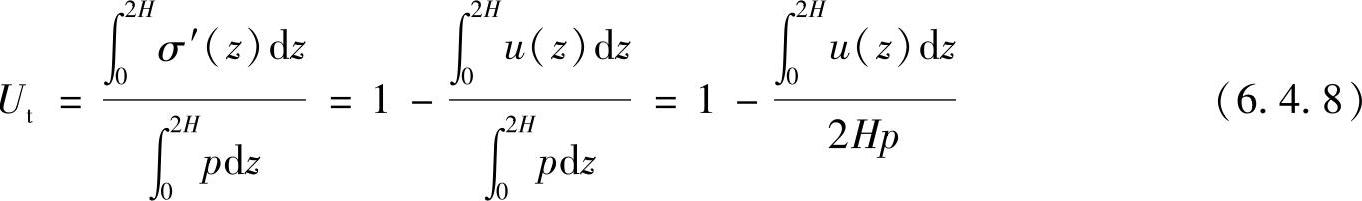
上式表明土层的固结度也就是土中孔隙水压力向有效应力转化过程的完成程度。

可以采用应力面积法计算固结沉降量s，其表达式为

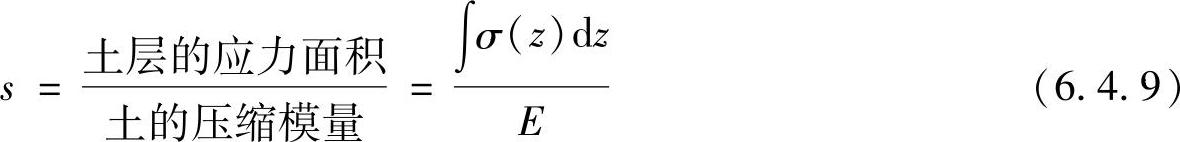
土层的固结沉降与该层的有效应力面积成正比，故上式也能表示为

式中 s_t——地基在任意时刻t的固结沉降量；

s——最终的沉降量。

平均固结度也可用土体压缩变形量定义为：地基土在荷载作用下，经历一段时间后产生的固结沉降量和最终沉降量的比值（或用固结百分数表示）。

由上式可知，当t=0时，s_t=0，则U_t=0（或0%）；当固结稳定时，即t=∝时，s_t=s，则U_t=1.0（或100%），即固结度变化范围为0～1，它表示在某一荷载作用下经过t时间后土体所能达到的固结程度。(www.xing528.com)

【6.4.1】 （2012年岩土考题）

某厚度6m的饱和软土层，采用大面积堆载预压处理，堆载压力p₀=100kPa，在某时刻测得超孔隙水压力沿深度分布曲线如图6.4.10所示，土层的E_s=2.5MPa，k=5.0×10^-8cm/s。

试求此时刻饱和软土的压缩量最接近下列哪个数值？（总压缩量计算经验系数取1.0）（mm）

（A）92 （B）118 （C）148 （D）240

【答案】 （C）

【解答】 （1）土层平均固结度。

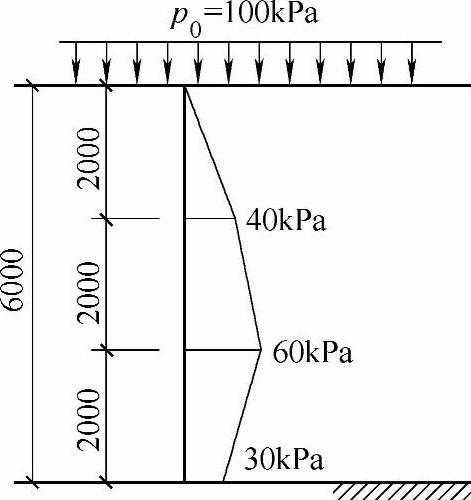
图 6.4.10

（2）软土层最终总压缩量。

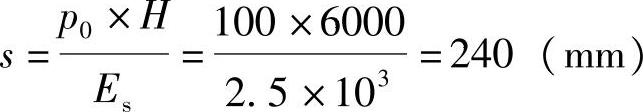
（3）此刻饱和软土的压缩量。

s_t=s·U_t=240×0.617=148（mm）

故选（C）。

（3）固结度计算的普遍表达式。

若荷载作用面积较大，或土层较薄时，附加应力在地基渗透固结深度范围内分布是均匀的，对式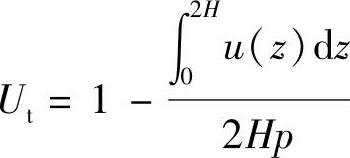积分后，经过简化得到适用于U_t＞30%时的计算公式

U_t=1-α·e^-βt （6.4.11）

式中，参数α、β的具体取值见《建筑地基处理技术规范》表5.2.7的规定

式中 c_v为固结系数。

（4）固结系数。

上述的固结度计算的普遍表达式为

U_t=1-α·e^-βt （6.4.13）

在竖向排水固结的情况下，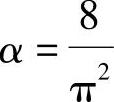

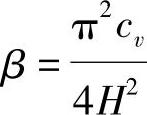
可知影响固结度的主要参数是：时间长短t、土的厚度H和固结系数c_v。

竖向固结系数c_v可按下式计算

式中 k——土的渗透系数（m/a）；

e_m——饱和黏性土在固结过程中的平均孔隙比；

α——土的压缩系数（MPa^-1）。

现将固结系数c_v中的“渗透系数”、“孔隙比”、“压缩系数”三项参数的内容作简要介绍。

1）渗透系数k。由于土的骨架颗粒之间存在的孔隙构造了水的通道，在水头差的作用下，水将在土体内部相互贯通的孔隙中流动，称为渗流（渗透）。

由水力学知识知道，水在土中渗流满足达西定律，即

V=ki

式中 V——渗流速度，土中单位时间内流经单位横断面的水量（m/s）；

i——水力梯度，沿渗透途径出现的水头差Δh与相应渗流长度L的比值，i=Δh/L；

k——渗透系数（m/s）。

由上式可以看出，当水力梯度为定值时，渗透系数越大，渗流速度就越大；当渗流速度为定值时，渗透系数越大，水力梯度越小。由此可见，渗透系数与土的透水性强弱有关，渗透系数越大，土的透水能力越强。

2）孔隙比e。土的孔隙比是土中孔隙体积V_v与土粒体积之比，即

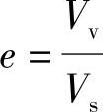
图6.4.11采用三相图表示孔隙体积V_v与土粒体积V_s间的关系，如图6.4.11所示，令V_s=1，则V_v=e，V=1+e。

孔隙比用小数表示。可以用来评价天然土层的密实程度。一般e＜0.6的土是密实的或低压缩性的，e＞1.0的土是疏松的或高压缩性的。

3）压缩系数α。通过室内侧限压缩试验可以求得在各级压力下孔隙比的大小，各级压力与其相应的稳定孔隙比之间的曲线叫做压缩曲线，或简称e—p曲线（图6.4.12）。

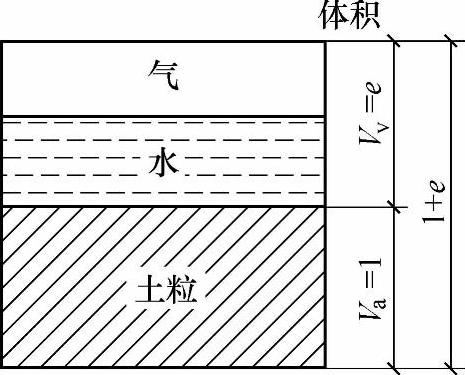
图6.4.11 三相图表示孔隙比

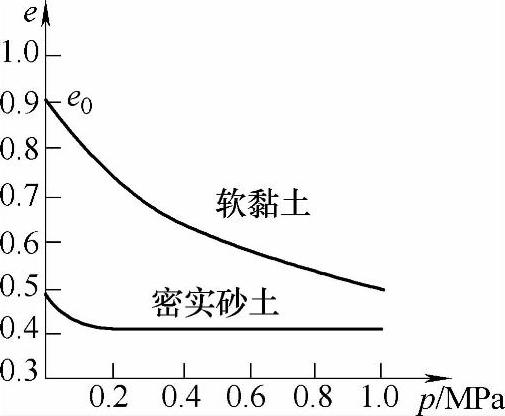
图6.4.12 压缩曲线

压缩曲线具有如下特点：非线性，弹塑性，只有体缩没有体胀，曲线陡缓代表压缩性的大小，反映了土的压缩特性。

如图6.4.13所示的e-p曲线，设压力由p₁增至p₂，相应的孔隙比由e₁减小到e₂。土的压缩性可用这一段压力范围的割线的斜率α来表示，α称压缩系数（MPa^-1）。

式中 p₁，p₂——固结压力；

e₁，e₂——相应于p₁、p₂时的孔隙比。

土的压缩系数并不是常数，而是随压力p₁、p₂的大小改变而变化，压缩系数越小，土的压缩性就越小。

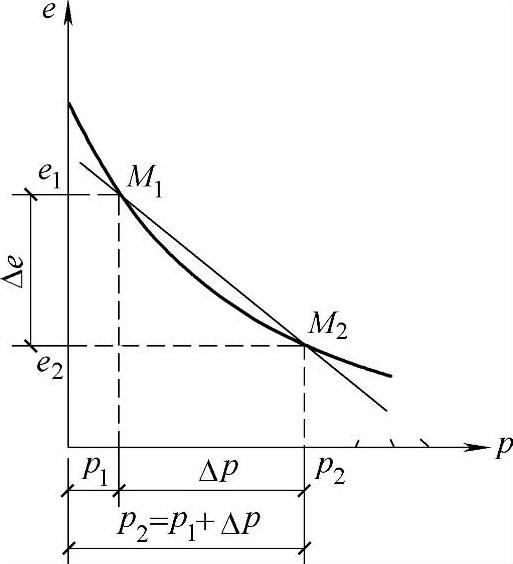
图6.4.13 e-p压缩曲线图

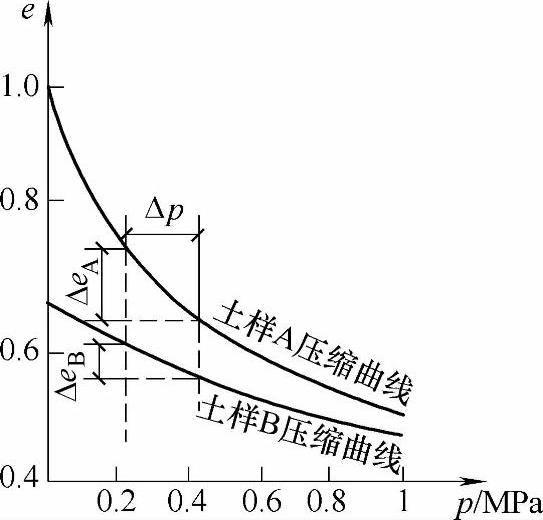
图6.4.14 压缩曲线比较

土的压缩曲线可以反映土的压缩性质。图6.4.14表示两种土样A和B的压缩曲线，土样A的压缩曲线较陡，土样B的压缩曲线较平缓，在同一压力增量Δp的作用下，土样A的Δe_A变化较大，而土样B的Δe_B变化较小；所以土样A就比土样B的压缩变形大，土也较软，因此，可用土的压缩曲线的斜率来衡量土的压缩性。