直线与平面、平面与平面的相对位置有平行、相交和垂直3种情况(垂直属于相交的特殊情况)。
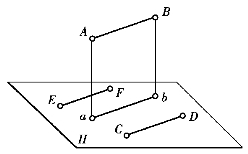
图1.101 直线和平面平行的条件
1)直线与平面、平面与平面平行
(1)直线与平面平行
若直线平行于平面上的任一直线,则此直线必与该平面平行。如图1.101所示,直线AB与平面H上的任一直线CD(或EF)平行,则AB∥H面。
【例1.18】 如图1.102所示,过△ABC外一点D,作一条水平线DE与△ABC平行。
【解】 求作水平线DE与△ABC平行,可以先在△ABC上作一条水平线,使DE与该直线平行,则DE∥△ABC,DE与该水平线的同面投影必平行。
解题步骤如图1.102(b)、图1.102(c)所示:
①在△ABC上作一水平线BF(b′f′、bf);
②过d′作直线d′e′∥b′f′,过d作de∥bf,则DE即为所求。
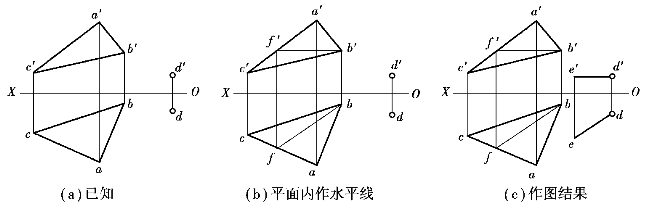
图1.102 过已知点作水平线平行于已知平面
判别直线是否与平面平行,可归结为在平面上能否作出一直线与该直线平行。
【例1.19】 如图1.103(a)所示,已知ABCD平面外一直线MN,判别MN是否与该平面平行。
【解】 如图1.103(b)所示,在ABCD平面的V面投影图上作直线b′e′∥m′n′并与c′d′相交于e′,由e′求得e,连直线be,因为be∥mn,所以MN与平面ABCD平行。
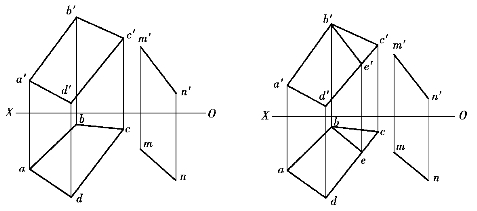
图1.103 判别直线与平面是否平行
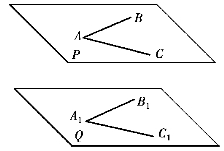
图1.104 两平面平行的条件
(2)平面与平面平行
若一平面上的相交两直线与另一平面上的相交两直线对应平行,则该两平面互相平行。如图1.104所示,P平面内的两条相交直线AB、AC分别平行于Q平面内的两条相交直线A1B1、A1C1,则P平面平行于Q平面。
【例1.20】 如图1.105(a)所示,判别△ABC和△DEF两平面是否相互平行。
【解】 要判断两平面是否平行,就要看在两平面上能否找到一对相交直线对应平行。
在△ABC上的一点A作相交两直线AG和AK,使它们的V面投影a′g′∥d′e′,a′k′∥d′f′,由a′g′和a′k′作出ag和ak,因为ag∥de,但ak∥df,所以△ABC∥△DEF。
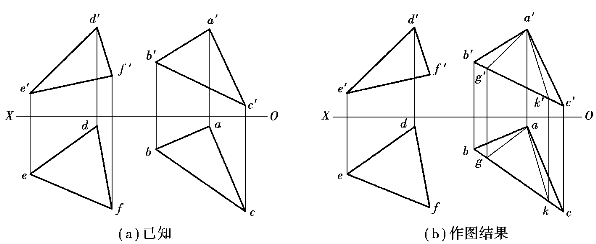
图1.105 判别两平面是否平行
【例1.21】 如图1.106(a)所示,过点K作一平面与平行两直线AB和CD所决定的平面平行。
【解】 在已知平面上先连接AC,使该平面转换为由相交两直线AB和AC所决定的平面,再过k′作k′e′∥a′b′,k′f′∥a′c′,过k作ke∥ab、kf∥ac,相交两直线KE和KF所决定的平面即为所求。
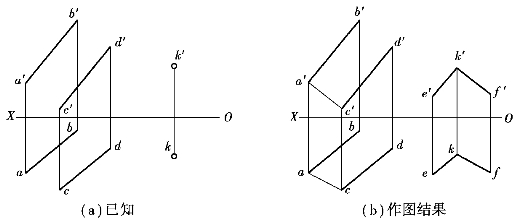
图1.106 过已知点作平面与已知平面平行
2)直线与平面、平面与平面相交
直线与平面或平面与平面之间,若不平行则必相交。直线与平面相交产生交点;平面与平面相交产生交线,交线是一条直线。
直线与平面相交的交点是直线与平面的共有点,该点既在直线上又在平面上。求解交点的投影,则需利用直线和平面的共有点或在平面上取点的方法。平面与平面的交线是一条直线,是两平面的共有线,求交线时只要先求出交线上的两个共有点(或一个交点和交线的方向),连之即得。在投影图中,为增强图形的清晰感,必须判别直线与平面、平面与平面投影重叠的那一段(称重影段)的可见性。
(1)投影面垂直线与一般位置平面相交
利用投影面垂直线的积聚性,可直接求出交点。
【例1.22】 如图1.107(a)所示,求作铅垂线EF与一般位置平面△ABC的交点。
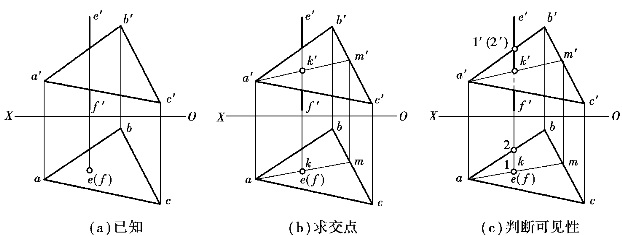
图1.107 铅垂线与一般面相交
【解】 因为平面与直线的交点可以看成直线上的点,利用直线在H面的积聚性投影可直接找到交点K的H面投影k,再利用面上取点的方法即可求出k′。对V面上线面投影重影段的可见性,必须利用交叉直线重影点的可见性来判别。
①求交点的投影:如图1.107(b)所示。
②判断可见性:a′b′及a′c′与e′f′的交点均为重影点,可任选其中的一点如1′(2′),它们是AB上的Ⅱ点与EF上的Ⅰ点在V面上重影。由其H面投影可知,Ⅰ点在前,即e′k′段可见,而k′f′的则为不可见(画虚线)。(https://www.xing528.com)
(2)一般位置直线与投影面垂直面相交
利用投影面垂直面的积聚性投影,即可直接求出交点。
【例1.23】 如图1.108所示,求铅垂面ABC与一般位置直线DE的交点,并判别可见性。
【解】 因K在DE上,k必在de上;又因K在△ABC上,故k必积聚在△ABC的H面投影abc上,即k必是de与abc的交点。由k作OX轴的垂线与d′e′相交于k′,K(k′,k)即为所求。
又因直线DE穿过△ABC,在交点K之前的一段为可见,交点K之后则有一段被平面遮挡而为不可见,显然交点K为可见与不可见段的分界点。由于铅垂面的H面投影有积聚性,故可根据它们之间的前后关系直接判别其V面投影的可见性。
①求交点:如图1.108(b)所示。
②判断可见性:如图1.108(c)所示,ke一段均在k之前,k′e′为可见,而k′之后的重影段为不可见(画虚线)。对H面投影的可见性,因投影具有积聚性,无须判别其可见性。
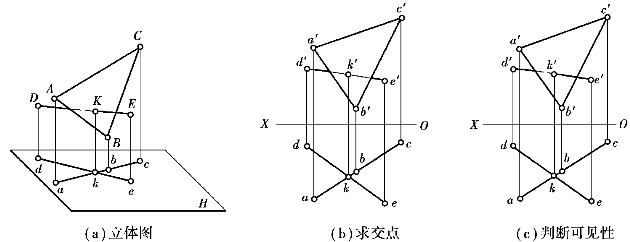
图1.108 求直线与投影面垂直面的交点
(3)一般位置平面与投影面垂直面相交
【例1.24】 如图1.109(a)所示,求铅垂面ABC与一般面DEF的交线,并判别可见性。
【解】 在【例1.23】的基础上增加直线EF,而构成相交两直线所表示的一般面与铅垂面△ABC相交,求其交线。显然,这是上一问题的叠加。可同前求出交线上的一点K(k′,k)后,再求EF与△ABC的交点M(m′,m),连KM(k′m′,km)即为所求。
关于可见性的判别,是在上述的线面相交可见性的基础上进行,显然交线一般情况下,属可见,而且是两平面投影重叠处可见与不可见的分界线,即两平面投影重叠处被分为两部分,交线一侧为可见,另一侧为不可见。又已知两平面周界边线之间均为交叉直线,且每一对交叉直线中,若一条边线为可见,另一条必不可见。由此对V面可见性的判别,因ED、EF两直线为同一平面,故交点M(m′,m)之后的一段也和K(k′,k)之后一样,均为不可见。这时又由于e′k′可见,即e′m′亦为可见,则与之交叉的重叠段b′c′为不可见(画虚线)。同理,可判别其余部分的可见性。
解题步骤如图1.109所示。
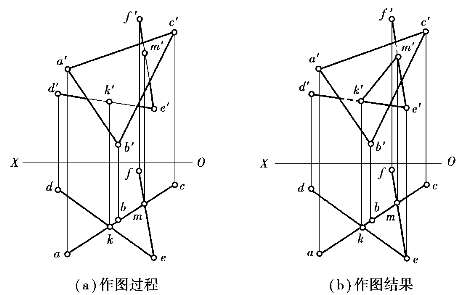
图1.109 一般面与铅垂面相交
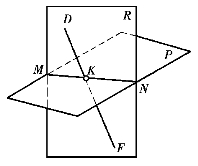
图1.110 一般位置直线与 一般位置平面的交点求法
(4)一般位置直线与一般位置平面相交
由于一般位置直线、面的投影没有积聚性,不能在投影图上直接定出其交点。如图1.110所示,求交点时,可采用辅助平面进行作图:
①包含直线DF作辅助平面R;
②求平面P与辅助平面R的交线MN;
③求出交线MN与直线DF的交点K,即为所求。
为作图方便,常取投影面垂直面作为辅助平面。
【例1.25】 如图1.111(a)所示,求直线DF与△ABC的交点,并判别其可见性。
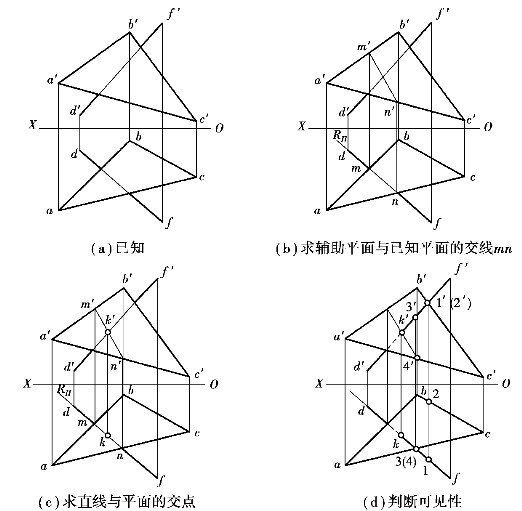
图1.111 一般位置直线与一般位置平面相交
【解】 解题步骤如下:
①包含DF作一辅助铅垂面R,这时df与RH重合;
②求辅助平面R与△ABC的交线MN(m′n′,mn);
③m′n′与d′f′相交于k′,即为所求交点K(k′,k)的V面投影,可在df上定出k,即为所求交点K的H面投影;
④利用重影点,判别其投影重合部分的可见性。
(5)两个一般位置平面相交
【例1.26】 如图1.112(a)所示,求一般面△ABC与一般面△DEF的交线,并判别其可见性。
【解】 如图1.112(a)所示,可看作是在【例1.25】的基础上,添加一直线DE而形成相交两直线所表示的一般面与△ABC相交,求交线。可分别求出DF、DE与△ABC相交的两个交点再连接两个交点完成两平面相交的交线。
①完成交点K(k′,k)的投影:求作方法同【例1.25】,如图1.112(b)所示。
②同理,可求出DE与△ABC的交点G(g′,g),如图1.112(c)所示。
③连接KG(k′g′,kg),即为所求的交线,如图1.112(d)所示。
④判断可见性。根据重影点判别两平面投影重合部分的可见性。交线是可见不可见的分界线,同面相邻边的可见性相同,异面相邻边的可见性相反,如图1.112(d)所示。
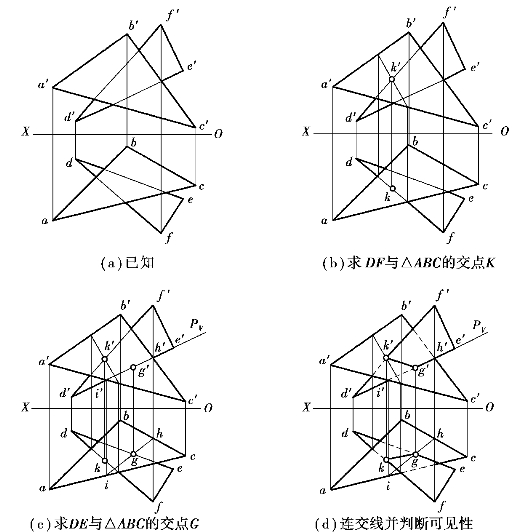
图1.112 两个一般位置平面相交
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




