试验设计与统计分析：一元线性回归

一、回归分析的概念与特点

1.回归分析的概念

回归分析就是对具有相关关系的两个变量之间的数量变化的一般关系进行测定，确定一个与之相应的数学表达式，以便进行估计和预测的一种统计方法。

2.回归分析的特点

（1）回归分析的两个变量是非对等关系。在回归分析中，两个变量之间哪一个是因变量哪一个是自变量，要根据研究目的的具体情况来确定。自变量、因变量不同，所得出的分析结果也不相同。而在相关分析中，相关关系的两个变量是对等的，不必区分哪一个是自变量，哪一个是因变量。

（2）在回归分析中，因变量Y是随机变量，自变量X是可控变量。可依据研究的目的，分别建立对于X的回归方程或对于Y的回归方程；而相关分析中，被研究的两个变量都是随机变量，它只能通过计算相关系数来反映两个变量之间的密切程度。

3.回归分析的类型

回归分析研究两个及两个以上的变量时，根据变量的地位、作用不同，分为自变量和因变量。一般把作为估测根据的变量叫做自变量，把待估测的变量叫做因变量。反映自变量和因变量之间联系的数学表达式叫做回归方程，某一类回归方程的总称为回归模型。在回归分析中根据研究的变量多少可以分为一元回归和多元回归。若只有一个自变量和一个因变量的回归称为一元回归或简单回归。若自变量的数目在两个或两个以上，因变量只有一个，则称为多元回归。根据所建立的回归模型的形式，又可以分为线性回归和非线性回归。

4.回归分析的内容

（1）建立回归方程 依据研究对象变量之间的关系建立回归方程。

（2）进行相关关系的检验 相关关系检验就是选择恰当的相关指标，判定所建立的回归方程中变量之间关系的密切程度。相关程度越高，就表明回归方程与实际值的偏差越小，拟合效果越好。如果回归方程变量间的相关关系不好，所建立的回归方程就失去了意义。

（3）利用回归模型进行预测 如果回归方程拟合得好，就可以用它来做变量的预测，根据自变量取值来估计因变量的值。由于回归方程与实际值之间存在误差，预测值不可能就是由回归方程计算所得的确定值，其应该处于一个范围或区间。这个区间称为预测值的置信区间，它说明回归模型的适用范围或精确程度。实际值位于该区间的可靠度一般应在95%以上。

5.相关分析与回归分析的区别与联系

就其研究对象来说，它们都是研究变量之间的相互关系。但是相关分析与回归分析存在着明显的区别：相关分析泛指两个变量之间存在相关关系时，不必指出何者是自变量或因变量，两个变量是对等关系，都是随机变量；在回归分析中，必须根据研究目的，分别确定其中的自变量和因变量，两个变量是不对等关系，其中因变量是随机变量，而自变量是非随机变量。二者研究的侧重点不同。相关分析主要是研究变量之间是否存在相关关系及相关关系的表现形式和密切程度；而回归分析是运用一定的回归模型来测定一个或几个自变量的变化对因变量数量变化的影响。本书着重介绍一元线性回归分析。

二、一元线性回归分析

1.一元线性回归模型

一元线性回归模型也称简单线性回归模型，是分析两个变量之间相互关系的数学方程式，其一般表达式

式中：代表因变量y的估计值；x代表自变量，a、b称为回归模型的待定参数，其中 b又称为回归系数，它表示自变量每增加一个单位时，因变量的平均增减量。

用x_i表示自变量x的实际值，用y_i表示因变量y的实际值（i=1，2，3，…，n），因变量的实际值与估计值之差用e_i表示，称为估计误差或残差。即：e_i=。

依据最小平方理论可得

由以上两式即可求出a，b的计算公式

上述回归方程式在平面坐标系中表现为一条直线，即回归直线。当b＞0时，y随x的增加而增加，两变量之间存在着正相关关系；当b＜0时，y随x的增加而减少，两变量之间为负相关关系；当b=0时，y为一常量，不随x的变动而变动。这为判断现象之间的相互关系，分析现象之间是否处于正常状态提供了标准。

【例7-3】应用表7-1的资料建立一元线性回归模型。

设年广告费为自变量x，年销售收入因变量y，则有

依据式7-10数据可得

一元线性回归方程计算表，如表7-5所示。

表7-5 一元线性回归方程计算表

一元线性回归方程为

y=48.2143+1.1429x

方程中a=48.2143为初始水平，b=1.1429为回归系数。该方程表明年广告费每增加一万元，年销售收入将会增加1.1429万元。

2.一元回归模型的检验

（1）相关系数及其显著性检验 一般说来，相关系数可以反映自变量x和因变量y之间的线性相关程度，相关系数r的绝对值越接近于1，则x与y之间的线性关系越密切。但相关系数通常是根据总体的样本数据计算得出，带有一定的随机性，会出现误差，因而有必要对相关系数进行显著性检验，以此来说明建立的回归模型有无实际意义。

为保证回归方程具有最低的线性关系，人们将相关系数r的临界值列成专门的表，即相关系数检验表。在给定的显著性水平α值以及自由度n，查相关系数检验表，即可找到对应的r的最低临界值r_α，据此就可以判断线性关系是否成立。显著性水平α通常取0.05（95%以上建立的回归模型方才可靠、精确）。自由度指的是样本容量n与回归模型中待定参数的个数m之间的差，即自由度=n-m。如例7.3中样本容量n=10，回归模型中待定参数个数m=2，则自由度=n-m=10-2=8。若|r|≥r_α（n-m），表明在显著性水平α条件下，变量间的线性关系是显著的，建立的回归方程是有意义的；若|r|＜r_α（n-m），表明在显著性水平α条件下变量间的线性关系不显著，建立的回归模型实际意义待定。(www.xing528.com)

【例7-4】依据【例7-3】的资料，对某食品企业产品年广告费及年销售收入的相关关系进行显著性检验。

由【例7-1】计算可知，r=0.9340，自由度=n-m=10-2=8，给定α=0.05，查附表10“相关系数检验表”得r_{0.05（10-2）}=0.632。r＞r_{0.05（10-2）}，它表明有95%的概率保证某食品企业产品年广告费与年销售收入之间具有线性相关关系，所建立的回归方程y=48.2143+1.1429x是有意义的。

（2）估计标准误差检验 估计标准误差也称为估计标准差或估计标准误，是残差平方和的算术平均数的平方根，用S_y表示。其计算公式为

式中 S_y——估计标准误差；

e_i——估计残差（实际值与估计值之差）；

n——样本容量；

m——回归模型中待定参数的个数。

残差的平方和可以反映出实际值与回归直线的离散程度。而计算其平均数，可以消除求和项数对残差平方和的影响。因而，在此基础上计算出的估计标准误差更能反映出实际值与回归直线的平均离散程度。估计标准差是一项误差分析指标，用于判断回归模型拟合的优劣程度。

上式计算估计标准差较繁琐，可以采用简捷计算方法估计标准差。其简捷计算公式为

【例7-5】运用表7-5中的数据计算估计标准差。由表7-5可知，=28885，a=48.2143，b=1.1429，=537，n=10，m=2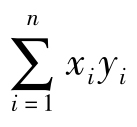，=2616，则用简捷公式计算估计标准差

S_y越大，实际值与回归直线的离散程度越大；反之，S_y越小，实际值与回归直线的离散程度越小。一般要求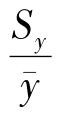＜15%。

运用上述两种公式计算出的估计标准差从理论上说应该是相等的，但在实际计算过程中，由于回归方程的待定系数a和b也是利用公式计算出来的，在计算的过程中通常会涉及到四舍五入的情况，从而导致两种计算公式的结果不一致。但其偏差往往很小，不会影响对问题的分析。

上例中S_y=0.7154，=53.7，=0.0133

由此可见，一元线性回归方程y=48.2143+1.1429x精度较好。

3.运用模型进行预测

一元线性回归模型通过上述检验，若其精度较好，拟合度优，即可用其进行预测。如本节例7-1中一元线性回归方程y=48.2143 +1.1429x，若2005年该企业产品广告费为8万元，将x=8（万元）代入回归方程中，则年销售收入预测值为

y=48.2143+1.1429×8=57.3862（万元）

由于实际计算中不可避免要出现误差，因而预测值应该是在一定的范围之内的一个数值，而不是一个确定值。因此，除了测算一个数值点外，还应测算预测值可能产生的范围，即测算其置信区间。上述预测只测算了一个数值点，假定其他因素不变，S_y=0.7154，置信度为95%（F_（t）=95%），查附录2的正态分布概率表，F_（t）=95%，t=1.96，则该企业产品2005年估计销售收入为

即年广告费为8万元时，其年销售收入在（55.984，58.7918）之间。

【例7-6】某地居民日平均消费水平和食品类销售额统计资料如表7-5第2、3列所示，根据表中资料分析居民平均消费水平与食品类销售额的关系，并预测居民年平均消费水平达到213元时的食品类销售额。

表7-5 某地食品销售额依居民消费水平回归方程计算表

第一，建立回归模型。令居民平均消费水平为x，食品类销售额为。设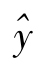=a +b x。

第二，计算参数a和b的值。依据表7-5资料计算可得

由此，可得一元线性回归方程：=4.593+0.7927x。

第三，进行相关性检验。

（1）计算相关系数

可见，与x具有高度线性相关。

（2）估计标准误差检验

由此可判断出与x的线性相关是较强的。

第四，预测当居民平均消费水平达到213元时，食品类销售额是多少。

将x=213（元），代入=4.593+0.7927x，得

若其可靠度为95%，则其置信区间为（173.438-1.96 ×0.9598，173.438 +1.96 ×0.9598）即置信区间为（171.56，175.36），则当下一年食品类销售额的预测范围在171.52～175.32元。