项目二相关分析-试验设计与统计分析

一、相关关系的种类

现象之间的相关关系可以从不同的角度进行分类，不同种类的相关关系需要用不同的方法进行研究。

1.按相关因素的多少分为单相关和复相关

现象之间的相关因素，只涉及到一个自变量和一个因变量之间的依存关系，就称为单相关。如果涉及到三个以上变量之间关系时，即一个因变量与其中两个或多个自变量的复杂依存关系，就称为复相关，或多元相关。在实际中，像施肥量与亩产量，身高与体重，总产量与单位成本等都是单相关。资金周转速度、流通费用、销售量、销售价格与销售利润间的关系即为复相关。从方法上讲，单相关是复相关的基础，在实际工作中，如果存在多个自变量因素，常常都是抓住最主要的因素研究其相关关系。也就是说，可以把多因素的复相关，抓住主要因素化成单相关来加以研究和测定。

2.按相关的形式不同分为直线相关和曲线相关

直线相关又称线性相关，是指两个变量的对应取值在坐标轴上大致呈一条直线。曲线相关指两个变量的对应取值在坐标轴上大致呈一条曲线，如抛物线、双曲线、指数曲线等。

相关关系表现为直线或某一种曲线，这是客观现象本身所固有的，不是由人的主观意识所决定的。现象表现为不同形式的相关关系，就要用不同的统计方法去研究。因此，进行相关分析时，首先要确定相关关系的表现形式。

3.按相关变量变化的方向不同分为正相关和负相关

当一个现象的变量数值增加或减少，另一个现象的变量数值也增加或减少，两个变量的变动方向一致，有同增或同减的关系，称为正相关。如在一定范围内，施肥量增多，亩产量也增多；单位产品原材料消耗量降低，单位成本也随之降低等，都是属于正相关现象。

当一个现象的变量数值增加时，另一个现象的变量数值相应地减少，即两个变量是一增一减或一减一增的关系，称为负相关。如劳动生产率的提高，产品成本降低；商品价格降低，商品的销售量增多等，都是属于负相关现象。

4.按相关的程度分为完全相关、不完全相关和不相关

两个变量之间，当自变量为一定量时，因变量的改变量也随之完全确定，这两个变量之间的关系，称为完全相关。实质上就是确定性的函数关系，也就是说，函数关系是特殊的相关关系。两种现象的变量各自独立，互不影响，就称为不相关。例如，苹果的脆与甜是不相关的。两个现象之间的关系，介于完全相关与不相关之间，称为不完全相关。一般的相关现象都属于这种不完全相关关系。这类相关现象是相关分析的主要研究对象。

二、相关分析的内容

相关分析是对客观现象间存在的相关关系进行分析研究的一种统计方法。其目的在于对现象间所存在的依存关系，以及所表现出的规律性进行数量上的推断和认识，以便做出预测和决策。相关分析的内容包括以下两个方面。

1.判别现象间有无相关关系

现象间有无相关关系，这是相关分析的出发点。只有现象间确实存在相关关系，才可能进行相关分析。所以进行相关分析时，首先要通过定性分析，借助相关表和相关图来判别现象间是否确实存在相关关系，否则就会产生认识上的偏差，得出错误的分析结论。

2.测定相关关系的表现形态和密切程度

相关关系是一种数量上不严格的相互依存关系。只有当变量间确实存在高度密切的相关关系时，才可能进行相关分析，对现象进行预测、推算和决策。因此，判定现象间存在相关关系后，需要进一步测定相关关系的表现形态和密切程度。统计上，一般是通过编制相关表、绘制相关图和计算相关系数来做出判断。

三、相关分析的任务

相关分析的目的，就是要在错综复杂的客观现象中，通过大量观察的统计资料，探讨现象之间相互依存关系的形式和相关的密切程度，找出合适的表达形式，为推算未知和预测未来提供数据，具体任务有以下几方面。

1.揭示现象之间是否具有相关关系

这要从两个方面加以判断：一方面要对现象之间的联系开展理论研究，按照经济理论，专业知识和实践经验，进行定性分析和判断；另一方面要对大量的实际统计资料，通过编制相关表，绘制相关图等一系列统计分析方法，对被研究的现象变量之间是否真正存在相关关系做出统计判断。

2.测定现象相关关系的密切程度

相关关系是一种不严格的数量关系，统计分析的任务之一就是要确定这种数量关系的密切程度，通常是计算相关系数或相关指数，以反映相关关系的密切程度。

3.构建现象相关关系数学模型

依据相关的密切程度，研究确定相关变量之间数量关系的表现形式，确立恰当的数学模型，以便对其进行回归分析。

4.测定因变量估计值的误差程度

根据已确定的变量之间相关的直线方程或曲线方程，在给定若干个自变量值时，可求出因变量相应的估计值。一般来说，估计值与实际值是有一定出入的，相关分析要通过科学方法测定估计值与实际的误差程度，从而确认相关与回归分析的可靠性大小。

四、相关关系的测定

测定现象之间的相关关系有相关系数、相关指数等统计分析指标，下面介绍相关系数及其计算方法。

1.相关系数的概念和特点

相关系数是指在直线相关的条件下，说明两个现象之间相关关系紧密程度的统计分析指标。用r表示。相关系数的取值范围和意义可概括为以下几点，相关系数对应直线相关程度如表7-1所示。(www.xing528.com)

（1）r的取值范围为-1≤r≤1。

（2）r的绝对值越接近1，表明相关关系越密切；越接近0，表明相关关系越不密切。

（3）r=+1或r=-1，表明两个现象完全相关。

（4）r=0，表明两变量无直线相关关系。

（5）r＞0，现象呈正相关；r＜0，现象呈负相关。实践中，一般将现象的相关关系分为四个等级：＜0.3表示微弱相关，0.3≤＜0.5表示低度相关；0.5≤＜0.8表示显著相关；≥0.8表示高度相关。

表7-1 相关系数对应直线相关程度

2.相关系数的特点

（1）两变量为对等关系，可以不区分自变量和因变量，其相关系数只有一个值。

（2）相关系数有正负号，反映正相关或负相关关系。

（3）若以抽样调查取得资料，则两变量均应有相同的随机性，这也是对等关系的要求。对全面统计资料而言，不存在随机性的问题，均为确定性资料。

3.简单相关系数的计算

（1）积差法计算公式

式中，r表示简单相关系数；x表示自变量；y表示因变量；x_i表示自变量及其变量值；y_i表示因变量及其变量值。该公式也可写成

式中，r表示简单相关系数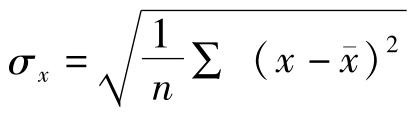；代表自变量的标准差；σ_y=代表因变量的标准差；代表自变量x与因变量y的协方差。由此可知，相关系数是两个变量协方差与两个变量标准差乘积的比。

【例7-1】某食品公司连续10年广告费的投入与每年销售收入的关系，如表7-2所示，请说明广告费的投入与年销售收入的相关情况。

表7-2 某食品公司广告费与销售收入

利用表7-2的统计资料计算简单相关系数。

先计算年广告费x的平均数和年销售收入y的平均数y-

再将表7-3中的数据代入积差法公式得

相关系数r=0.9340，说明A产品年广告费用与年销售收入之间的关系是高度相关关系。

表7-3 积差法相关系数计算表

续表

（2）简捷法

简捷法相关系数计算表如表7-4所示。

表7-4 简捷法相关系数计算表

根据积差法计算简单相关系数比较麻烦，计算项目较多，会导致相关系数的数值出现一定程度的误差。将积差法公式整理变形，得出相关系数的简捷计算公式

【例7-2】根据【例7-1】表中数据，利用表3用简捷法计算简单相关系数

利用简捷算法计算的结果与积差法计算的结果基本相同，但简捷算法少计算了一部分数值，提高了计算效率，也就相应提高了相关系数的准确性。

（3）其他变形公式

利用相关系数积差法公式可推导出相关系数的其他计算公式