项目四双因素试验方差分析的结果

一、双因素试验概述

在许多实际问题中，往往要同时考虑两个因素对试验指标的影响。例如，进行某一项试验，当影响指标的因素不是一个而是多个时，要分析各因素的作用是否显著，就要用到多因素的方差分析。当有两个因素时，除每个因素的影响之外，还有这两个因素的搭配问题。如图6-2中的两组试验结果，都有两个因素A和B，每个因素取两个水平。

图6-2

图6-2（1）中，无论B在什么水平（B₁还是B₂），水平A₂下的结果总比A₁下的高20；同样地，无论A是什么水平，B₂下的结果总比B₁下的高40。这说明A和B单独地各自影响结果，互相之间没有作用。

图6-2（2）中，当B为B₁时，A₂下的结果比A₁的高，而且当B为B₂时，A₁下的结果比A₂的高；类似地，当A为A₁时，B₂下的结果比B₁的高70，而A为A₂时，B₂下的结果比B₁的高30。这表明A的作用与B所取的水平有关，而B的作用也与A所取的水平有关。即A和B不仅各自对结果有影响，而且它们的搭配方式也有影响。把这种影响称作因素A和B的交互作用，记作A×B在双因素试验的方差分析中，不仅要检验水平A和B的作用，还要检验它们的交互作用。

二、等重复的双因素试验方差分析

设有两个因素A，B作用于试验的指标，因素A有r个水平A₁，A₂，…，Ar，因素B有s个水平B₁，B₂，…，B_s，现对因素A，B的水平的每对组合（A_i，B_j），i=1，2，…，r；j=1，2，…，s都作t（t≥2）次试验（称为等重复试验），得到如表6-16的结果。

表6-16 等重复的双因素试验

设x_ijk～N（μ_ij，σ²），i=1，2，…，r；j=1，2，…，s；k=1，2，…，t，各x_ijk独立，这里μ_ij，σ²均为未知参数，或写为

记

于是

称μ为总平均，α_i为水平A_i的效应，β_j为水平B_j的效应，γ_ij为水平A_i和水平B_j的交互效应，这是由A_i，B_j搭配起来联合作用而引起的。可知

这样式6-40可写成

其中μ，α_i，β_j，γ_{i j}及σ²都为未知参数。

式6-42就是所要研究的双因素试验方差分析的数学模型。要检验因素A，B及交互作用A×B是否显著，要检验以下3个假设：

类似于单因素情况，对这些问题的检验方法也是建立在平方和分解上的。记作

不难验证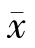，，，分别是μ，μ_i·，μ·_j，μ_ij的无偏估计。

由，1≤i≤r，1≤j≤s，1≤k≤t，得平方和的分解式，如式6-43所示。

其中

S_E称为误差平方和，S_A，S_B分别称为因素A，B的效应平方和，S_A×B称为A，B交互效应平方和。

当H₀₁：α₁=α₂=…=α_r=0为真时，

当假设H₀₂为真时，

当假设H₀₃为真时，

当给定显著性水平α后，假设H₀₁，H₀₂，H₀₃的拒绝域分别为

经过上面的分析和计算，可得出双因素试验的方差分析，如表6-17所示。

表6-17 双因素试验的方差分析表

在实际中，与单因素方差分析类似，可按以下较简便的公式来计算S_T，S_A，S_B，S_A×B，S_E。

记

即有(www.xing528.com)

【例6-4】为探讨某食品化学反应中温度和催化剂对收率的影响，实验员选了三种温度（A）和三种不同的催化剂（B），观察数据如表6-18所示。试在显著水平0.10下分析不同的温度（A），催化剂（B）以及它们的交互作用（A×B）对收率有无显著影响。

表6-18 温度和催化剂对收率的影响

根据题意，需检验假设H₀₁，H₀₂，H₀₃。r=s=3，t=2，T_···，T_ij·，T_i··，T_·j·的计算如表6-19所示。

表6-19 【例6-4】的计算结果

得方差分析表如6-20所示。

表6-20 例6-4的方差分析表

由于F_0.10（2，9）=3.01＞F_A，F_0.10（2，9）＞F_B，F_0.10（4，9）=2.69＞F_A×B，因而接受假设H₀₁，H₀₂，H₀₃，即温度、催化剂以及它们的交互作用对化学反应的收率的影响不显著。

三、无重复的双因素试验方差分析

在双因素试验中，如果对每一对水平的组合（A_i，B_j）只做一次试验，即不重复试验，所得结果如表6-21所示。

表6-21 无重复双因素试验

这时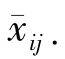=x_ijk，S_E=0，S_E的自由度为0，故不能利用双因素等重复试验中的公式进行方差分析。但如果认为A，B两因素无交互作用，或已知交互作用对试验指标影响很小，则可将S_A×B取作S_E，仍可利用等重复的双因素试验对因素A，B进行方差分析。对这种情况下的数学模型及统计分析表示如下所示。

由式6-42可得到，

要检验的假设有以下两个：

记

平方和分解公式为

其中

分别为总平方和、因素A，B的效应平方和及误差平方和。

取显著性水平为α，当H₀₁成立时，

H₀₁拒绝域为

当H₀₂成立时

H₀₂拒绝域为

得方差分析如表6-22所示。

表6-22 无重复双因素试验方差分析表

【例6-5】测试品牌白酒在不同酒精含量和各种温度下的挥发值，表6-23列出了试验的数据，问试验温度、酒精含量对白酒的挥发值的影响是否显著？（α=0.01）

表6-23 品牌白酒在不同酒精含量和各种温度下的挥发试验

解：已知r=4，s=3，需检验假设H₀₁，H₀₂，经计算得方差分析如表6-24所示。

表6-24 例6-5的方差分析表

由于F_0.01（3，6）=9.78＜F_A，拒绝H₀₁。F_0.01（2，6）=10.92＜F_B，拒绝H₀₂。检验结果表明，试验温度、酒精含量对白酒的挥发值影响是显著的。