项目三单因素试验方差分析结果

一、单因素试验介绍

在试验中，将要考查的指标称为试验指标，影响试验指标的条件称为因素。因素可分为两类，一类是人们可以控制的；一类是人们不能控制的。例如，原料成分、反应温度、溶液浓度等是可以控制的，而测量误差、气象条件等一般是难以控制的。以下所说的因素都是可控因素，因素所处的状态称为该因素的水平。在方差分析中，根据所研究试验因素的多少，可分为单因素、双因素和多因素试验资料的方差分析。单因素试验资料的方差分析是其中最简单的一种，目的在于正确判断该试验因素各水平的优劣。根据各处理内重复数是否相等，单因素方差分析又分为重复数相等和重复数不等两种情况。

二、各处理重复数相等的方差分析

【例6-2】抽测5个不同品种的若干头母猪的窝产仔数，结果如表6-8所示，试检验不同品种母猪平均窝产仔数的差异是否显著。

表6-8 五个不同品种母猪的窝产仔数

这是一个单因素试验，k=5，n=5。现对此试验结果进行方差分析如下所述。

（1）计算各项平方和与自由度

（2）列出方差分析表，进行F检验，如表6-9所示。

表6-9 不同品种母猪的窝产仔数的方差分析表

根据df₁=df_t=4，df₂=df_e=20查临界F值得：F_{0.05（4，20）}=2.87，F_{0.01（4，20）}=4.43，因为F＞F_{0.01（4，20）}，即P＜0.01，表明品种间产仔数的差异极显著。

（3）多重比较 采用新复极差法，各处理平均数多重比较，如表6-10所示。

表6-10 不同品种母猪的平均窝产仔数多重比较表（SSR法）

因为MS_e=3.14，n=5，所以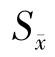为

根据df_e=20，秩次距k=2，3，4，5，由附录8查出α=0.05和α=0.01的各临界SSR值，乘以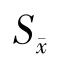=0.7925，即得各最小显著极差，所得结果如表6-11所示。

表6-11 SSR值及LSR值

将表6-10中的差数与表6-11中相应的最小显著极差比较，结果表明：5号品种母猪的平均窝产仔数极显著高于2号品种母猪，显著高于4号和1号品种，但与3号品种差异不显著；3号品种母猪的平均窝产仔数极显著高于2号品种，与1号和4号品种差异不显著；1号、4号、2号品种母猪的平均窝产仔数间差异均不显著。五个品种中以5号品种母猪的窝产仔数最高，3号品种次之，2号品种母猪的窝产仔数最低。

三、各处理重复数不等的方差分析(www.xing528.com)

在各处理重复数不等的情况下，方差分析步骤与各处理重复数相等的情况相同，只是在有关计算公式上略有差异。

设处理数为k；各处理重复数为n₁，n₂，…，n_k；试验观测值总数为N=∑n_i，则

【例6-3】5个不同品种牛的育肥试验，后期15d增重质量（kg），如表6-12所示。试比较品种间增重有无差异。

表6-12 5个品种牛30d增重质量

此例处理数k=5，各处理重复数不等。现对此试验结果进行方差分析如下：

（1）计算各项平方和与自由度

利用式（6-37）计算得

（2）列出方差分析表，进行F检验 临界F值为：F_{0.05（4，20）}=2.87，F_{0.01（4，20）}=4.43，因为品种间的F值5.99＞F_{0.01（4，20）}，P＜0.01，表明品种间差异极显著，如表6-13所示。

表6-13 5个品种育肥牛增重方差分析表

（3）进行多重比较 采用新复极差法，各处理平均数多重比较，如表6-14所示。因为各处理重复数不等，应先由式（6-37）计算出平均重复次数n₀来代替标准误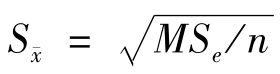中的n，此例

于是，标准误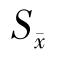

表6-14 5个品种育肥牛平均增重多重比较表（SSR法）

根据df_e=20，秩次距k=2，3，4，5，从附表8中查出α=0.05与α=0.01的临界SSR值，乘以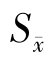=0.63，即得各最小显极差，所得结果如表6-15所示。

表6-15 SSR值及LSR值表

将表6-14中的各个差数与表6-15中相应的最小显著极差比较，多重比较结果表明，B₁、B₄品种的平均增重极显著或显著高于B₂、B₅品种的平均增重，其余不同品种之间差异不显著。可以认为B₁、B₄品种增重最快，B₂、B₅品种增重较差，B₃品种居中。

单因素试验只能解决一个因素各水平之间的比较问题。如上述研究几个品种牛的育肥试验，只能比较几个品种的增重快慢。而影响增重的其他因素，如饲料中能量的高低、蛋白质含量的多少、饲喂方式及环境温度的变化等就无法得以研究。实际上，往往对这些因素有必要同时考查，只有这样才能做出更加符合客观实际的科学结论，才有更大的应用价值。这就要求进行双因素或多因素试验。下面介绍双因素试验资料的方差分析法。