多重比较方法及统计推断

F值显著或极显著，否定了无效假设H₀，表明试验的总变异主要来源于处理间的变异，试验中各处理平均数间存在显著或极显著差异，并不意味着每两个处理平均数间的差异都显著或极显著，也不能具体说明哪些处理平均数间有显著或极显著差异，哪些差异不显著。因而，有必要进行两两处理平均数间的比较，以具体判断两两处理平均数间的差异是否显著。统计上把多个平均数两两间的相互比较称为多重比较（multiple comparisons）。多重比较的方法有很多，常用的有最小显著差数法（LSD法）和最小显著极差法（LSR法），现分别介绍如下。

一、最小显著差数法

最小显著差数法简称LSD法（least significant difference），该方法的基本原理是：在F检验显著的前提下，先计算出显著水平为α的最小显著差数LSD_α，然后将任意两个处理平均数的差数的绝对值与其进行比较。若＞LSD_a，则与在α水平上差异显著；反之，在α水平上差异不显著。最小显著差数计算公式如下：

式中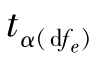：为在F检验中误差自由度下，显著水平为α的临界t值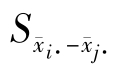，为均数差异标准误，计算公式如下：

其中，MS_e为F检验中的误差均方，n为各处理的重复数。

当显著水平α=0.05和0.01时，从t值表中查出和，代入式6-28得公式如下：

利用LSD法进行多重比较时，可按如下步骤进行。

（1）列出平均数的多重比较表，比较表中各处理按其平均数从大到小自上而下排列。

（2）计算最小显著差数LSD_0.05和LSD_0.01。

（3）将平均数多重比较表中两两平均数的差数与LSD_0.05、LSD_0.01比较，做出统计推断。

对于【例6-1】，各处理的多重比较如表6-4所示。

表6-4 四种饲料平均增重的多重比较表（LSD法）

注：表中A₄与A₃的差数为3.22，用q检验法时，在α=0.05的水平上不显著。

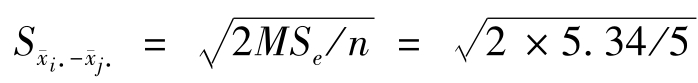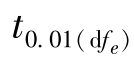因为，=1.462；查t值表得：=t_0.05（16）=2.120，=t_0.01（16）=2.921。

所以，显著水平为0.05与0.01的最小显著差数：

将表6-4中的6个差数与LSD_0.05，LSD_0.05比较：小于LSD_0.05者不显著，在差数的右上方标记“ns”，或不标记符号；介于LSD_0.05与LSD_0.01之间者显著，在差数的右上方标记“*”；大于LSD_0.01者极显著，在差数的右上方标记“**”。检验结果除差数1.68、1.54不显著、3.22显著外，其余两个差数6.44、4.90极显著。表明A₁饲料对鸡的增重效果极显著高于A₂和A₃，显著高于A₄；A₄饲料对鸡的增重效果极显著高于A₃饲料；A₄与A₂、A₂与A₃的增重效果差异不显著，以A₁饲料对鸡的增重效果最佳。

二、最小显著极差法

简称LSR法（Least significant ranges），LSR法的特点是把平均数的差数看成是平均数的极差，根据极差范围内所包含的处理数（称为秩次距）k的不同而采用不同的检验尺度，以克服LSR法的不足。这些在显著水平α上，依秩次距k的不同而采用的不同的检验尺度叫做最小显著极差LSR。例如，有10个要相互比较，先将10个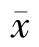依其数值大小顺次排列，两极端平均数的差数（极差）的显著性，由其差数是否大于秩次距k=10时的最小显著极差决定（≥为显著，＜为不显著；而后是秩次距k=9的平均数的极差的显著性，则由极差是否大于k=9时的最小显著极差决定；直到任何两个相邻平均数的差数的显著性由这些差数是否大于秩次距k=2时的最小显著极差决定为止。因此，有k个平均数相互比较，就有k-1种秩次距（k，k-1，k-2，…，2），因而需求得k-1个最小显著极差（LSR_α，k），分别作为判断具有相应秩次距的平均数的极差是否显著的标准。

因为LSR法是一种极差检验法，所以当一个平均数大集合的极差不显著时，其中所包含的各个较小集合极差也应一概作不显著处理。

LSR法克服了LSR法的不足，但检验的工作量有所增加。常用的LSR法有q检验法和新复极差法两种。

1.q检验法（qtest）

此法是以统计量q的概率分布为基础的。q值由下式求得

式中，ω为极差，为标准误，q分布依赖于误差自由度df_e及秩次距k。利用q检验法进行多重比较时，为了简便起见，不是将由式6-31算出的q值与临界q值比较，而是将极差与比较，从而做出统计推断。即为α水平上的最小显著极差。

当显著水平α=0.05和0.01时，从附表7（q值表）中根据自由度df_e及秩次距k查出和代入式6-33得

实际利用q检验法进行多重比较时，可按如下步骤进行。

（1）列出平均数多重比较表。

（2）由自由度df_e、秩次距k查临界q值，计算最小显著极差LSR_0.05，k，LSR_0.01，k。

（3）将平均数多重比较表中的各极差与相应的最小显著极差LSR_0.05，k，LSR_0.01，k比较，做出统计推断。

对于【例6-1】，各处理平均数多重比较如表6-4所示。其中，极差1.54、1.68、3.22的秩次距为2；极差3.22、4.90的秩次距为3；极差6.44的秩次距为4。

因为，MS_e=5.34，故标准误为

根据df_e=16，k=2，3，4由附表7查出α=0.05、0.01水平下临界q值，乘以标准误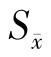求得各最小显著极差，所得结果如表6-5所示。(www.xing528.com)

表6-5 q值及LSR值

将表6-4中的极差1.54、1.68、3.22与表6-5中的最小显著极差3.099、4.266比较；将极差3.22、4.90与3.770、4.948比较；将极差6.44与4.184、5.361比较。检验结果，除A₄与A₃的差数3.22由LSD法比较时的差异显著变为差异不显著外，其余检验结果同LSD法。

2.新复极差法（new multiple range method）

此法是由邓肯（Duncan）于1955年提出，故又称Duncan法，此法还称SSR法（shortest significant ranges）。

新复极差法与q检验法的检验步骤相同，唯一不同的是计算最小显著极差时需查SSR表（附录8）而不是查q值表。最小显著极差计算公式为

其中是根据显著水平α、误差自由度df_e、秩次距k，由SSR表查得的临界SSR值，。α=0.05和α=0.01水平下的最小显著极差为

对于【例6-1】，已算出=1.033，依df_e=16，k=2，3，4，由附录8查临界SSR_{0.05（16，k）}和SSR_{0.01（16，k）}值，乘以=1.033，求得各最小显著极差，所得结果如表6-6所示。

表6-6 SSR值与LSR值

将表6-4中的平均数差数（极差）与表6-6中的最小显著极差比较，检验结果与q检验法相同。

当各处理重复数不等时，为了简便起见，不论LSD法还是LSR法，可如式6-36所示计算出一个各处理平均的重复数n₀，以代替计算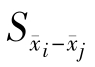或所需的n。

式中 k为试验的处理数，n_i（i=1，2，…，k）为第i处理的重复数。

以上介绍的三种多重比较方法，其检验尺度有如下关系：

LSD法≤新复极差法≤q检验法

当秩次距k=2时，取等号；秩次距k≥3时，取小于号。在多重比较中，LSD法的尺度最小，q检验法尺度最大，新复极差法尺度居中。根据上述排列顺序，前面方法检验显著的差数，用后面方法检验未必显著；用后面方法检验显著的差数，用前面方法检验必然显著。一个试验资料究竟采用哪一种多重比较方法，主要应根据否定一个正确的H₀和接受一个不正确的H₀的相对重要性来决定。如果否定正确的H₀是事关重大或后果严重的，或对试验要求严格时，用q检验法较为妥当；如果接受一个不正确的H₀是事关重大或后果严重的，则宜用新复极差法。生物试验中，由于试验误差较大，常采用新复极差法；F检验显著后，为了简便，也可采用LSD法。

三、多重比较结果的表示法

各平均数经多重比较后，应以简明的形式将结果表示出来，常用的有以下两种方式。

1.三角形法

此法是将多重比较结果直接标记在平均数多重比较表上，如表6-4所示。由于在多重比较表中各个平均数差数构成一个三角形阵列，故称为三角形法。此法的优点是简便直观，缺点是占的篇幅较大。

2.标记字母法

此法是先将各处理平均数由大到小、自上而下排列，然后在最大平均数后标记字母a，并将该平均数与以下各平均数依次相比，凡差异不显著标记同一字母a，直到某一个与其差异显著的平均数标记字母b；再以标有字母b的平均数为标准，与上方比它大的各个平均数比较，凡差异不显著一律再加标b，直至显著为止；再以标记有字母b的最大平均数为标准，与下面各未标记字母的平均数相比，凡差异不显著，继续标记字母b，直至某一个与其差异显著的平均数标记c，……如此重复下去，直至最小一个平均数被标记比较完毕为止。这样，各平均数间凡有一个相同字母的即为差异不显著，凡无相同字母的即为差异显著。用小写拉丁字母表示显著水平α=0.05，用大写拉丁字母表示显著水平α=0.01。在利用字母标记法表示多重比较结果时，常在三角形法的基础上进行。此法的优点是占篇幅小，在科技文献中常见。

对于【例6-1】，现根据表6-4所表示的多重比较结果用字母标记如表6-7所示（用新复极差法检验，表6-4中A₄与A₃的差数3.22在α=0.05的水平上不显著，其余的与LSD法同）。

表6-7 多重比较结果的字母标记（SSR法）

在表6-7中，先将各处理平均数由大到小、自上而下排列。当显著水平α=0.05时，先在平均数31.18行上标记字母a；由于31.18与27.96之差为3.22，在α=0.05水平上显著，所以在平均数27.96行上标记字母b；然后以标记字母b的平均数27.96与其下方的平均数26.28比较，差数为1.68，在α=0.05水平上不显著，所以在平均数26.28行上标记字母b；再将平均数27.96与平均数24.74比较，差数为3.22，在α=0.05水平上不显著，所以在平均数24.74行上标记字母b。类似地，可以在α=0.01将各处理平均数标记上字母，结果如表6-7所示。q检验结果与SSR法检验结果相同。

由表6-7可以发现，A₁饲料对鸡的平均增重极显著地高于A₂和A₃饲料，显著高于A₄饲料；A₄、A₂、A₃三种饲料对鸡的平均增重差异不显著。四种饲料其中以A₁饲料对鸡的增重效果最好。

应当注意，无论采用哪种方法表示多重比较结果，都应注明采用的是哪一种多重比较法。

四、方差分析的基本步骤

根据任务一和任务二的介绍，方差分析的基本步骤现归纳如下所述。

（1）计算各项平方和与自由度。

（2）列出方差分析表，进行F检验。

（3）若F检验显著，则进行多重比较。多重比较的方法有最小显著差数法（LSD法）和最小显著极差法（LSR法：包括q检验法和新复极差法）。表示多重比较结果的方法有三角形法和标记字母法。