多平均数差异显著性检验需用方差分析法，其原因和应用

t检验法适用于样本平均数、总体平均数及两样本平均数间的差异显著性检验，但在生产和科学研究中经常会遇到比较多个处理优劣的问题，即需要进行多个平均数间的差异显著性检验，这时不适宜采用t检验法，原因如下所述。

（1）检验过程烦琐 例如，一个试验包含5个处理，采用t检验法要进行=10次两两平均数的差异显著性检验；若有k个处理，则要作k（k-1）/2次类似的检验。因此，整个检验过程非常复杂，烦琐。

（2）无统一的试验误差，误差估计的精确性和检验的灵敏性低 对同一试验的多个处理进行比较时，应该有一个统一的试验误差估计值。若用t检验法作两两比较，由于每次比较需计算一个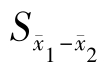，故使得各次比较误差的估计不统一，同时没有充分利用资料所提供的信息而使误差估计的精确性降低，从而降低检验的灵敏性。例如，试验有5个处理，每个处理重复6次，共有30个观测值。进行t检验时，每次只能利用两个处理共12个观测值估计试验误差，误差自由度为2 ×（6-1）=10；若利用整个试验的30个观测值估计试验误差，显然估计的精确性高，且误差自由度为5 ×（6-1）=25。可见，在用t检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。

（3）推断的可靠性低，检验的错误率大 即使利用资料所提供的全部信息估计了试验误差，若用t检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大错误的概率，降低推断的可靠性。

由于上述原因，多个平均数的差异显著性检验不宜采用t检验，须采用方差分析法。

方差分析（analysis of variance）是由英国统计学家费雪（R. A. Fisher）于1923年提出的。这种方法是将k个处理的观测值作为一个整体看待，把观测值总变异的平方及自由度分解为相应的不同变异来源的平方及自由度，进而获得不同变异来源的总体方差的估计值。通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。方差分析实质上是关于观测值变异原因的数量分析，它在科学研究中应用十分广泛。

方差分析有很多类型，其数学模型的具体表达式也有所不同，但以下三点却是共同的，是进行方差分析的基本前提或基本假定。

（1）效应的可加性 进行方差分析的模型均为线性可加模型。这个模型明确提出了处理效应与误差效应是“可加的”，正是由于这一“可加性”，才有了样本平方和的“可加性”，亦即有了试验观测值总平方和的“可剖分”性。如果试验资料不具备这一性质，那么依据变异原因去剖分变量的总变异将失去根据，方差分析不能正确进行。

（2）分布的正态性 是指所有试验误差是相互独立的，且都服从正态分布N（0，σ²）。只有在这样的条件下才能进行F检验。

（3）方差的同质性 即各个处理观测值总体方差σ²应是相等的。只有这样，才有理由以各个处理均方的合并均方作为检验各处理差异显著性的共同的误差均方。

一、线性模型与基本假定

假设某单因素试验有k个处理，每个处理有n次重复，共有nk个观测值。这类试验资料的数据模式如表6-1所示。

表6-1 k个处理每个处理有n个观测值的数据模式

其中x_ij表示第i个处理的第j个观测值（i=1，2，…，k；j=1，2，…，n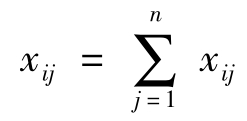）；表示第i个处理n个观测值的和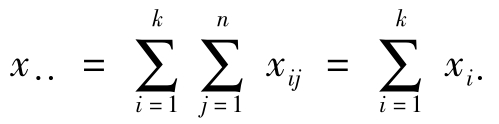；表示全部观测值的总和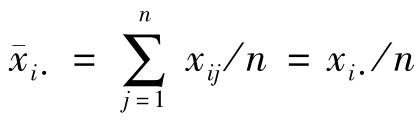；表示第i个处理的平均数；=x_··/n表示全部观测值的总平均数；x_ij可以分解为

μ_i表示第i个处理观测值总体的平均数。为了看出各处理的影响大小，将μ_i再进行分解，令

则

其中μ表示全试验观测值总体的平均数，α_i是第i个处理的效应（treatment effects），表示处理i对试验结果产生的影响，显然有

ε_ij是试验误差，相互独立，且服从正态分布N（0，σ²）。

式6-4为单因素试验的线性模型（linear model），亦称数学模型。在这个模型中，x_ij表示总平均数μ、处理效应α_i和试验误差ε_ij之和。由于ε_ij相互独立且服从正态分布N（0，σ²），可知各处理A_i（i=1，2，…，k）所属总体亦应具正态性，即服从正态分布N（μ_i，σ²）。尽管各总体的均数μ_i可以不等或相等，σ²则必须是相等的。所以，单因素试验的数学模型可归纳为：效应的可加性（additivity）、分布的正态性（normality）、方差的同质性（homogeneity）。这也是进行其他类型方差分析的前提或基本假定。

若将表6-1中的观测值x_ij（i=1，2，…，k；j=1，2，…，n）的数据结构（模型）用样本符号来表示，则

与式6-4比较可知，=e_ij分别是μ、（μ_i-μ）=α_i、（x_ij-μ_i）=ε_ij的估计值。

式6-4、式6-6表明：每个观测值都包含处理效应（μ_i-μ或），与误差（x_ij-μ_i或x_ij-x-_i·），故kn个观测值的总变异可分解为处理间的变异和处理内的变异两部分。

二、平方和与自由度的剖分

方差与标准差都可以用来度量样本的变异程度。因为方差在统计分析上有许多优点，而且不用开方，所以在方差分析中是用样本方差即均方（mean squares）来度量资料的变异程度。表6-1中全部观测值的总变异可以用总均方来度量。将总变异分解为处理间变异和处理内变异，就是要将总均方分解为处理间均方和处理内均方。但这种分解是通过将总均方的分子——称为总离均差平方和，简称为总平方和，剖分成处理间平方和与处理内平方和两部分；将总均方的分母——称为总自由度，剖分成处理间自由度与处理内自由度两部分来实现的。

1.总平方和的剖分

如表6-1所示，反映全部观测值总变异的总平方和是各观测值x_ij与总平均数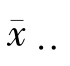的离均差平方和，记为SS_T，即

因为

其中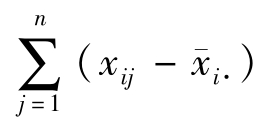=0

所以

式6-8中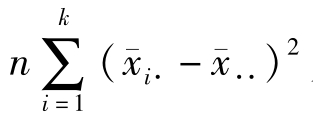，为各处理平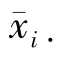均数与总平均数的离均差平方和与重复数n的乘积，反映了重复n次的处理间变异，称为处理间平方和，记为SS_t，

即

式6-8中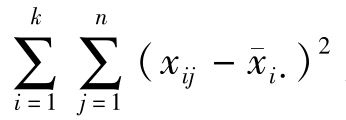，为各处理内离均差平方和之和，反映了各处理内的变异误差，称为处理内平方和或误差平方和，记为SS_e，即

于是有

式6-8、式6-11是单因素试验结果总平方和、处理间平方和、处理内平方和的关系式。这个关系式中三种平方和的简便计算公式为

其中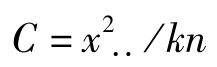，称为矫正数。

2.总自由度的剖分

在平方和计算公式中可以看出，在同样误差程度下，试验数据越多，计算出的平方和越大，因此仅用平方和来反映试验值之间差异的大小还是不够的，还需要试验次数的多少对平方和带来的影响，维持需要考虑自由度（degree of free-dom）。三种平方和对应的自由度分别如下：

SS_T的自由度称为总自由度，即

SS_t的自由度称为处理间自由度，即

SS_e的自由度称为处理内自由度，即

因为

nk-1=（k-1）+（nk-k）=（k-1）+k（n-1）(www.xing528.com)

所以

综合以上各式得

各部分平方和除以各自的自由度便得到总均方、处理间均方和处理内均方，分别记为（MS_T或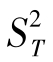）、MS_t（或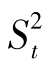）和MS_e（或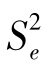），即

总均方一般不等于处理间均方加处理内均方。

【例6-1】某高校畜牧实验室为了比较四种不同配合饲料对鸡的饲喂效果，选取了条件基本相同的20只，随机分成四组，投喂不同饲料，经一个月试验以后，各组鸡的增重结果如表6-2所示。

表6-2 饲喂不同饲料的鸡的增重 单位：g

这是一个单因素试验，处理数k=4，重复数n=5。各项平方和及自由度计算如下。

矫正数

总平方和

处理间平方和

处理内平方和

SS_e=SS_T-SS_t=19966.8-11426.8=8540

总自由度

df_T=nk-1=5×4-1=19

处理间自由度

df_t=k-1=4-1=3

处理内自由度

df_e=df_T-df_t=19-3=16

用SS_t、SS_e分别除以df_t和df_e得到处理间均方MS_t及处理内均方MS_e，即

因为方差分析中不涉及总均方的数值，所以不必计算。

三、F分布与F检验

1.F分布

设想作这样的抽样试验，即在一正态总体N（μ，σ²）中随机抽取样本含量为n的样本k个，将各样本观测值整理成表6-1的形式。此时所谓的各处理没有真实差异，各处理只是随机分的组。因此，由式6-22至式6-24算出的和都是误差方差σ²的估计量。以为分母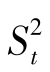，为分子，求其比值。统计学上把两个均方之比值称为F值，即

F值具有两个自由度：df₁=df_t=k-1，df₂=df_e=k（n-1）。

若在给定的k和n的条件下，继续从该总体进行一系列抽样，则可获得一系列的F值。这些F值所具有的概率分布称为F分布（Fdistribution）。F分布密度曲线是随自由度df₁、df₂的变化而变化的一簇偏态曲线，其形态随着df₁、df₂的增大逐渐趋于对称，如图6-1所示。

图6-1 F分布密度曲线

F分布的取值范围是（0，+∞），其平均值μ_F=1。

用f（F）表示F分布的概率密度函数，则其分布函数F（F_a）为

因而，F分布右尾从F_a到+∞的概率为

附表4列出的是不同df₁和df₂下，P（F ≥F_a）=0.05和P（F ≥F_a）=0.01时的F值，即右尾概率α=0.05和α=0.01时的临界F值，一般记作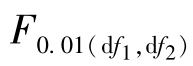，。当df₁=3，df₂=18时，查附表4可知，F_{0.05（3，18）}=3.16，F_{0.01（3，18）}=5.09，表示如以df₁=df_t=3，df₂=df_e=18在同一正态总体中连续抽样，则所得F值大于3.16的仅为5%，而大于5.09的仅为1%。

2.F检验

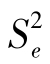附录4是专门为检验代表的总体方差是否比代表的总体方差大而设计的。若实际计算的F值大于，则F值在α=0.05的水平上显著，以95%的可靠性（即冒5%的风险）推断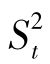代表的总体方差大于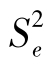代表的总体方差。这种用F值出现概率的大小推断两个总体方差是否相等的方法称为F检验（F-test）。

在方差分析中进行F检验的目的在于推断处理间的差异是否存在，检验某项变异因素的效应方差是否为零。因此，在计算F值时总是以被检验因素的均方作分子，以误差均方作分母。应当注意，分母项的正确选择是由方差分析的模型和各项变异原因的期望均方决定的。

在单因素试验结果的方差分析中，无效假设为H₀：μ₁=μ₂=…=μ_k，备择假设为H_A：各μ_i不全相等，或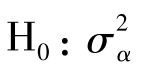=0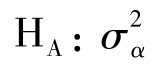，≠0；F=MS_t/MS_e，也就是要判断处理间均方是否显著大于处理内（误差）均方。如果结论是肯定的，我们将否定H₀；反之，不否定H₀。反过来理解：如果H₀是正确的，那么MS_t与MS_e都是总体误差σ²的估计值，理论上讲F值等于1；如果H₀是不正确的，那么MS_t之期望均方中的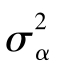就不等于零，F值就必大于1。但是由于抽样的原因，即使H₀正确，F值也会出现大于1的情况。所以，只有F值达到一定程度时，才有理由否定H₀。

实际进行F检验时，是将由试验资料所算得的F值与根据df₁=df_t（大均方，即分子均方的自由度）、df₂=df_e（小均方，即分母均方的自由度）查附录4所得的临界F值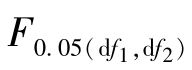，相比较做出统计推断的。

若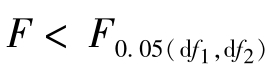，即P＞0.05，不能否定H₀，统计学上把这一检验结果表述为：各处理间差异不显著，在F值的右上方标记“ns”，或不标记符号；若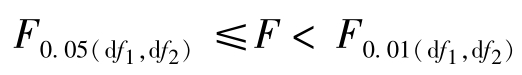，即0.01＜P≤0.05，否定H₀，接受H_A，统计学上把这一检验结果表述为：各处理间差异显著，在F值的右上方标记“*”；若F≥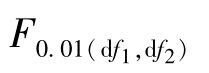，即P≤0.01，否定H₀，接受H_A，统计学上把这一检验结果表述为：各处理间差异极显著，在F值的右上方标记“**”。

对于【例6-1】，因为F=MS_t/MS_e=38.09/5.34=7.13^**；根据df₁=df_t=3，df₂=df_e=16，查附表4，得F＞F_{0.01（3，16）}=5.29，P＜0.01，表明四种不同饲料对鸡的增重效果差异极显著，用不同的饲料饲喂，增重是不同的。

在方差分析中，通常将变异来源、平方和、自由度、均方和F值归纳成一张方差分析表，如表6-3所示。

表6-3 资料方差分析表

表中的F值应与相应的被检验因素齐行。因为经F检验差异极显著，故在F值7.13右上方标记“**”。

在实际进行方差分析时，只须计算出各项平方和与自由度，各项均方的计算及F值检验可在方差分析表上进行。