项目二样本平均数的假设检验：试验设计与统计分析

一、单样本平均数的假设检验

单个样本平均数的假设检验是检验某一样本平均数x-与已知总体平均数μ₀是否有显著差异的方法，即是检验无效假设H₀：μ=μ₀或μ≤μ₀（μ≥μ₀）对备择假设H_A：μ≠μ₀或μ＞μ₀（μ＜μ₀）的问题。具体方法有μ检验和t检验两种。

1.单个样本平均数的μ检验

μ检验（μ-test）方法，就是在假设检验中利用标准正态分布来进行统计量的概率计算的检验方法。以下两种情况的资料可以用μ检验方法分析：①样本资料所属总体服从正态分布N（μ，σ²），总体方差σ²为已知；②样本平均数来自一个大样本（通常n＞120）。下面以实例说明μ检验的具体方法步骤。

【例5-3】某罐头厂生产水果罐头，其自动装罐机在正常工作状态时每罐净重具正态分布N（500，64）（单位为g）。某日随机抽查了10听罐头，测定结果如下（单位：g）：

505，512，497，493，508，515，502，495，490，510。

问灌装机该日工作是否正常？

由题意可知，样本所属总体服从正态分布，并且总体标准差σ=8，符合μ检验的应用条件。由于当日灌装机的每灌平均净重可能高于或低于正常工作状态下的标准净重，故需作两尾检验，其方法步骤如下所述。

（1）提出假设

H₀：μ=μ₀=500g，即该日装罐机平均净重与标准净重一样。

H_A：μ≠μ₀，即该日装罐机平均净重与标准净重不一样，装罐机工作不正常。

（2）确定显著水平α=0.05（两尾概率）。

（3）检验计算

样本平均数

均数标准误

统计量μ量

（4）统计推断 由显著水平α=0.05查附表2得临界μ值：μ_0.05=1.96。

由于实得=1.067＜μ_0.05=1.96，可知表面效应=502.7-500=2.7仅由误差造成的概率p＞0.05，故不能否定H₀，推断该日装罐平均净重与标准净重差异不显著，表明该日灌装机工作属正常状态。

2.单个样本平均数的t检验

t检验（t-test）是利用t分布来进行统计量的概率计算的假设检验方法。它要求资料必须服从正态分布，主要应用于总体方差σ²未知的小样本资料，当然大样本也可用。其他方法步骤由下面的例子进行说明。

【例5-4】用山楂加工果冻，传统工艺平均每100g山楂出果冻500g。现采用一种新工艺进行加工，测定了16次，得每100g山楂出果冻平均数为=520g，标准差S=12g。问新工艺每100g山楂出果冻量与传统工艺有无显著差异？

本例中总体方差σ²未知，又是小样本，资料也服从正态分布，故可作t检验。检验步骤如下所述。

（1）建立假设

H₀：μ=μ₀=500g，即新、旧工艺每100g山楂出果冻没有差异。

H_A：μ≠μ₀，即新、旧工艺每100g山楂出果冻量有差异。

（2）确定显著水平α=0.05（两尾概率）。

（3）检验计算

均数标准误

统计量t值

自由度

df=n-1=16-1=15

（4）统计推断

由自由度df=15和显著水平α=0.01查附录3得临界t值t_0.01（15）=2.947。由于实得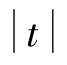=6.667＞t_0.01（15）=2.947，故p＜0.01，应否定H₀，接受H_A，推断新、旧工艺的每100g山楂出果冻量差异极显著（用**表示），亦即采用新工艺可提高每100g山楂出果冻量。

二、两个样本平均数的假设检验

两个样本平均数的假设检验，就是由两个样本平均数之差去推断两个样本所在总体平均数μ₁和μ₂是否有差异，即检验无效假设H₀：μ₁=μ₂（或μ₁≤μ₂，或μ₁≥μ₂）和备择假设H₀：μ₁≠μ₂（或μ₁＞μ₂，或μ₁＜μ₂）这类问题。实际上这是检验两个处理的效应是否一样。

1.成组资料平均数的假设检验

成组资料是指在试验调查时分别从两个处理中各随机抽取一个样本而构成的资料。其特点是两组数据相互独立，各组数据的个数不一定相等。在各种试验资料中，两个处理的完全随机试验资料属于成组资料。成组资料平均数的假设检验也有u检验和t检验之分。

（1）u检验 如果两个样本资料都服从正态分布，且总体方差和已知；或者总体方差未知，但两个样本都是大样本时，平均数差数的分布呈正态分布，因而可采用u检验法来检验两个样本平均数的差异显著性。由两均数差数抽样分布理论可知，两个样本平均数和的差数标准误，如式5-3、式5-4所示。

并有

在H₀：μ₁=μ₂下，正态离差u值为

根据以上公式即可对两个样本平均数的差异进行假设检验。如果总体方差未知，但n₁≥30，n₂≥30时，可由样本方差、估计总体方差、。

【例5-5】某食品厂在甲、乙两条生产线上各测了30个日产量如表5-3和表5-4所示，试检验两条生产线的平均日产量有无显著差异。

表5-3 甲生产线日产量记录 单位：kg

表5-4 乙生产线日产量记录 单位：kg(www.xing528.com)

本例两个样本均为大样本，符合μ检验条件。

①建立假设：

H₀：μ₁=μ₂，即两条生产线的平均日产量无差异。

H_A：μ₁≠μ₂，即两条生产线的平均日产量有差异。

②确定显著水平：α=0.01。

③检验计算：

④统计推断：由α=0.01查附表2得μ_0.01=2.58。由于实际=3.281＞μ_0.01=2.58，故p＜0.01，应否定H₀，接受H_A。这说明两条生产线的日平均产量有极显著差异，甲生产线日均产量高于乙生产线日均产量。

（2）t检验 当两个样本资料服从正态分布，且σ²₁=σ²₂=σ²时，不论是大样本还是小样本，都有下式服从具有自由度df=n₁+n₂-2的t分布（n₁、n₂为两个样本含量）：

在H₀：μ₁=μ₂下，上式为

当两样本含量相等（n₁=n₂=n）时，则

此时自由度为df=2（n-1）。

【例5-6】海关检查某罐头厂生产的出口红烧花蛤罐头时发现，虽然罐头外观无胖听现象，但产品存在质量问题。于是从该厂随机抽取6个样品，同时随机抽取6个正常罐头测定其SO₂含量，测定结果如表5-5所示。试检验两种罐头的SO₂含量是否有差异。

表5-5 正常罐头与异常罐头SO₂含量 单位：μg/mL

①建立假设

H₀：μ₁=μ₂，即两种罐头的SO₂含量无差异。

H_A：μ₁≠μ₂，即两种罐头的SO₂含量有差异。

②确定显著水平：α=0.01（两尾概率）。

③检验计算

本例的两个样本容量相等（n₁=n₂=6），所以

④统计推断：由df=10和α=0.01查附表3得t_0.01（10）=3.169。由于实际=22.743＞t_0.01（10）=3.169，故p＜0.01，应否定H₀，接受H_A。即两种罐头54的SO₂含量差异极显著，异常的罐头SO₂含量高于正常的，该批罐头已被硫化腐败菌感染变质了。

（3）近似t检验-t′检验 在两个样本所属总体的方差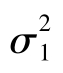和未知，但根据专业知识或统计方法能确知时，作t检验的均数差数标准误就不能再用由两个样本方差的加权平均数作总体方差σ²的估计值，而应分别由和去估计和，于是均数差数标准误变为

此时的就不再准确地服从自由度为df=n₁+n₂-2的t分布，而只是近似地服从t分布，因而不能直接作t检验。针对这一问题，Cochran和Con提出了一个近似t检验法。该法在作统计推断时，所用临界t值不是直接由t值表（附表3）查得，而须作一定矫正。矫正临界t值公式为

式中：；；df₁=n₁-1；df₂=n₂-1。

如果n₁=n₂=n，因，由上式容易导出t′_α=t_α（df）（df=n-1）。此时可直接由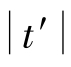与由α和df=n-1查附表3得到的临界t值与t_α（df）比较后作出推断。

【例5-7】在作各种大米的营养价值的研究中，测定了籼稻米的粗蛋白含量5次，得平均数=7.32mg/100g，方差=1.06（mg/100g）²；另测定了糯稻米的粗蛋白含量5次，得平均数=7.62mg/100g，方差=0.11（mg/100g）²。试检验两种大米的粗蛋白含量有无显著差异。

经方差同质性检验，可知本例的两个样本方差存在显著差异，因此只能做近似t检验。

①建立假设：

H₀：μ₁=μ₂，即两种大米的粗蛋白含量无差异。

H_A：μ₁≠μ₂，即两种大米的粗蛋白含量有差异。

②确定显著水平：α=0.05。

③检验计算：

④统计推断：由df₁=9和df₂=4及显著水平α=0.05查附表3得t值t_0.05（9）=2.262，t_0.05（4）=2.776。因此

由于实得=0.838＜t′_0.05=2.350，故p＞0.05，应接受H₀：μ₁=μ₂，故推断两种大米的粗蛋白含量无显著差异。

2.成对资料平均数的假设检验

若试验设计是将条件、性质相同或相近的两个供试单元配成一对，并设有多个配对，然后对每一配对的两个供试单元分别随机地给予不同处理，这样的试验叫做配对试验。它的特点是配成对子的两个试验单元的非处理条件尽量一致，不同对子的试验单元之间的非处理条件允许有差异。配对试验的配对方式有自身配对和同源配对两种。所谓自身配对是指在同一试验单元上进行处理前与处理后的对比，如同一食品在储藏前后的变化等。同源配对是指将非处理条件相近的两试验单元组成对子，然后分别对配对的两个试验单元施以不同的处理。如按产品批次划分对子，在每一批产品内分别安排一对处理的试验，或同一食品平分成两部分来安排一对处理的试验等。配对试验因加强了配对处理间的试验控制（非处理条件高度一致），使处理间可比性增强，试验误差降低，因而试验精度较高。

从配对试验中获得的观测值因是成对出现的，故叫做成对资料。与成组资料相比，成对资料中两个处理的数据不是相互独立的，而是存在着某种联系。因而对其作样本平均数的差异显著性检验时，应从成对数据的角度切入。

可以将两个处理设想为两个总体。第一个总体观测值为x₁₁，x₁₂，…，x_1∞，第二个总体观测值为x₂₁，x₂₂，…，x_2∞。两个总体观测值间由于存在着一定联系而一一配对，即（x₁₁，x₂₁），（x₁₂，x₂₂），…，（x_1i，x_2i），…，（x_1∞，x_2∞）。每对观测值之间的差数为：d_i=x_1i-x_2i（i=1，2，…，∞）。差数d₁，d₂，…，d_∞组成差数总体，总体平均数用μ_d表示。实际上，μ_d=μ₁-μ₂。所以，在μ₁=μ₂时，μ_d=0；反之μ_d≠0。

在上述两总体中抽出n对数据组成样本，每对数据的差数组成差数样本，即d₁，d₂，…，d_n。

差数样本的平均数

差数标准差

差数均数标准误

故服从自由度为df=n-1的t分布。在无效假设H₀：μ₁=μ₂，即μ_d=0时，t值为

于是便可对成对资料平均数进行假设检验。