汽车电工电子技术：电感元件在交流电路中的功耗为零！

1.电感元件上电流与电压关系

假设线圈只有电感L，电阻R 可以忽略不计，则称之为纯电感，今后所说的电感如无特殊说明就是指纯电感，当电感线圈中通过交流电流i 时，其中产生自感电动势 eL，设电流i电动势 eL和电压u 的参考方向如图2-8（a）所示。

设有电流i=Imsin ωt流过电感L，则代入式（2-14）得电感上的电压u 为

即u 和i 也是一个同频率的正弦量。表示电压u 和电流i 的正弦波形，如图2-8（b）所示。

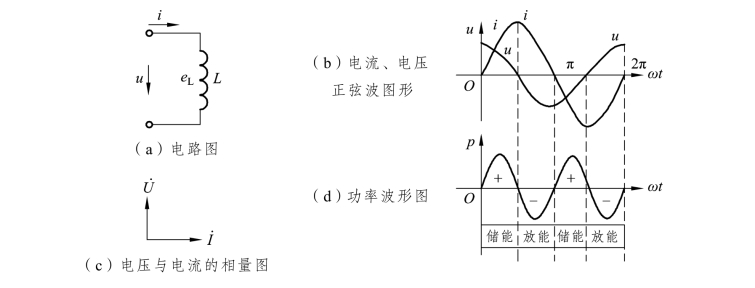
图2-8　电感元件交流电路

比较以上u、i 表达式可知，在电感元件电路中，电流在相位上比电压滞后90°，且电压与电流的最大值及有效值符合

即在电感元件电路中，电压的幅值（或有效值）与电流的幅值（或有效值）之比为 ω L，显然它的单位也为欧姆。电压U 一定时，ω L越大则电流I 越小。可见它具有对电流起阻碍作用的物理性质，所以称为感抗。用XL表示，表达式为

(www.xing528.com)

感抗与电感L 频率f 成正比，因此电感线圈对于高频电流的阻碍作用很大，而对直流则可视作短路。还应该注意，感抗只是电压与电流的幅值或有效值之比，而不是它们的瞬时值之比。

如用相量表示电压与电流的关系，则

式（2-17）也表示了电压与电流的有效值关系及相位关系，即：电压与电流的有效值符合欧姆定律（U=IXL），相位上的电压超前电流90°，因电流相量I˙乘上j 后向前旋转90°，所以称jXL为复感抗。电压和电流的相量图如图2-8（c）所示。

2.电感元件的功率与储能

知道了电压u 和电流i 的变化规律和相互关系后，便可找出瞬时功率的变化规律，即

可见，p 是一个幅值为UI，以2ω 角频率随时间变化的交变量，如图2-8（d）所示。当u 和i 正负相同时，p 为正值，电感处于受电状态，它从电源取用电能；当u 和i 正负相反时，p 为负值，电感处于供电状态，它把电能归还电源。电感元件电路的平均功率为零，即电感元件的交流电路中没有能量消耗，只有电源与电感元件间的能量互换。这种能量互换的规模用无功功率Q 来衡量，规定无功功率等于瞬时功率 pL的幅值，即

无功功率的单位是乏（var）或千乏（kvar）。