正弦量交流电路的基本概念|汽车电工电子技术

电流和电压的大小和方向均随时间按正弦规律变化，叫作正弦交流电。正弦交流电是日常生活和科技领域中最常见、应用最广泛的一种电的形式。汽车发电机产生的就是交流电。下面我们就来了解一下正弦交流电的基本概念。

1.正弦交流电的周期、频率和角频率

汽车发电机产生的交流电，其大小和方向均随时间按正弦规律变化。交流电随时间变化的快慢程度可以由周期、频率和角频率从不同的角度来反映。

1）频 率

单位时间内，正弦交流电重复变化的循环次数称为频率。频率用f 表示，单位是赫兹（Hz）。例如，我国电力工业的交流电频率规定为 50 Hz，简称工频；少数发达国家采用的工频为60 Hz。显然，频率越高，交流电随时间变化得越快。

2）周 期

交流电每重复变化一个循环所需要的时间称为周期，如图2-1 所示。周期用T 表示，单位是秒（s）。

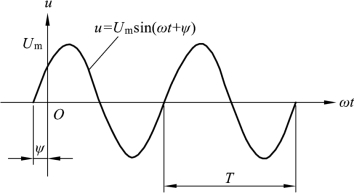
图2-1　正弦交流电示意图

显然，周期和频率互为倒数关系，即

由上式可知，周期越短频率越高。周期的大小同样可以反映正弦量随时间变化的快慢程度。

3）角频率

正弦函数总是与一定的电角度相对应，所以正弦交流电变化的快慢除了用周期和频率描述外，还可以用角频率ω 表示。角频率ω 表示正弦量每秒经历的弧度数，其单位为弧度/秒（rad/s）。由于正弦量每变化一周所经历的电角弧度是2 π，因此角频率为

周期、频率和角频率从不同的角度反映了同一个问题：正弦量随时间变化快慢程度。式（2-1）反映三者之间的数量关系。在实际应用中，频率的概念用得最多。

2.正弦交流电的瞬时值、最大值和有效值

1）瞬时值

交流电每时每刻均随时间变化，它对应任一时刻的数值称为瞬时值。瞬时值是随时间变化的量，因此要用英文小写斜体字母表示为u、i。图2-1 所示为正弦交流电压的瞬时值，可用正弦函数式来表示

2）最大值

交流电随时间按正弦规律变化振荡的过程中，出现的正、负两个振荡最高点称为正弦量的振幅，其中的正向振幅称为正弦量的最大值，一般用大写斜体字母加下标m 表示为Um、Im。注意：式（2-2）所示的正弦交流电的一般表达式中，其最大值恒为正值。

正弦量是一个等幅振荡的、正负交替变化的周期函数。对正弦量的数学描述可以用sin函数，也可以用cos 函数，式（2-2）采用的是sin 函数，本书中均采用sin 函数。

对于大小和方向都随时间变动的电流来说，更有必要选定参考方向了。因为电流的实际方向随时在变动，如不规定电流的参考方向，就很难用一个表达式来准确表达任何时刻电流的大小及其实际方向。参考方向的规定与前面一样，一般用箭头来表示。当电流的实际方向与所选定的参考方向一致时，电流值为正，反之就为负。因此，电流的参考方向只是用来确定某一时刻电流的正负号。

3）有效值

正弦交流电的瞬时值是变量，无法确切地反映正弦量的做功能力。用最大值表示正弦量的做功能力，显然夸大了作用，因为正弦交流电在一个周期内只有两个时刻的瞬时值等于最大值的数值，其余时间的数值都比最大值小。为了确切地表示正弦量的做功能力，以及方便地计算和测量正弦量的大小，实用中人们引入了有效值的概念。

有效值是根据电流的热效应定义的。如图2-2 所示，让两个相同的电阻R 分别通过正弦交流电流i 和直流电流I。如果在相同时间t 内，两种电流在两个相同的电阻上产生的热量相等（即做功能力相同），就把图2-2（b）中的直流电流I 定义为图2-2（a）中交流电流i 的有效值。显然，与正弦量热效应相等的直流电的数值称为正弦量的有效值。

图2-2　电流的有效值

正弦交流电的有效值是用热效应相同的直流电的数值来定义的，因此，正弦交流电的有效值通常用与直流电相同的大写斜体字母U、I 来表示。值得注意的是：正弦量的有效值和直流电虽然表示符号相同，但它们所表达的概念是不同的。

实验结果和数学分析都可以证明，正弦交流电的最大值和有效值之间存在如下数量关系：

在电路理论中，通常所说的交流电数值如不做特殊说明，均指交流电的有效值。在测量交流电路的电压、电流时，仪表指示的数值通常也都是交流电的有效值。各种交流电器设备铭牌上的额定电压和额定电流一般均指其有效值。(www.xing528.com)

正弦交流电的瞬时值表达式可以精确地描述正弦量随时间变化的情况。正弦交流电最大值表征了其振荡的正向最高点，其有效值则确切地反映出正弦交流电的做功能力。显然，最大值和有效值可从不同的角度说明正弦交流电的“大小”情况。

3.正弦交流电的相位、初相

1）相 位

正弦量随时间变化的核心部分是解析式中的（ω t+ψ ），它反映了正弦量随时间变化的进程，是一个随时间变化的电角度，称为正弦量的相位角，简称相位。当相位随时间连续变化时，正弦量的瞬时值随之做连续变化。

2）初 相

对应t=0 时的相位ψ 称为初相角，简称初相。初相确定了正弦量计时初始正弦量的状态。为保证正弦量解析式表示上的统一性，通常规定初相不得超过 ±180°。

在上述规定下，初相为正角时，正弦量对应的初始值一定是正值；初相为负角时，正弦量对应的初始值则为负值。在波形图上，正值初相角位于坐标原点左边零点（指波形由负值变为正值所经历的0 点）与原点之间（如图2-3 所示 i1的初相）；负值初相位于坐标原点右边零点与原点之间（如图2-3 所示 i2的初相）。

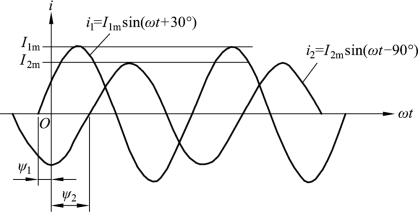
图2-3　正弦交流电的相位差

3）相位差

为了比较两个同频率的正弦量在变化过程中的相位关系和先后顺序，我们引入相位差的概念，相位差用φ 表示。如图2-3 所示的两个正弦交流电流的解析式分别为

则两电流的相位差为

可见，两个同频率正弦量的相位差等于它们的初相之差，与时间t 无关。相位差是比较两个同频率正弦量之间关系的重要参数之一。

若已知ψ1=30°，ψ2=90°，则电流 i1与 i2在任意瞬时的相位之差为

相位差角φ 和初相的规定相同，均不得超过 ±1 80°。

当两个同频率正弦量之间的相位差为零时，其相位上具有同相关系，只有电阻元件上的电压、电流关系为同相关系，因此同相的电压、电流只构成有功功率；当两个同频率正弦量之间的相位差为90°时，它们在相位上具有正交关系。动态元件L 和C 上的电压、电流关系正是这种正交关系。若两个同频率正弦量之间的相位差是180°，称它们之间的相位关系为反相关系。除此之外，两个同频率正弦量之间还具有超前、滞后的相位关系。

【例1】 已知工频电压有效值U=220 V，初相ψu=60°。工频电流有效值I=22 A，初相ψi=-3 0°。求其瞬时值表达式、波形图及它们的相位差。

解：工频电角频率ω=314 rad/s

电压的解析式为

电流的解析式为

电压与电流的波形图如图2-4 所示。

电压与电流的相位差为

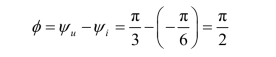
显然，一个正弦量的最大值（或有效值）、角频率（或频率、周期）及初相一旦确定后，它的解析式和波形图的表示就是唯一、确定的。我们把最大值（或有效值）、角频率（或频率、周期）初相称为正弦量的三要素。

图2-4　例1 中u、i 波形图