贝叶斯网络(Bayesian Networks,BN)也被称为因果概率网络(Causal Probability Networks)、概率网络(Probability Networks)、置信网络(Belief Networks),它是一个涉及统计学、图论等多个学科的交叉研究问题,本质上是一个表示变量间概率依赖关系的有向无环图。
贝叶斯网络理论的数学思想源自于18世纪数学家和神学家Thomas Bayes提出的贝叶斯公式:
设A1,A2,…,An为样本空间Ω的一个划分,且P(Ai)>0(i=1,2,…,n),则对于任何一事件B(P(B)>0),有以下关系:
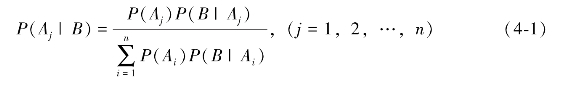
在贝叶斯公式中,可以把Aj看做是某个假设,而B表示某一个影响假设成立概率的证据,那么由此公式可以计算出当加入新证据B的情况下,假设Aj成立的概率。而这一数学逻辑也正是推理所需要的思路。
在贝叶斯公式的基础上,后来的学者们把图论引入到概率理论中来,创建了用来表示变量间连接概率的图形模式——贝叶斯网络,提供了一种自然的信息表示方法,用来表达变量之间的因果关系。作为一种有向无环图,贝叶斯网络中的节点表示领域内的变量,而节点之间的边表示变量之间的条件依赖关系。因此,贝叶斯网络的定义也由网络结构和条件概率分布公式两部分组成。
定义4.1 贝叶斯网络它是一个二元组B=(Bs,Bp),其中Bs=(X,E)为贝叶斯网的结构,是一个有向无环图;X={X1,X2,…,Xn},表示图中的每一个节点对应的随机变量集,节点的状态对应随机变量的值,E为有向边集,表示节点(变量)之间的条件(因果)依赖关系;Bp={P(Xi|Pa(Xi))}表示贝叶斯网络的条件概率分布集合,每个节点都有一个条件概率表,用来表示对于其父节点集的条件概率。(https://www.xing528.com)
对于一个有n个节点的贝叶斯网络,它的联合概率函数定义如下式:
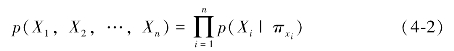
如图4-1所示,节点C、S、V构建了一个简单的贝叶斯网络结构,条件概率参数如图所示,则它们的联合概率分布计算如下:
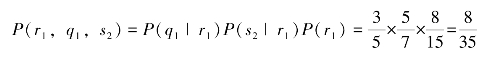
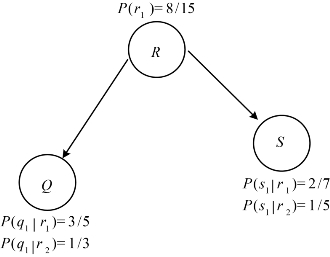
图4-1 简单的贝叶斯网络联合概率分布计算实例
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




