事故概述 某高速公路路段，为东西走向。午夜3时许，一辆在主车道行驶的重型厢式货车（甲车）沿公路自西向东行驶至事故路段时，驾驶员忽然发现有一辆重型半挂货车（乙车）在前方同车道不远处同向行驶，他立即向左打方向盘回避并实施了紧急制动，但由于两车相距太近，甲、乙两车还是发生了追尾碰撞，甲车车头右侧碰撞乙车左侧车尾，碰撞后两车均向前滑行一段距离后停止。碰撞造成甲车车头右侧严重损伤，前排右侧座位乘客当场死亡。事故路段为干燥混凝土路面。现场图和现场照片参看图9-8和图9-9。
事故分析 与前面高速公路的追尾碰撞案例相比，本案有两个新的特点：首先，在前面的案例中，追尾车都是在没有实施制动的情况下与前车相撞，碰撞后也没有实施制动，因为追尾碰撞属于完全非弹性碰撞，所以碰撞后两车连在一起以同一速度运动。然而本案中，甲车驾驶员在碰撞前就实施了紧急制动，直至接近停止。由于甲车紧急制动轮胎与路面的摩擦系数大于乙车缓慢制动的摩擦系数，虽然两车碰撞后的速度相同，但摩擦力的差别使两车逐渐分离。本案的第二个特点是被追尾的乙车滑行距离很短。按现场图的数据以及下面我们推算出的两车碰撞点的位置估算，乙车碰撞后仅滑行不到20m就停下，若把乙车实施制动的反应时间考虑在内，运用式（2-31）计算两车碰撞后的共同速度，只有约20km/h，乙车碰撞前的行驶车速将更低，这与现场照片显示的甲车车头损伤并不算严重的情况不符。如图9-9c所示，甲车仅驾驶楼右侧凹陷，但底盘和驾驶楼左侧损伤不大，驾驶员也只受轻微皮外伤。甲车仅载10t货物，在高速公路上正常行驶，若与缓慢的低于20km/h车速的乙车相撞，后果将极其惨重。为了解释这个不正常的现象，我们调查了事故的发生过程。乙车驾驶员陈述：事故发生前他发现前方的大货车变道，他踩制动踏板减速，随后就发生了被甲车追尾，由于当时他的脚踩在制动踏板上，于是继续踩制动踏板把车停下。这样，乙车的制动不存在反应时间，碰撞后乙车全程处于缓慢制动状态，所以其滑行距离比一般案例中被追尾车滑行距离要短得多。
图9-8 重型厢式货车追尾碰撞重型半挂货车事故现场图
图9-9 事故现场照片图（案例9-4）
由于甲车在路面上留下了制动的轮胎印迹，本案我们优先利用甲车的制动印迹计算两车碰撞后的共同速度。
车速计算 甲、乙两车的碰撞属于完全非弹性碰撞，动量守恒定律表达式为
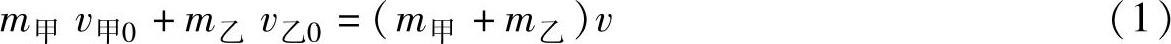
式中，m甲、m乙分别为甲、乙两车的质量，根据行驶证、过磅单和办案方提供的数据，m甲=20590kg，m乙=112000kg；v甲0和v乙0分别为甲、乙两车碰撞前的车速；v为两车碰撞后的共同速度。
甲车碰撞前已实施紧急制动直至停止，可依据甲车碰撞后的制动距离运用制动印公式计算碰撞后两车的共同速度v为
式中，μ甲为甲车轮胎与路面的摩擦系数，根据表2-2，对于干燥混凝土路面，车速超过48km/h时取值为0.60～0.75。大货车制动性能偏低，取μ甲=0.60。S甲为甲车碰撞后的滑行距离，它等于从碰撞点到甲车停止位置车头前缘的距离。从现场图上看不出具体的碰撞点。为此，类似案例9-3，我们利用甲车驾驶楼碰撞碎片的分布起点处为一些细小的白色漆片，可近似认为它们落地后不再往前滑动，根据办案方提供的数据，散落物起点至甲车车头前缘的距离为4.00m。则
S甲=L+4.00（3）
式中，L为漆片平抛的距离，可用式（2-6）计算：
变换得
式中，h为漆片抛出的高度，近似取甲车高度的一半，根据车辆信息，甲车高2.495m，则
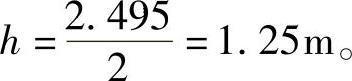
代入式（4）得
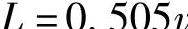(www.xing528.com)
代入式（3），得
将相关数据代入式（2），可得出一个二次代数方程为
解出
为求解v甲0和v乙0，还需引入甲车的有效碰撞速度定义式：
式中，v甲e为甲车的有效碰撞速度，可依据甲车乘员受伤程度计算。甲车前排乘员死亡为形变驾驶楼挤压所致，不属于此范围，而驾驶员仅受轻微皮外伤，类似前面案例，取au=30g，则
代入式（6），得
联立式（1）和式（7），可解得
v甲0还不是甲车事故发生时的行驶车速，因为碰撞前甲车已实施了一段距离的制动。将v值代入式（5），得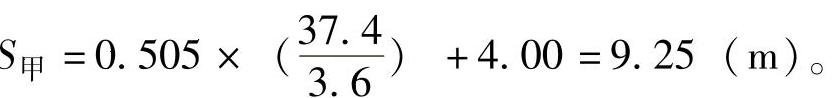
根据现场图，甲车轮胎印迹总长为14.10m，则甲车碰撞前的制动印迹长为S′甲=14.10m-9.25m=4.85m。可运用末速不为零的制动印公式（2-23）计算甲车在事故发生时的行驶车速：
根据表2-3，取t=0.50s，则
乙车碰撞前的行驶车速仅为30.9km/h，可以判断其实施制动前的车速也低于60km/h的最低限速。造成乙车车速偏低的原因也是因为超载。乙车牵引车的准牵引质量为41.47t，实际牵引103t。
结论 肇事重型厢式货车事故发生时的行驶车速约为83km/h。
肇事重型半挂货车事故发生时的行驶车速约为31km/h。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
