道路交通事故车速鉴定的方法和案例分析

1.功

在力学中，对于恒力，功定义为力与力的作用点在力的方向的位移的乘积，即W=Fx（3-26）式中，W代表功；F为作用于x方向的恒力；x为F的作用点沿x方向的位移。图3-14所示为光滑水平面上，一个物体在水平恒力F作用下的运动。作用在物体上还有竖直方向的重力和支持力N，但它们的作用点在竖直方向没有位移，所以只有水平力F做功。

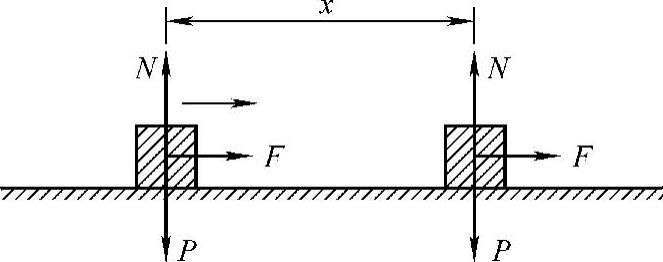
图3-14　恒力做功

在一般情况下，力与物体位移的方向不一定相同，如图3-15所示。设力与位移方向夹一个角θ，把力F分解为沿水平和竖直方向的两个分力F₁和F₂。F₂与位移方向垂直不做功，只有F₁做功，而F₁=Fcosθ。故此时功定义为

从式（3-27）可看出：

（1）θ=0°，即力与位移x的方向一致时，cosθ=1，W=Fx，F对物体做正功。例如牵引车牵拉事故车辆时，牵引力做的就是正功。

（2）θ=180°，即力与位移x的方向相反时，cosθ=-1，W=-Fx，W为负值，F对物体做负功。例如在汽车制动过程中，轮胎与路面的摩擦力与汽车位移的方向相反，摩擦力对汽车做负功。

（3）当θ=90°，即力与物体位移的方向垂直时，cosθ=0，W=0，即该力不做功。例如在水平路面上，作用于汽车的重力和地面对汽车的支持力都不做功。

若同时有数个力作用于物体，则总功等于各力所做的功的代数和。例如汽车在水平路面上加速行驶，牵引力F做正功，滚动摩擦阻力f_r和空气阻力F_w做负功

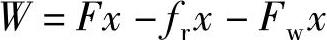
以上讨论的是恒力做功。可以证明，对于变力，例如汽车受到的撞击力，空气阻力等就属于变力，此时功的定义式（3-27）改变为一个定积分：

其中，F可表示为x的函数。

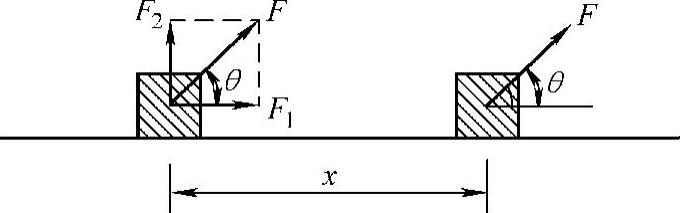
图3-15 外力与位移夹θ角做功的计算

功的单位为焦耳，简写为J，1J=1N·m。

作为计算变力做功的例子，我们以汽车碰撞中撞击力做功为例。前面讨论中指出，在高速汽车的碰撞中，撞击力是一种“塑性力”，即碰撞造成的变形基本不能恢复。国外用小轿车进行撞墙试验，图3-16所示为典型的汽车撞击力与汽车塑性形变量的试验关系^[3]。由图可见，在一定范围内，撞击力与形变量的大小成正比，所以汽车受到撞击力作用时，类似一个“塑性弹簧”（弹簧具有作用力与形变量成正比的特性，在这方面，撞击力相似，只是前者能够恢复形变，后者不能，故称为“塑性弹簧”）。于是撞击力可以表示为

F=Kx(www.xing528.com)

图3-16 某一型号小轿车与墙壁碰撞形 变量与撞击力的关系

式中，K为塑性系数。当形变量由0→x时，撞击力做功为

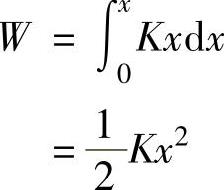
国外试验者还发现一个特点，不同牌号的小轿车因刚性不同，塑性系数K并不相同，但单位质量的塑性系数，即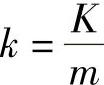

却近似相同。于是可以把汽车碰撞中撞击力做功表示为

式（3-29）在车速鉴定中没有直接的应用。但结合下面将要讨论的动能定理，我们将证明，前面关于小轿车的有效碰撞速度与碰撞塑性形变量成正比的试验公式（3-13）其理论依据就是式（3-29）表示的撞击力做功与塑性形变量平方成正比这一特性。

2.功率

功率表示单位时间内所完成的功

式中，P代表功率，单位为瓦（W），1W=1J/s。在汽车理论中，用的是“千瓦”，简写为kW，1kW=1000W。

在道路交通事故的车速鉴定中，计算车速涉及的是“汽车的额定功率”，它代表汽车发动机在单位时间内最多能做多少功。汽车的额定功率是一个恒定值，它标示在汽车的技术参数中。

汽车的额定功率是恒定的，但汽车在行驶中所需要的牵引力却是变化的。汽车驾驶员都了解，汽车在起动时，为了获得尽可能大的牵引力，需要挂低速档，以增大变速器的传动比，降低车速；而在高速平稳行驶中则要减小牵引力，需要挂高速档，以降低变速器的传动比。设汽车在牵引力F的作用下，在一段很小的时间间隔Δt内位移为Δx，由于Δx很小，F可认为是不变的，则牵引力做功可表示为FΔx，于是Δt时间内的功率为

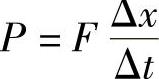
当Δt取得很小时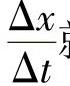，就代表汽车的瞬时速度，由此得

式（3-31）反映了前述驾驶员的经验：在额定功率不变的情况下，在汽车起步阶段，为了获得最大的牵引力就需要低速起动，而在高速行驶时则需要减小牵引力。