机动车碰撞的特点及车速鉴定方法

前面提到了动量守恒公式在实际应用中的局限性，即对于大多数碰撞事故，我们一般只能列出一个方向的动量守恒公式，于是便出现一个方程不能求解两个未知数的难题。解决的办法，是设法找到第二个包含v₁₀和v₂₀的方程。为此，首先需要研究机动车碰撞的性质。

我们在交通事故现场常常会看到这样的景象：有的时候机动车碰撞后互相弹开分离，有的时候又紧紧连在一起。这是什么缘故呢？力学碰撞理论指出，这是由于碰撞性质不同所致。能够互相弹开的碰撞称为“弹性碰撞”，不能弹开、碰撞后连在一起的碰撞称为“非弹性碰撞”，仔细区分可划分为如下三类。

（1）完全弹性碰撞。所谓完全弹性碰撞是指两个弹性的物体间的碰撞，弹性物体碰撞后能够完∙全∙恢∙复∙自∙身∙的∙形∙变∙。日常生活中两个橡皮球的碰撞便是典型的例子。其实我们熟悉的桌球间的碰撞也属于完全弹性碰撞，它们在击打后没有在球上留下形变的痕迹，只是因为它们在碰撞中的形变很小，不像橡皮球的形变能用肉眼观察得到。图3-5所示为两个弹性物体碰撞的过程。

图3-5a所示为碰撞前质量为m₁和m₂的两球分别以v₁₀、v₂₀的速度互相接近；图3-5b所示为两球开始互相接触；图3-5c所示为两球互相挤压达到最大形变，为恢复自身形变产生了作用于对方的弹性力f₂和f₁，在此二力作用下两球重新分离；图3-5d所示为两球完全恢复自身的形变，并以v₂-v₁的分离速度互相分离。

（2）完全非弹性碰撞。所谓完全非弹性碰撞是指两个（也可以是其中一个）碰撞后完全不能恢复自身形变的塑性物体之间的碰撞。日常生活中两个橡皮泥做成的小球的碰撞就是典型的完全非弹性碰撞。图3-6所示为完全非弹性碰撞的过程。

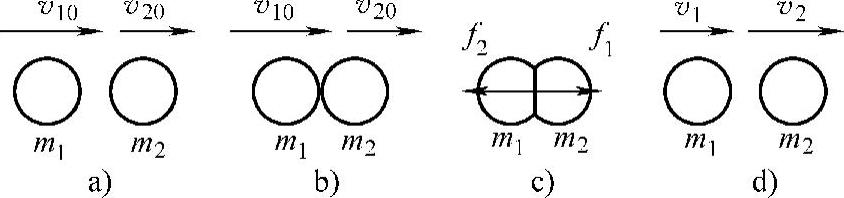
图3-5 完全弹性碰撞

图3-6a所示为质量为m，和m。的两球碰撞前分别以v_l0、v₂₀的速度互相接近；图3-6b所示为两球开始互相接触；图3-6c所示为两球互相挤压达到最大形变，但因为两球为塑性物体．完全没有为恢复自身形变而作用于对方的弹性力．所以两球碰撞后连在一起不分离；图3-6d所示为两球连成一体以共同速度v运动。

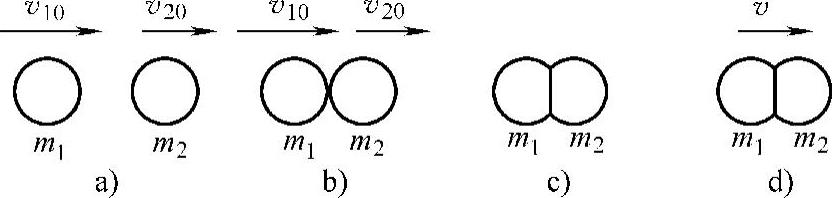
图3-6 完全非弹性碰撞

(3)非完全弹性碰撞。其实在日常生活中，一般物体既非橡皮球那样的弹性物体，也非橡皮泥那样的塑性物体，而是介于二者之间，即在碰撞中会产生部分永久性的形变．但也具有部分为恢复自身形变而作用于对方的弹性力，使碰撞后互相分离。汽车在速度不高的情况下的碰撞就属于这种情形。我们从经验中观察到，两辆以较低速行驶的汽车的对撞，会使两车都留下一些永久性形变，但两车在碰撞中也具有部分为恢复自身形变而作用于对方的弹性力，结果使碰撞后两车互相弹开。图3-7所示为非完全弹性碰撞的过程。

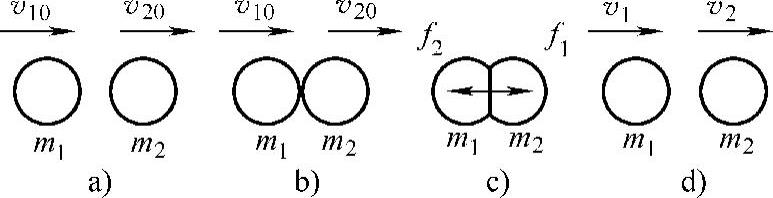
图3-7a所示为质量为m₁和m₂的两球分别以速度v₁₀、v₂₀互相接近；图3-7b所示为两球开始互相接触；图3-7c所示为两球互相挤压达到最大形变，由于两球为部分弹性物体，仍然具有部分为恢复自身形变而作用于对方的较小的作用力f₂和f₁；图3-7d所示为两个小球带着部分永久性的形变以分离速度v₂-v₁互相分离。

机动车之间的碰撞属于哪类碰撞呢？有人说，机动车都是钢铁制成的，所以它们的碰撞属于完全弹性碰撞。这种看法是错误的。事实上，两辆汽车即使在较低速情况下相撞，例如小轿车以30km/h的速度互相对撞，从经验中我们知道，两车车头都会产生相当严重的不能恢复的永久性形变（又称为塑性形变），但碰撞后两车仍然会分离，说明碰撞属于非完全弹性碰撞。然而对于小轿车的追尾碰撞或高速情况下的对撞，我们观察到两车碰撞后会连在一起或以大致相同的速度朝一个方向运动，这说明碰撞的性质属于或接近完全非弹性碰撞。所以，机动车碰撞的性质介于完全非弹性碰撞与非完全弹性碰撞之间。

为了定量地描述碰撞的性质，力学中引入了一个“恢复系数”，它代表物体的弹性程度，即物体恢复自身形变的能力。恢复系数e定义为

式（3-8）表示，恢复系数e等于分离速度v₂-v₁与接近速度v₁₀-v₂₀之比。对于完全弹性碰撞，可以证明v₂-v₁=v₁₀-v₂₀，故e=1^[1]；对于完全非弹性碰撞，因为碰撞后两个物体连在一起以同一速度运动，即v₂=v₁=v，v₂-v₁=0，故e=0。一般机动车的碰撞恢复系数为0～1或趋于零。恢复系数越趋近零，说明碰撞越接近完全非弹性碰撞。

(www.xing528.com)

图3-7 非完全弹性碰撞

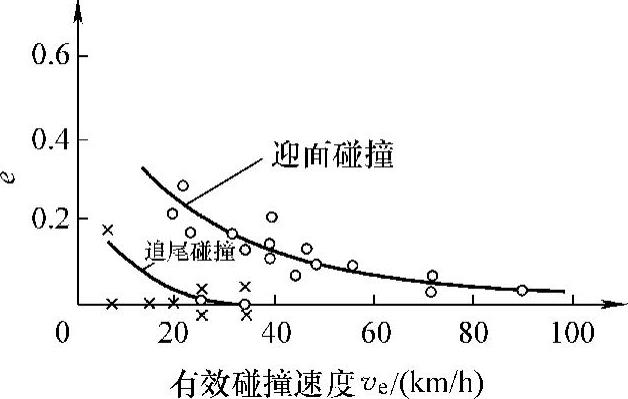
图3-8 有效碰撞速度与恢复系数的关系

图3-8所示为国外研究者对小轿车的迎面碰撞和追尾碰撞的恢复系数随“有效碰撞速度”v_e（这个概念在下一节进行定义）增加而改变的试验结果。由图中可以看出，对于追尾碰撞，只要有效碰撞速度v_e超过20km/h，恢复系数e就等于零，即小轿车的追尾碰撞实际上都属于完全非弹性碰撞。这是因为小轿车的行李箱是空的，刚性很弱，从经验中我们知道，轻微的追尾碰撞就会给小轿车行李箱造成凹陷，碰撞后两车大都连在一起，这符合完全非弹性碰撞的特征。对于小轿车的迎面碰撞，由于小轿车发动机前置，车头刚性较强，从图上看，当v_e=20km/h，即两车在低速行驶情况下相撞，恢复系数约为0.4。但当v_e=60km/h，即两车在中速情况下对撞，e即降低到约0.1，即接近完全非弹性碰撞。在v_e达到80km/h以上时，e已接近零，完全可以视为完全非弹性碰撞。

掌握了汽车在中速以上碰撞接近完全非弹性碰撞的特点，对于一些疑难碰撞事故的车速鉴定是很有帮助的。特别是现在小轿车普遍在制动系统中配备了ABS，实施紧急制动一般在路面上没有留下明显的轮胎印迹，这给车速鉴定带来很大的困难。但若碰撞事故的另一辆车在路面上留有轮胎或车身刮地的痕迹，则我们可以利用完全非弹性碰撞后两车以同一速度运动的特点，以有痕迹的那辆车来计算两车的共同速度。最常见的是小轿车与二轮摩托车或自行车的碰撞，现场只有二轮摩托车或自行车的刮地痕迹而没有小轿车的轮胎制动印迹。考虑到二轮摩托车的刚性不会比小轿车尾部更强，自行车刚性就更低，所以，小轿车或一般汽车与二轮摩托车、自行车的碰撞均属完全非弹性碰撞。这样，在小轿车与二轮摩托车的碰撞事故中，只需要利用二轮摩托车车身刮地痕迹计算出二轮摩托车刮地滑行的初速度即可，它就等于小轿车碰撞后的速度。

【例3-4】　一辆质量为1420kg的小轿车（甲车）在交叉路口处与一辆质量为m₂=240kg（连乘员）的二轮摩托车（乙车）发生横向碰撞，甲车的车头碰撞乙车的左侧车身。碰撞后乙车沿甲车行驶方向刮地滑行28.50m停下；小轿车从碰撞点滑行18.20m停下，由于甲车配备有ABS，路面上没有留下甲车轮胎的制动印迹。求小轿车在事故发生时的行驶车速。

解：这个案例中由于甲车配备有ABS，在路面上没有留下轮胎的制动印迹，制动距离不明．故不能运用制动印公式计算甲车碰撞后的车速。但由于小轿车与二轮摩托车的碰撞属于完全非弹性碰撞，碰撞后两车的速度是相同的，即v_甲=v_乙=v取甲车行驶方向为正x方向，乙车行驶方向与甲车垂直，v_20x=0，则沿甲车行驶方向一个方向动量守恒公式为

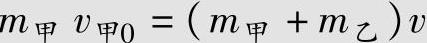
运用类似制动印公式（2-33）计算两车碰撞后的共同速度，为

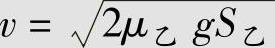
式中，μ_乙为乙车车身刮地滑行的摩擦系数。根据前面的分析，取μ_乙=0.55。S_乙=28.50m，代入上式得

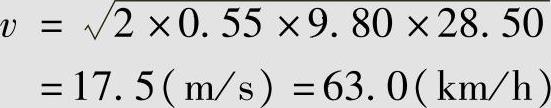
将v值及相关数据代入动量守恒公式，得

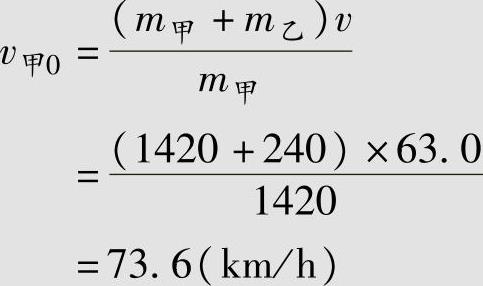
讨论 这个案例与前面【例3-2】是相类似的。但在这里我们利用了汽车与二轮摩托车的碰撞属于完全非弹性碰撞的特性，在汽车没有在路面上留下制动的轮胎印迹的情况下也能求解，而且计算更简单。对于汽车与自行车或行人的碰撞可做类似处理。对于自行车，利用其刮地痕迹，运用类似制动公式计算其刮地滑行的初速度，它也就是汽车碰撞后的车速，因自行车质量很小，可以忽略碰撞对汽车的减速作用，所以实际上这样计算得到的就是汽车在事故发生时的行驶车速。对于行人，在2.6.1节中已经指出，因为汽车与行人的碰撞属于完全非弹性碰撞，利用人体抛出距离计算出的抛出速度，就等于事故发生时汽车的行驶车速。

对于汽车之间的碰撞，利用中速以上汽车碰撞属于或接近完全非弹性碰撞的特点，有时还能帮助车速鉴定人员解决一些特殊的问题。例如两辆高速行驶的汽车相撞，碰撞后其中一辆车与障碍物相撞或翻滚到路外，无法计算其碰撞后的车速。但因为碰撞属于完全非弹性碰撞，只要能够计算出另一辆车碰撞后的速度，它也就代表了两车碰撞后的共同速度。