动量守恒公式在车速鉴定中的应用

以两辆汽车的追尾碰撞为例，运用牛顿定律来推导出动量守恒公式。图3-1所示为质量分别为m₁和m₂的两辆汽车在同向行驶中发生追尾碰撞。碰撞前，两车分别以速度v₁₀和v20互相接近，在发生追尾碰撞的Δt时间内，两车受到来自对方的平均撞击力分别为F₁和F₂，碰撞后两车又分别以速度v₁和v₂相分离。

根据牛顿第二定律，对于两车之间的碰撞，可以分别写出

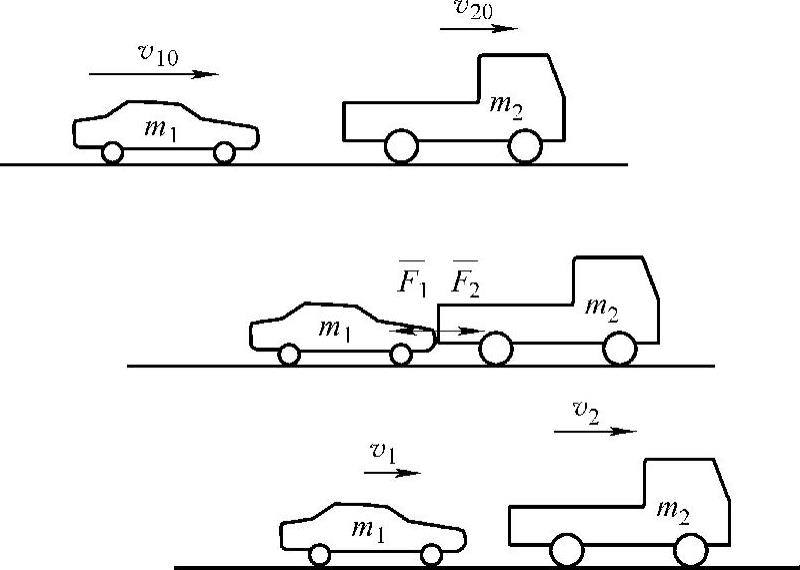
图3-1 两辆汽车的追尾碰撞

式中，F₁和F₂为在Δt时间内两车分别受到对方施加的平均作用力；a₁和a₂为两车在Δt时间内的平均加速度。根据加速度的定义，a表示在Δt时间内速度的平均改变，故

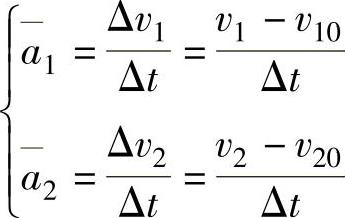
代入式（3-1），得

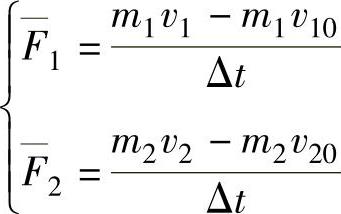
把上式改写为

式中，FΔt称为平均作用力的冲量；mv称为物体的动量。根据牛顿第三定律，两车在任何瞬间相互施加的作用力都是大小相等、方向相反的，所以在Δt时间内的平均值也是如此，由此得

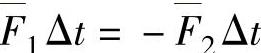
代入式（3-2），得

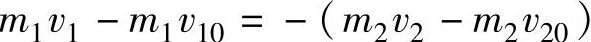
整理得

式(3-3)具有非常重要的意义。它表明，在机动车的碰撞中，不管两车之间相互的撞．击力多么复杂，也不管碰撞持续时间的长短，如果把两车作为一个系统，只要在两车的碰撞过程中除了它们之间的撞击力之外不存在其他外力的作用．则系统碰撞前后动量的总和保持不变。．

式（3-3）是由汽车的追尾碰撞推导出来的，但对于汽车的迎面碰撞同样适用。对于汽车的迎面碰撞，可取其中一辆车的前进方向为正方向，则碰撞前另一辆车的动量取负号。

以上讨论的是在一条直线上运动的机动车碰撞的动量守恒。然而在道路交通事故大多数的碰撞中，机动车的运动并不是在一条直线上，例如机动车的横撞，碰撞前两车行驶方向互相垂直，碰撞后一般也不朝一个方向运动。在这样的情况下，从力学理论可以证明（推导从略），动量守恒仍然成立，但此时动量中的速度要表示为有方向的矢量，用黑体字母v表示。于是，一般形式的动量守恒公式表示为

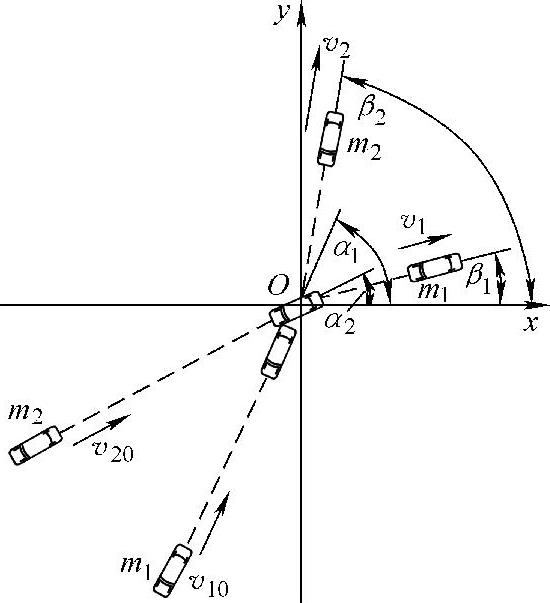
图3-2 小轿车的斜向碰撞(www.xing528.com)

将矢量形式的动量守恒公式应用于道路交通事故的车速鉴定时，需要把两车碰撞前后的动量分别投影到x、y两坐标轴上，从而得出系统沿x、y两个方向动量守恒的分量式。下面以两辆小轿车的斜向碰撞为例来说明如何将动量守恒的分量式应用于车速鉴定。

图3-2所示为两辆质量分别为m₁、m₂的小轿车，在以速度分别为v₁₀和v₂₀行驶中发生斜向碰撞，碰撞后两车速度分别为v₁和v₂。取坐标系O-xy。将两车碰撞前后的动量分别投影到x、y两轴上，则动量守恒表达式（3-4）沿x、y两个方向的分量式为

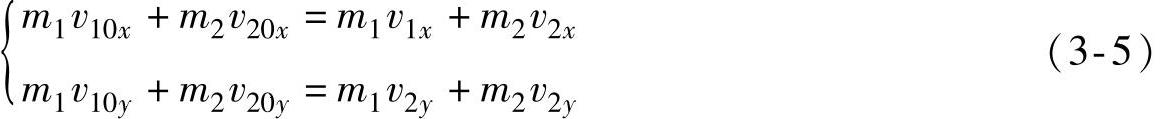
以α₁、α₂和β₁、β₂分别代表碰撞前后v₁₀、v₂₀和v₁、v₂与x轴的夹角，则式（3-5）的实用计算公式为

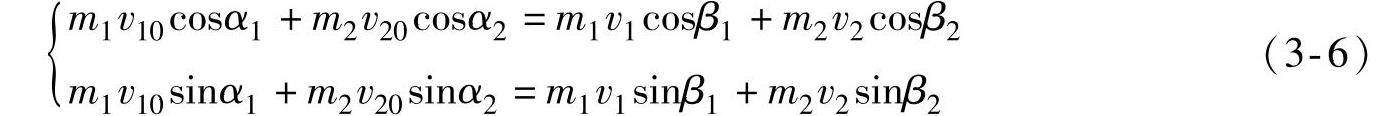
面对重大交通事故错综复杂的现场和受损严重的车辆，不熟悉力学的读者可能会提出疑问：动量守恒真的在这样严重的碰撞事故中还成立吗？从式（3-3）的推导过程我们看到，系统动量守恒的唯一条件是作用于系统的合外力为零．对于由两辆相互碰撞的汽车组成的系统，两车之间的撞击力属于系统的内力，它不影响动量守恒成立。那么，在汽车碰撞过程中是否完全不存在外力呢？也不是都不存在，例如若汽车在碰撞过程中实施了制动，则汽车轮胎与路面的摩擦力就属于作用于系统的外力。但2.2.2节中已经指出，在碰撞事故中，汽车的平均撞击减速度数十倍于重力加速度g，而轮胎与路面摩擦力的减速度a=μg，它小于g，故撞击力数十倍于轮胎与路面的摩擦力。所以，可以说在95%以上的精度内，对于机动车的任何碰撞事故，动量守恒公式都可靠成立。我们再举一些人们在日常生活中熟悉的极端例子：地雷爆炸时，各块碎片间的内力作用是十分剧烈的，但若把地雷作为一个系统，爆炸前后其动量仍保持守恒。爆炸前系统的总动量为零；爆炸后碎片以各种速度向四面八方飞散，但若将所有碎片的动量投影到x、y方向代数相加，其总和必然仍然等于零。节日里礼花在天空中爆炸，其火花外围总是保持一个球形，这就是动量守恒的体现。实际上，动量守恒已经超越了力学的范畴，成为自然界最普遍的基本定律之一。所以，车速鉴定工作者要树立一个明确的概念：不论所碰到的事故是多么复杂、案情多么扑朔迷离．任何时候都不要怀疑动量守恒公式的正确性。动量守恒是碰撞事故车速鉴定最可靠的理论工具。

【例3-1】 一辆质量为m₁=1560kg的小轿车由南向北行驶至交叉路口时，与一辆质量为m₂=1365kg由西向东行驶的小轿车发生横向碰撞，如图3-3所示。碰撞后两车滑行的距离分别为S₁=13.20m和S₂=10.50m，其滑行方向与正东方面的夹角分别为β₁=52.5°和β₂=68.0°。设两车碰撞后均采取了制动措施，求两车在事故发生时的行驶车速。路面性质为干燥沥青路面。

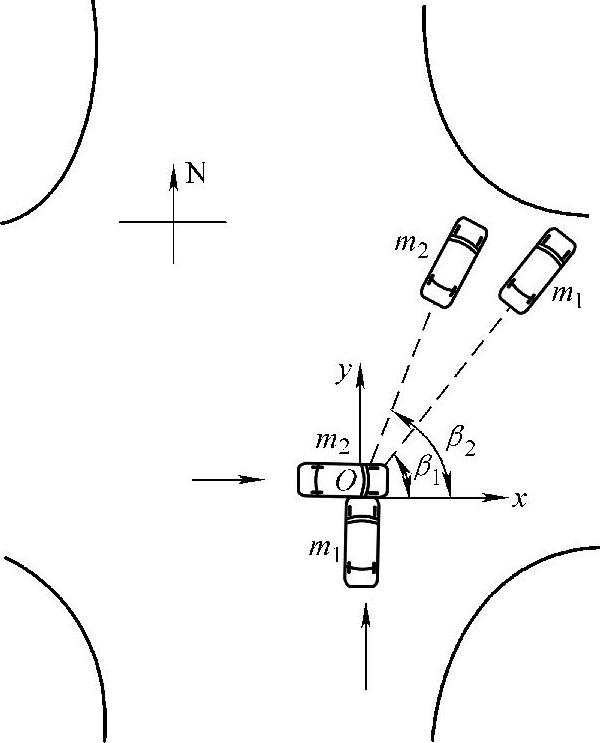
图3-3　例3-1用图

解：取坐标系如图3-3所示，则β₁、β₂就是v₁和v₂与x轴的夹角。根据式（3-6），写出系统沿x、y两个方向的动量守恒公式。考虑到碰撞前1车沿正y方向行驶，其动量在x方向投影为零；2车沿正x方向行驶，其动量在y方向投影为零，于是动量守恒的表达式（3-6）简化为

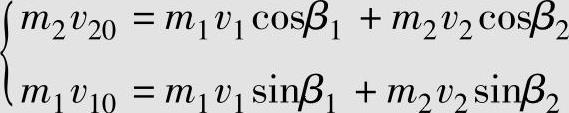
两车碰撞后的速度可分别用制动印公式计算，有

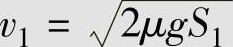
式中，μ为两车轮胎与路面的摩擦系数。小轿车一般配备有ABS，制动性能较好，取μ=0.80，代入相关数据，得

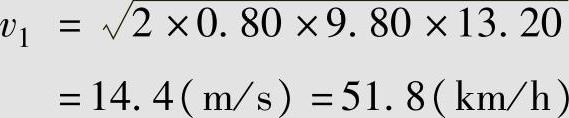
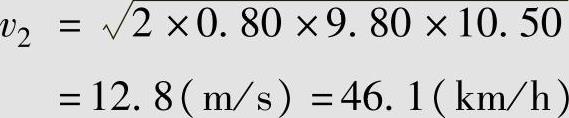
将相关数据代入动量守恒公式

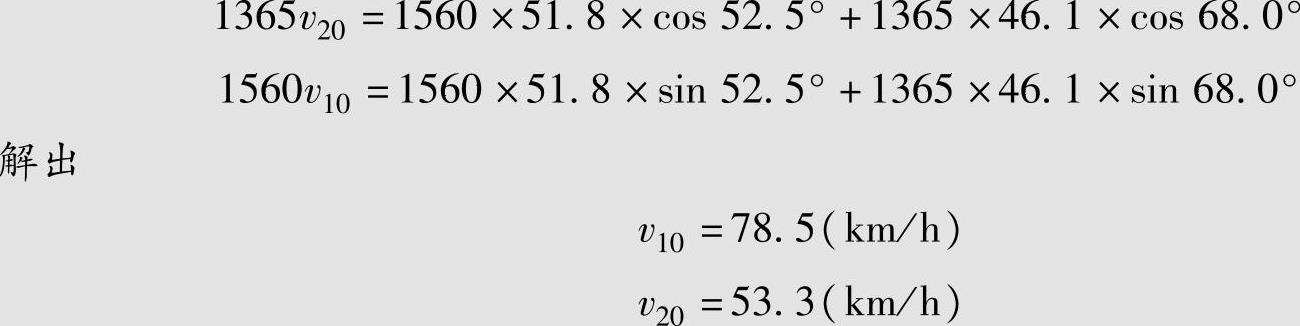
讨论　以上案例充分显示了动量守恒公式应用于机动车碰撞事故所展现出的威力。一个初看起来相当复杂、后果很严重的碰撞事故，我们不用去管撞击力的大小和两车碰撞的形变情况，只需利用现场图提供的两车碰撞点的位置、碰撞后的运动方向和滑行距离等数据，通过列出x、y两个方向的动量守恒分量公式，用两个代数方程求解两个未知数，就可轻松求解车速。

上述案例可能给读者造成一个印象，似乎所有涉及机动车碰撞的事故，都能像这样通过求解x、y两个方向的动量守恒方程得到解决。事实并非如此。在很多情况下，我们无法列出x、y两个方向上的动量守恒公式，而只能列出一个方向的动量守恒公式。例如机动车对心的迎面碰撞或追尾碰撞，碰撞前后机动车的运动大致都在一条直线上，因此我们只能写出式（3-3）那样的一个方向的动量守恒方程。又如，如果是汽车与二轮摩托车发生横向碰撞，虽然从理论上说，我们也能够采用类似【例3-1】的方法，列出x、y两个方向的动量守恒分量式求解，但因摩托车的质量比汽车的小很多，碰撞对汽车行驶方向的改变很小。计算表明，小∙角∙度∙测∙量∙的∙误∙差∙对∙于∙二∙轮∙摩∙托∙车∙的∙车∙速∙计∙算∙结∙果∙影∙响∙很∙大∙；此外考虑到汽车驾驶员在临碰撞前还有可能打方向盘避让，这使汽车运动方向改变角的测量更不准确，从而使这一方法实际不能应用。但是实践表明，对于诸如此类的案例，沿道路纵向或汽车行驶方向一个方向的动量守恒公式，仍然是车速鉴定的可靠理论工具。

总之，在以往大量的车速鉴定实践中，我们能够运用x、y两个方向动量守恒公式解决的案例只占很小一部分，绝大多数的案例都只能列出一个方向的动量守恒公式。于是带来一个问题：一个方向的动量守恒公式中有两个未知数v₁₀和v₂₀，而一个方程不能求解两个未知数。这就要求我们还需要利用其他方法建立第二个包含v₁₀和v₂₀的代数方程，或者设法消去其中一个未知数，否则方程就不可能求解。以下的讨论基本上是围绕这个问题展开的。