甩尾汽车车速计算方法及案例分析

以上试验数据是在特定的试验条件下获得的，而且试验的结果只能够确定若汽车后轮先抱死，当车速超过48km/h时将发生甩尾，而不能确定车速的具体数值，因而不能直接运用于车速计算。

计算汽车在发生甩尾时的行驶车速，就是计算汽车在甩尾滑行过程中轮胎的横向摩擦力对汽车的减速。由于在甩尾过程中横向摩擦力是个变力，汽车不是做匀减速运动，计算很复杂。国外研究者提出了一种近似计算方法^[10]，其推导过程需要运用3.4.1节中功的定义和3.4.2节中的动能定理，对此不熟悉的读者建议在阅读第3章的相关章节后再回过头来阅读这段推导，或干脆略去这段推导直接运用推导出的车速计算公式（2-38）。

设汽车在滑行中因侧向力的作用发生了甩尾，汽车最后停止位置相对原行驶的方向车身转体θ₀角，甩尾滑行的总距离为S₀。近似认为汽车在甩尾中车身的转角与其滑行距离成正比，即

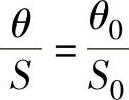
可写成

式中，S和θ分别为汽车在任一瞬间滑行过的距离和车身转过的角度。

在甩尾过程中汽车的横向摩擦系数是一个变量，根据前面的分析，当θ=0时，汽车是在纵向抱死制动的情况下的横滑，轮胎横向摩擦系数接近零；当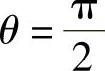，即车身与道路纵向垂直时，汽车为纯粹的横滑，横向摩擦系数达到最大值。当θ=π时，又回归到接近零。图2-16所示为θ从时横向摩擦系数的变化规律，它类似正弦函数的变化规律。于是，可将横向摩擦系数与车身转角的关系表示为

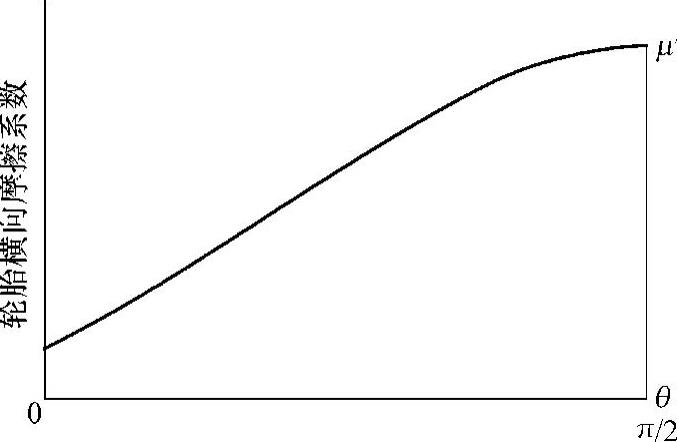
图2-16 横向摩擦系数随车身转角的变化

μ=μ′sinθ（2-36）

式中，μ为转角为θ时的横向摩擦系数；μ′为横向摩擦系数的最大值，可用式（2-33）计算。为计算事故汽车在甩尾时的行驶车速，需要运用第3章的动能定理公式（3-33），当末速为零时表达式为：

式中，v₀为汽车在发生甩尾时的行驶车速；W为汽车在甩尾过程中轮胎与路面横向摩擦力所做的功。设在任一瞬间车身的转角为θ，汽车滑行一段小距离ds时摩擦力所做的元功为

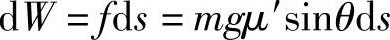
汽车滑行总距离S₀摩擦力所做的总功为(www.xing528.com)

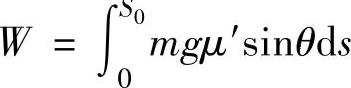
且

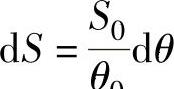
代入得

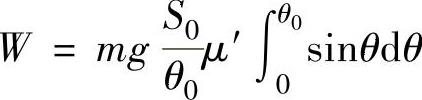
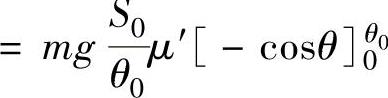
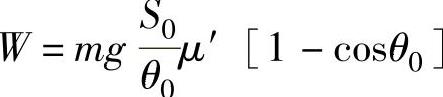
即

将W值代入式（2-36），可解出

式（2-38）在形式上类似制动印公式，只是其中摩擦系数μ要修正为一个随θ₀而变化的量。注意，式（2-38）中θ₀的单位为弧度。实际的甩尾事故是很复杂的，路况不同，侧向作用力的大小不同，情况也会有所差别，式（2-38）不能算是严格的理论公式，只能算是一个实用的近似计算公式。

【例2-12】 一辆小型货车在雨天潮湿的沥青路面上发生甩尾，汽车滑行40.00m距离，转体180°，求该车发生甩尾时的行驶车速。

解：已知θ₀=π，S₀=40.00m，根据表2-2，对于潮湿沥青路面，纵向摩擦系数取值为0.40～0.60，对于货车取中间偏低值，即取μ=0.45，代入式（3-33）得μ′=0.97×0.45+0.08=0.52。将相关数据代入式（2-38），得

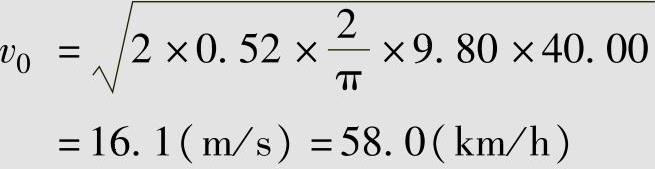
结论 甩尾小型货车事故发生时的行驶车速约为58km/h。