匀变速直线运动-道路交通事故车速鉴定的方法和案例选析

道路交通事故中，许多事故车辆在事故发生过程中的运动都属于匀变速直线运动，例如驾驶员踩制动踏板实施紧急制动、大货车在急转弯中发生侧翻车身刮擦地面运动等。在这些运动中，由于作用在车辆上的力（如摩擦力、重力等）都是恒力，车辆在事故过程中做匀变速直线运动。匀变速直线运动遵循下列规律：

对于匀加速直线运动

对于匀减速直线运动

式中，v为车辆在t时刻的末速度；v₀为初始时刻即t=0的初速度；a为车辆的加速度或减速度（匀加速和匀减速运动的规律已经分开来写，因此不论是运用式（2-1）或式（2-2），a都取正数）；t为车辆做匀变速直线运动的时间；S为t时间内车辆运动的距离。

在道路交通事故中，事故车辆一般做匀减速运动。例如：汽车驾驶员实施紧急制动时，他踩下制动踏板把车轮抱死，车轮由滚动变成滑动，这使轮胎与路面的摩擦力大大增加，由于轮胎与路面的滑动摩擦力是不变的，汽车做匀减速运动直至停止。侧翻的大货车也是如此，由于大货车车身与路面的摩擦阻力，翻倒的大货车在路面上也做匀减速直线运动直至停止。所以在道路交通事故车速鉴定中使用的基本公式是式（2-2），即

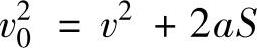
为便于计算，公式改写为

【例2-1】 某肇事汽车驾驶员发现前方行人横过道路后立即实施了紧急制动，但汽车仍与行人发生了碰撞，汽车在制动滑行25.50m距离后停下。事故发生后对肇事汽车进行了车检，用加速仪测得该车“充分发出的平均减速度”a_max=5.85m/s²，求该车在实施紧急制动前的行驶车速。

解：对于汽车与行人的碰撞，由于汽车的质量远大于行人的质量，碰撞对汽车的减速作用可以忽略不计。根据案情，肇事汽车驾驶员在发现险情后立即实施了紧急制动直至最后停止，故末速v=0，制动距离S=25.50m，车检得出的“充分发出的平均减速度”a_max就代表肇事汽车在事故发生过程中制动滑行的减速度，即a=5.85m/s²。将相关数据代入式（2-3），得

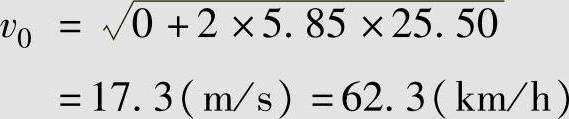
注意(www.xing528.com)

在车速计算公式中，一般都统一使用国际单位制kg、m、s，即质量的单位为千克(kg)，长度单位为米(m)，时间单位为秒(s)。在这一单位制中，速度的单位为米／秒(m／s)；但在车速鉴定中，对于机动车习惯用千米／小时(km/h)作为速度的单位，此时需要乘上一个单位转换系数3.6，它是这样得来的：

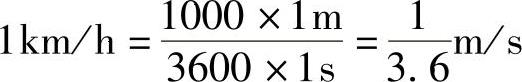
所以有

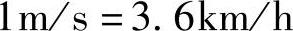
【例2-2】　某小客车在行驶中失控冲出路外坠落山谷，在冲出公路前该车已实施了紧急制动，制动距离为18.20m。已知该车冲出路外瞬间的速度为54.0km/h。事故发生后对已损坏的小客车进行了拆检，车检报告表明该车在发生事故前制动系的性能符合安全标准，制动力合格。求该肇事汽车在事故发生时，即因失控实施紧急制动前的行驶速度。

解：本案中，肇事小客车在冲出路外坠落山谷的瞬间仍有54.0km/h的速度，故应用式（2-3）时末速v≠0，问题是确定减速度的取值。因事故车辆坠落山谷后严重损坏，不能用加速仪测量“充分发出的平均减速度”a_max，但拆检确定该车在坠落山谷前制动性能合格。根据GB7258—2012（表1-1），制动力合格的小客车满载时a_max≥5.9m/s²，空载时a_max≥6.2m/s²，该车满载，取a=6.0m/s²。已知S=18.20m，将相关数据代入式（2-3），得

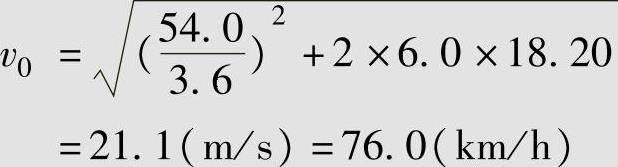
讨论 在以上两个例题的计算中，我们对计算结果都只取了3位有效数字，即62.3km/h和76.0km/h。为什么要这样做呢？因为计算结果能够精确到几位数字，是由计算公式中所包含的已知参数的精确程度决定的，其精确程度表现为参数数字的位数，这个位数称为“有效数字”。例如a_max的测量通常只能精确到3位有效数字，像例2-1中a_max=5.85m/s²，这就表示加速度测量的精确程度只能达到小数点后两位（总有效数字3位）。如果再进行一次测试，则其结果可能变成5.82m/s²，说明小数点后第二位存在误差。理论计算表明，如果一个计算式中所包含参数的有效数字为n，那么通过计算式计算出的结果其有效数字不可能超过n。例如例2-1中若取另一次试验值a_max=5.82m/s²，则有

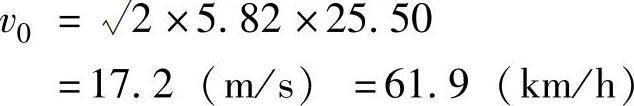
可见，a取值第三位的误差影响到计算结果的第三位，两次计算结果相差0.04km//h，所以在车速计算结果的表达式中取第三位以后更多位数字是没有意义的。例如有的鉴定工作者会把[例2-1]的计算式写成

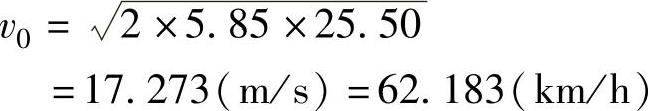
这是不对的。因为上述分析已经表明，由于计算式中参数的精确程度只能达到3位有效数字，计算结果的精确程度也只能达到3位有效数字，既然第三位已经有误差，则第三位以后的数字毫无意义，而且会误导办案人员。通常在车速计算中，计算式中参数取值的有效数字都不超过3位，如长度S=25.50m有4位，其余都不超过3位。如重力加速度g=9.80m/s²，a_max=5.85m/s²，有效数字都是3位。轮胎与路面的摩擦系数有效数字只有两位，如μ=0.63。计算结果的有效数字是由计算式中参数有效数字的最低位数决定的，所以在车速鉴定结果的表达中，一般最多只能取3位有效数字，如v₀=17.3m/s=62.3km/h。